R တွင် ကြံ့ခိုင်မှု အားနည်းခြင်း စမ်းသပ်နည်း (တစ်ဆင့်ပြီးတစ်ဆင့်)

ပြည့်စုံသော ဆုတ်ယုတ်မှုပုံစံ သည် မော်ဒယ်၏လျှော့ချဗားရှင်းထက် ဒေတာအတွဲတစ်ခုနှင့် သိသိသာသာ ပိုမိုကိုက်ညီမှုရှိမရှိကို ဆုံးဖြတ်ရန် ကြံ့ခိုင်မှုစမ်းသပ်မှုအားနည်းခြင်းကို အသုံးပြုသည်။

ဥပမာအားဖြင့်၊ ကောလိပ်တစ်ခုရှိ ကျောင်းသားများအတွက် စာမေးပွဲရမှတ်များကို ခန့်မှန်းရန် လေ့လာခဲ့သည့် နာရီအရေအတွက်ကို အသုံးပြုလိုသည်ဆိုကြပါစို့။ အောက်ဖော်ပြပါ ဆုတ်ယုတ်မှုပုံစံနှစ်ခုကို လိုက်လျောညီထွေဖြစ်အောင် ကျွန်ုပ်တို့ ဆုံးဖြတ်နိုင်သည်-

မော်ဒယ်အပြည့်အစုံ- ရမှတ် = β ₀ + B ₁ (နာရီ) + B ₂ (နာရီ) ²

လျှော့ချထားသော မော်ဒယ်- ရမှတ် = β ₀ + B ₁ (နာရီ)

အောက်ဖော်ပြပါ အဆင့်ဆင့် ဥပမာသည် မော်ဒယ်ပြည့်သည် လျှော့ချထားသော မော်ဒယ်ထက် သိသိသာသာ ပိုမိုကောင်းမွန်သော အံဝင်ခွင်ကျ ဖြစ်မဖြစ်ကို ဆုံးဖြတ်ရန် R တွင် အံဝင်ခွင်ကျ မရှိသော စမ်းသပ်မှုကို မည်သို့ လုပ်ဆောင်ရမည်ကို ပြသထားသည်။

အဆင့် 1- ဒေတာအတွဲတစ်ခုကို ဖန်တီးပြီး မြင်ယောင်ကြည့်ပါ။

ပထမဦးစွာ၊ ကျောင်းသား 50 အတွက် ဖြေဆိုရသည့် နာရီအရေအတွက်နှင့် စာမေးပွဲရမှတ်များပါဝင်သော ဒေတာအတွဲကို ဖန်တီးရန် အောက်ပါကုဒ်ကို အသုံးပြုပါမည်။

 #make this example reproducible
set. seeds (1)

#create dataset
df <- data. frame (hours = runif (50, 5, 15), score=50)
df$score = df$score + df$hours^3/150 + df$hours* runif (50, 1, 2)

#view first six rows of data
head(df)

      hours score
1 7.655087 64.30191
2 8.721239 70.65430
3 10.728534 73.66114
4 14.082078 86.14630
5 7.016819 59.81595
6 13.983897 83.60510

ထို့နောက်၊ နာရီနှင့် ရမှတ်များကြား ဆက်စပ်မှုကို မြင်သာစေရန် အပိုင်းအစတစ်ခုကို ဖန်တီးပါမည်။

 #load ggplot2 visualization package
library (ggplot2)

#create scatterplot
ggplot(df, aes (x=hours, y=score)) +
  geom_point() 

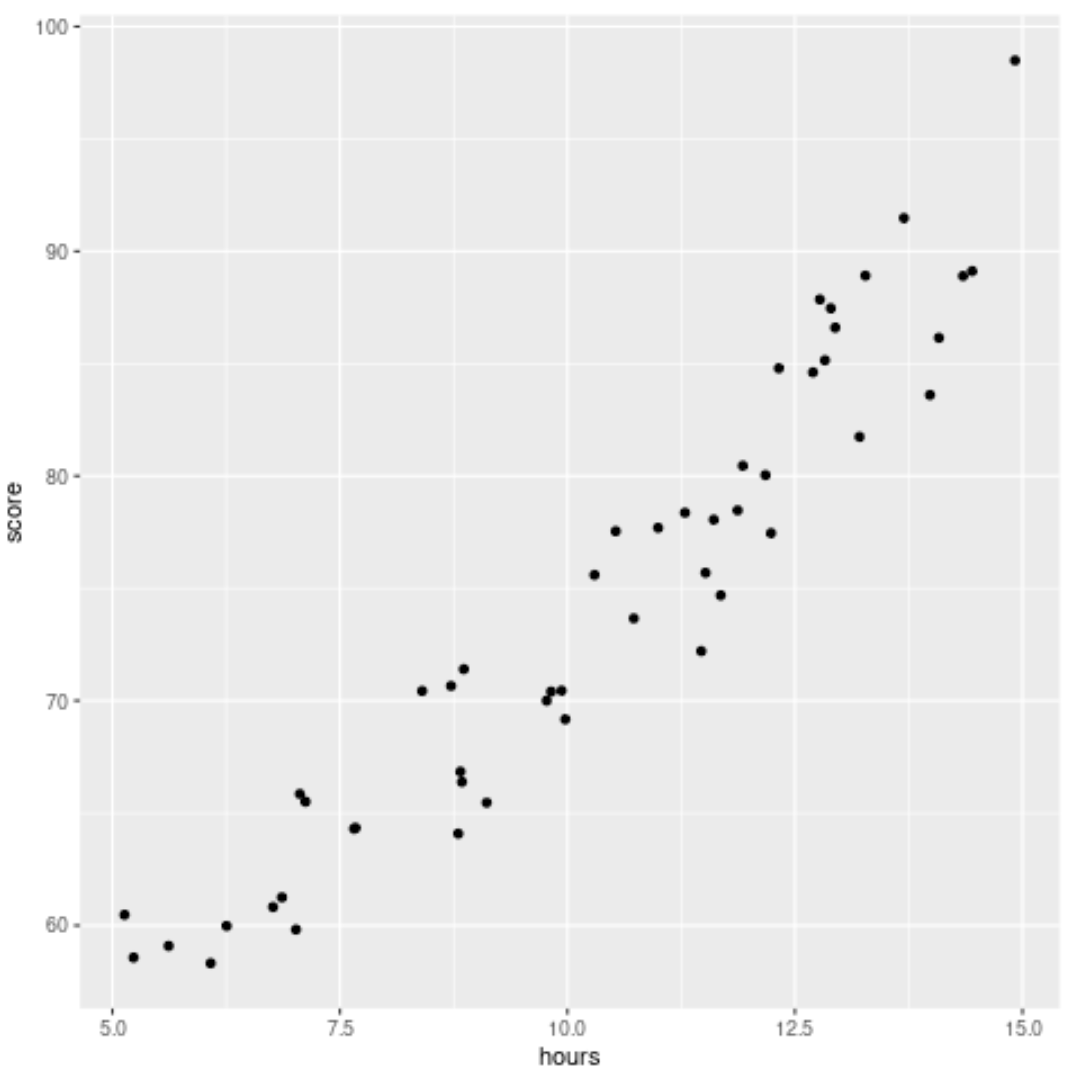
အဆင့် 2- မတူညီသော မော်ဒယ်နှစ်ခုကို ဒေတာအတွဲတွင် တပ်ဆင်ပါ။

ထို့နောက်၊ ကျွန်ုပ်တို့သည် dataset တွင် မတူညီသော ဆုတ်ယုတ်မှုပုံစံနှစ်ခုကို ဖြည့်သွင်းပါမည်။

 #fit full model
full <- lm(score ~ poly (hours,2), data=df)

#fit reduced model
reduced <- lm(score ~ hours, data=df)

အဆင့် 3- ကြံ့ခိုင်မှုမရှိသော စမ်းသပ်မှုတစ်ခုကို လုပ်ဆောင်ပါ။

ထို့နောက်၊ ကျွန်ုပ်တို့သည် မော်ဒယ်နှစ်ခုကြားတွင် အံဝင်ခွင်ကျမရှိသော စမ်းသပ်မှုကို လုပ်ဆောင်ရန် anova() အမိန့်ကို အသုံးပြုပါမည်။

 #lack of fit test
anova(full, reduced)

Analysis of Variance Table

Model 1: score ~ poly(hours, 2)
Model 2: score ~ hours
  Res.Df RSS Df Sum of Sq F Pr(>F)   
1 47 368.48                                
2 48 451.22 -1 -82.744 10.554 0.002144 **
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

F test statistic သည် 10.554 ဖြစ်သွားပြီး သက်ဆိုင်ရာ p-value သည် 0.002144 ဖြစ်သည်။ ဤ p-value သည် 0.05 ထက်နည်းသောကြောင့်၊ ကျွန်ုပ်တို့သည် စမ်းသပ်မှု၏ null hypothesis ကို ငြင်းပယ်နိုင်ပြီး မော်ဒယ်အပြည့်အစုံသည် လျှော့ချထားသော model ထက် ကိန်းဂဏန်းအရ သိသာထင်ရှားစွာ ပိုမိုကိုက်ညီမှုရှိကြောင်း ကောက်ချက်ချနိုင်ပါသည်။

အဆင့် 4- နောက်ဆုံးပုံစံကို မြင်ယောင်ကြည့်ပါ။

နောက်ဆုံးတွင်၊ မူရင်းဒေတာအတွဲနှင့် နောက်ဆုံးပုံစံ (မော်ဒယ်အပြည့်အစုံ) ကို မြင်ယောင်နိုင်သည်-

 ggplot(df, aes (x=hours, y=score)) + 
          geom_point() +
          stat_smooth(method=' lm ', formula = y ~ poly (x,2), size = 1) + 
          xlab(' Hours Studied ') +
          ylab(' Score ') 

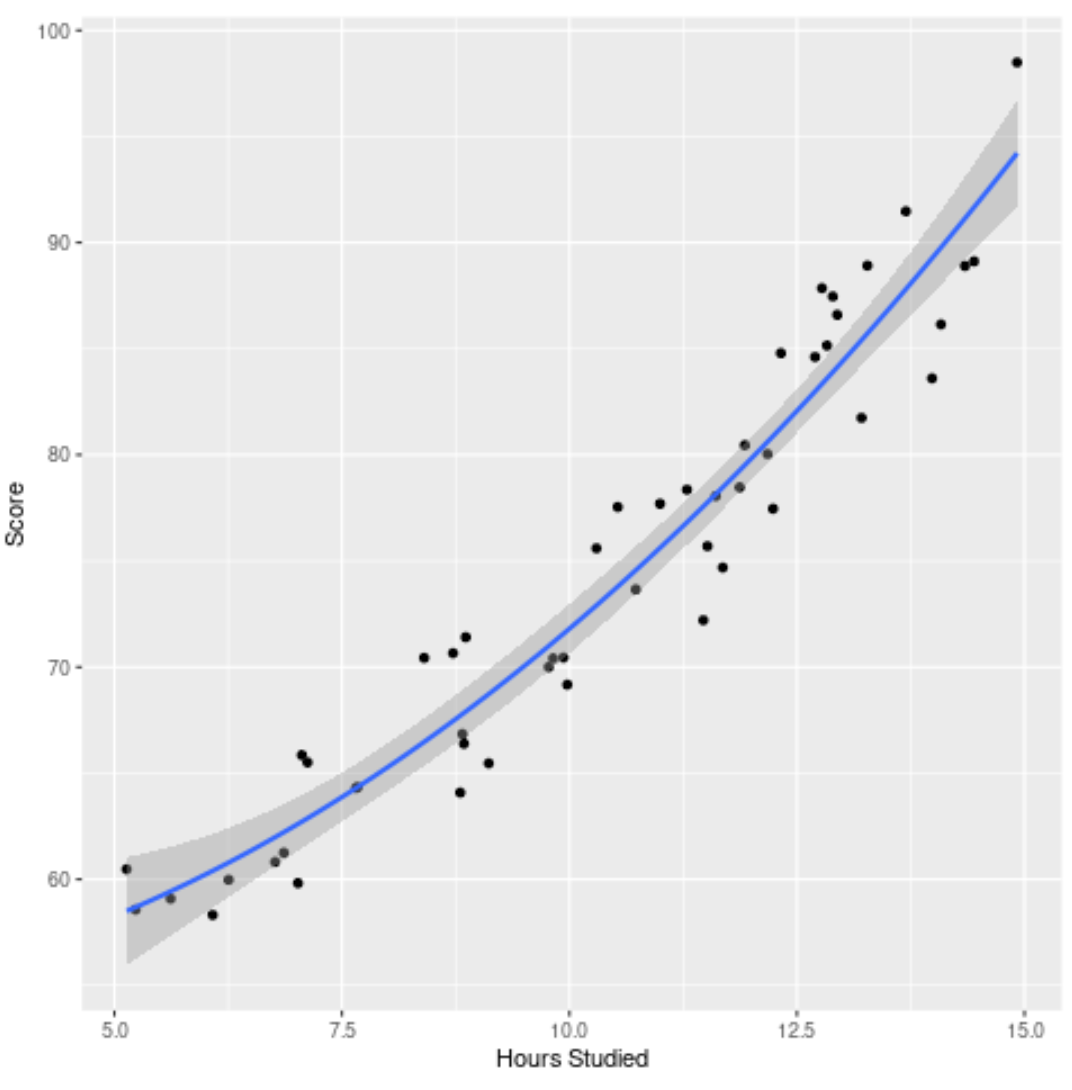
မော်ဒယ်မျဉ်းကွေးသည် ဒေတာနှင့် အလွန်ကိုက်ညီကြောင်း ကျွန်ုပ်တို့မြင်နိုင်သည်။

ထပ်လောင်းအရင်းအမြစ်များ

R တွင် ရိုးရှင်းသော linear regression လုပ်နည်း
R တွင် linear regression အများအပြားလုပ်ဆောင်နည်း
R တွင် polynomial regression ကို မည်သို့လုပ်ဆောင်ရမည်နည်း