Linear မော်ဒယ်များနှင့် ကိုက်ညီစေရန် r တွင် lm() လုပ်ဆောင်ချက်ကို မည်သို့အသုံးပြုရမည်နည်း။

R ရှိ lm() လုပ်ဆောင်ချက်ကို linear regression မော်ဒယ်များနှင့် ကိုက်ညီရန် အသုံးပြုသည်။

ဤလုပ်ဆောင်ချက်သည် အောက်ပါအခြေခံ syntax ကိုအသုံးပြုသည်-

lm(ဖော်မြူလာ၊ ဒေတာ၊ …)

ရွှေ-

• ဖော်မြူလာ- linear model ဖော်မြူလာ (ဥပမာ y ~ x1 + x2)
• ဒေတာ- ဒေတာပါရှိသော ဒေတာဘလောက်၏ အမည်

အောက်ပါနမူနာသည် အောက်ပါအတိုင်းလုပ်ဆောင်ရန် R တွင် ဤလုပ်ဆောင်ချက်ကို အသုံးပြုနည်းကို ပြသသည်-

• ဆုတ်ယုတ်မှုပုံစံကို ကွက်တိပါ။
• ဆုတ်ယုတ်မှုပုံစံ အကျဉ်းချုပ်ကို ကြည့်ပါ။
• မော်ဒယ်ရောဂါရှာဖွေရေးကွက်များကို ကြည့်ပါ။
• တပ်ဆင်ထားသော ဆုတ်ယုတ်မှုပုံစံကို ပုံဖော်ပါ။
• ဆုတ်ယုတ်မှုပုံစံကို အသုံးပြု၍ ခန့်မှန်းချက်များကို ပြုလုပ်ပါ။

ဆုတ်ယုတ်မှုပုံစံကို အံကိုက်ပါ။

R တွင် linear regression model တစ်ခုနှင့်ကိုက်ညီရန် lm() function ကိုအသုံးပြုပုံကို အောက်ပါကုဒ်က ပြသသည် ။

 #define data
df = data. frame (x=c(1, 3, 3, 4, 5, 5, 6, 8, 9, 12),
                y=c(12, 14, 14, 13, 17, 19, 22, 26, 24, 22))

#fit linear regression model using 'x' as predictor and 'y' as response variable
model <- lm(y ~ x, data=df)

ဆုတ်ယုတ်မှုပုံစံအကျဉ်းချုပ်ကို ပြပါ။

ထို့နောက် ကျွန်ုပ်တို့သည် ဆုတ်ယုတ်မှုပုံစံ၏ အကျဉ်းချုပ်ကို ပြသရန် summary() လုပ်ဆောင်ချက်ကို အသုံးပြုနိုင်သည်။

 #view summary of regression model
summary(model)

Call:
lm(formula = y ~ x, data = df)

Residuals:
    Min 1Q Median 3Q Max 
-4.4793 -0.9772 -0.4772 1.4388 4.6328 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 11.1432 1.9104 5.833 0.00039 ***
x 1.2780 0.2984 4.284 0.00267 ** 
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.929 on 8 degrees of freedom
Multiple R-squared: 0.6964, Adjusted R-squared: 0.6584 
F-statistic: 18.35 on 1 and 8 DF, p-value: 0.002675

ဤသည်မှာ မော်ဒယ်ရှိ အရေးကြီးဆုံးတန်ဖိုးများကို အဓိပ္ပာယ်ဖွင့်ဆိုပုံဖြစ်သည်-

• F-statistic = 18.35၊ သက်ဆိုင်ရာ p-value = 0.002675။ ဤ p-value သည် 0.05 ထက်နည်းသောကြောင့်၊ မော်ဒယ်တစ်ခုလုံးသည် ကိန်းဂဏန်းအရ သိသာထင်ရှားပါသည်။
• Multiple R နှစ်ထပ်ကိန်း = 0.6964။ တုံ့ပြန်မှုကိန်းရှင်တွင် ကွဲလွဲမှု 69.64% ကို y ကို ခန့်မှန်းသည့်ကိန်းရှင် x ဖြင့် ရှင်းပြနိုင်သည်ဟု ၎င်းကဆိုသည်။
• ခန့်မှန်းကိန်း x : 1.2780။ ၎င်းသည် x တွင် ထပ်တိုးယူနစ်တစ်ခုစီသည် y တွင် ပျမ်းမျှ 1.2780 တိုးလာခြင်းနှင့် ဆက်စပ်နေကြောင်း ကျွန်ုပ်တို့ကိုပြောပြသည်။

ထို့နောက် ခန့်မှန်းခြေဆုတ်ယုတ်မှုညီမျှခြင်းကို ရေးသားရန် အထွက်မှကိန်းဂဏန်းခန့်မှန်းချက်ကို ကျွန်ုပ်တို့အသုံးပြုနိုင်သည်-

y = 11.1432 + 1.2780*(x)

အပိုဆု – R တွင် ဆုတ်ယုတ်မှုအထွက်တန်ဖိုးတစ်ခုစီကို ဘာသာပြန်ရန် လမ်းညွှန်ချက်အပြည့်အစုံကို ဤနေရာတွင် ရှာတွေ့နိုင်ပါသည်။

မော်ဒယ်ရောဂါရှာဖွေရေးကွက်များကို ကြည့်ပါ။

ထို့နောက် ကျွန်ုပ်တို့သည် ဆုတ်ယုတ်မှုပုံစံ၏ ရောဂါရှာဖွေရေးကွက်များကို စီစဉ်ရန် plot() လုပ်ဆောင်ချက်ကို အသုံးပြုနိုင်သည်။

 #create diagnostic plots
plot(model) 

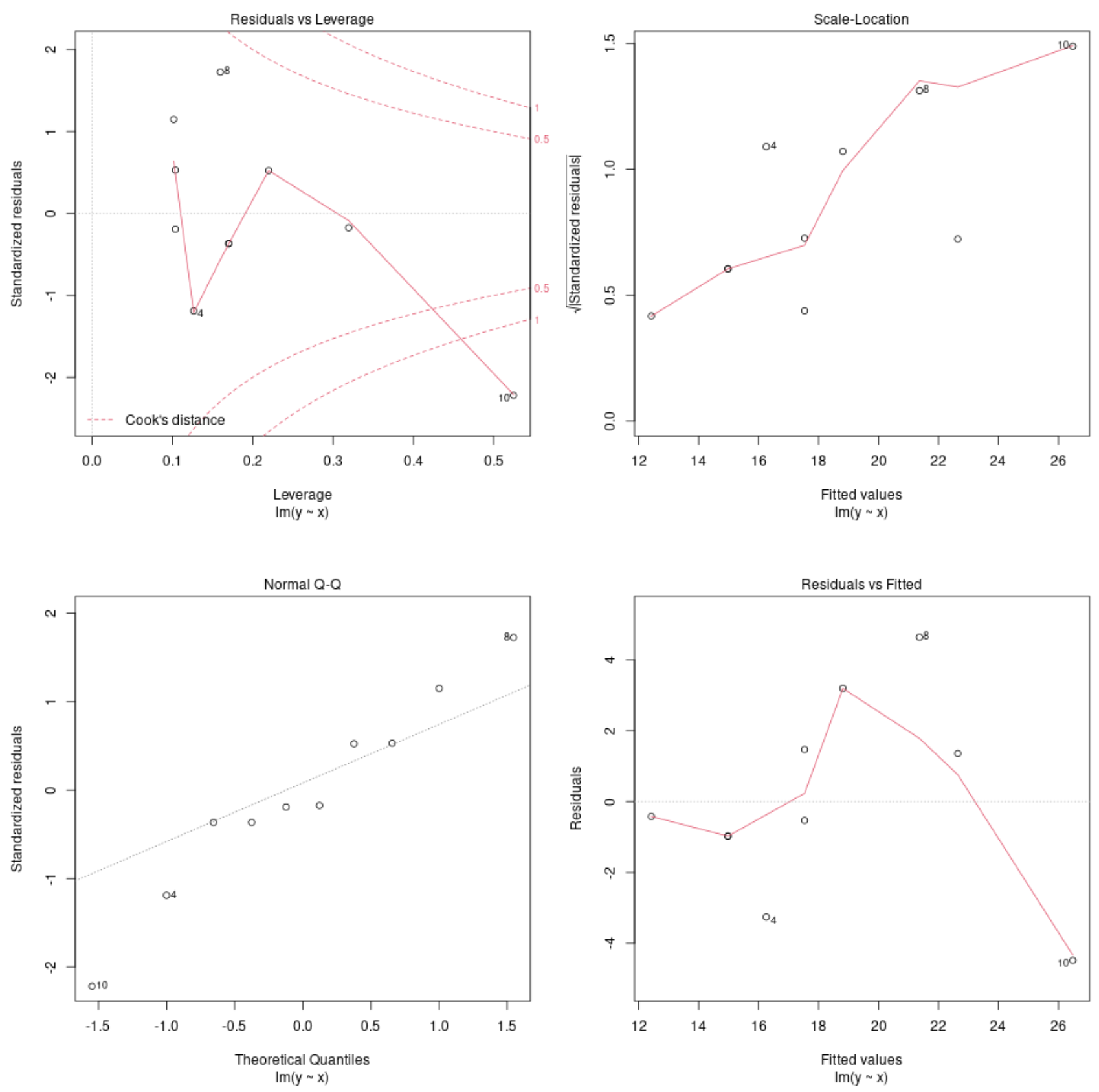
ဤဂရပ်များသည် ဒေတာအတွက် အသုံးပြုရန် သင့်လျော်မှု ရှိ၊ မရှိ ဆုံးဖြတ်ရန် ဆုတ်ယုတ်မှု မော်ဒယ်၏ အကြွင်းအကျန်များကို ပိုင်းခြားစိတ်ဖြာနိုင်စေပါသည်။

R တွင် မော်ဒယ်တစ်ဦး၏ ရောဂါရှာဖွေရေးကွက်များကို အနက်ပြန်ဆိုရန် အပြည့်အစုံ ရှင်းလင်းချက်အတွက် ဤသင်ခန်းစာကို ကြည့်ပါ။

တပ်ဆင်ထားသော ဆုတ်ယုတ်မှုပုံစံကို ပုံဖော်ပါ။

တပ်ဆင်ထားသော ဆုတ်ယုတ်မှုပုံစံကို ကြံစည်ရန် abline() လုပ်ဆောင်ချက်ကို ကျွန်ုပ်တို့ အသုံးပြုနိုင်သည်။

 #create scatterplot of raw data
plot(df$x, df$y, col=' red ', main=' Summary of Regression Model ', xlab=' x ', ylab=' y ')

#add fitted regression line
abline(model)

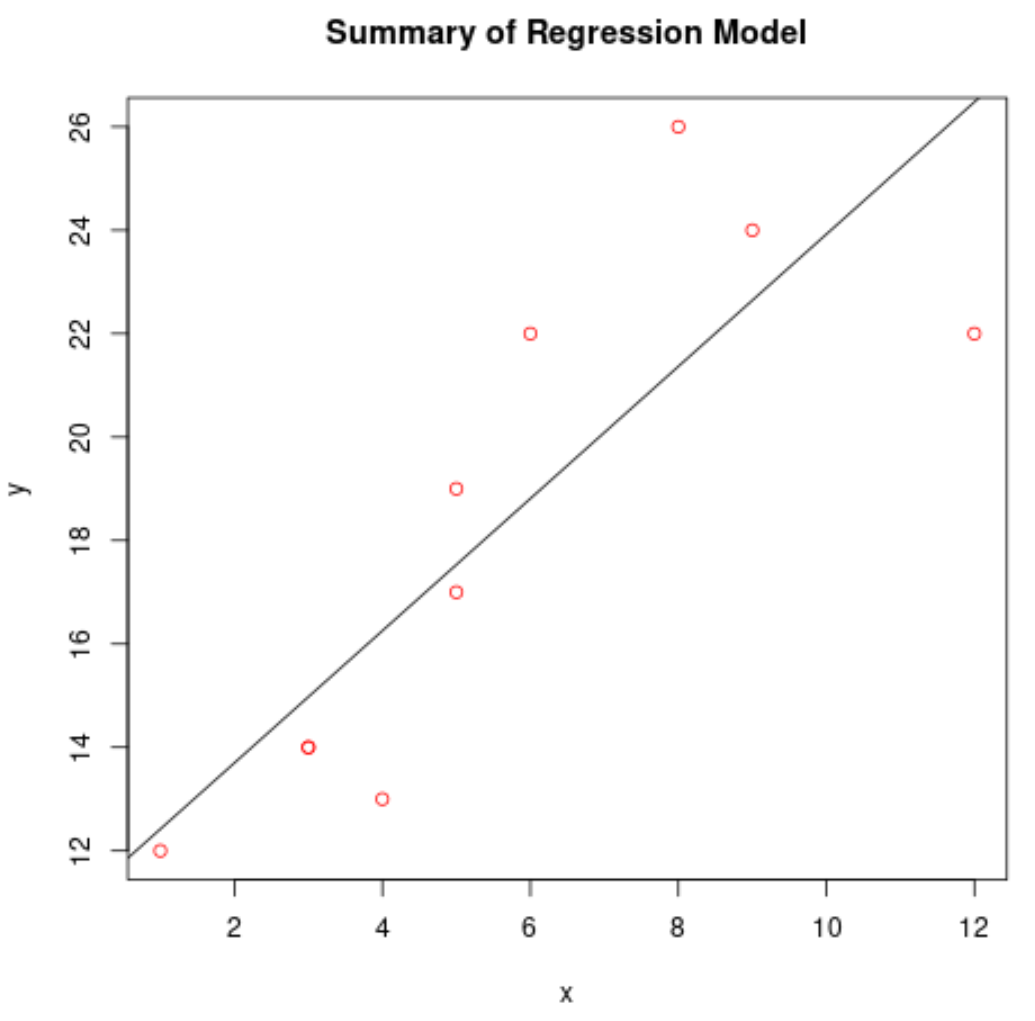
ခန့်မှန်းချက်များကို ပြုလုပ်ရန် ဆုတ်ယုတ်မှုပုံစံကို အသုံးပြုပါ။

လေ့လာမှုအသစ်တစ်ခုအတွက် တုံ့ပြန်မှုတန်ဖိုးကို ခန့်မှန်းရန် ကြိုတင်ခန့်မှန်း() လုပ်ဆောင်ချက်ကို ကျွန်ုပ်တို့အသုံးပြုနိုင်သည်-

 #define new observation
new <- data. frame (x=c(5))

#use the fitted model to predict the value for the new observation
predict(model, newdata = new)

      1 
17.5332

မော်ဒယ်သည် ဤလေ့လာချက်အသစ်တွင် တုံ့ပြန်မှုတန်ဖိုး 17.5332 ရှိမည်ဟု ခန့်မှန်းထားသည်။

ထပ်လောင်းအရင်းအမြစ်များ

R တွင် ရိုးရှင်းသော linear regression လုပ်နည်း
R တွင် linear regression အများအပြားလုပ်ဆောင်နည်း
R တွင် stepwise regression လုပ်နည်း