R တွင် လော့ဂရစ်သမ်ဆုတ်ယုတ်မှု (တစ်ဆင့်ပြီးတစ်ဆင့်)

လော့ဂရစ်သမ် ဆုတ်ယုတ်မှု သည် ပထမပိုင်းတွင် လျင်မြန်စွာ ကြီးထွားမှု သို့မဟုတ် ကျဆင်းမှု အရှိန်မြှင့်ပြီးနောက် အချိန်ကြာလာသည်နှင့်အမျှ နှေးကွေးသည့် အခြေအနေများကို စံနမူနာပြုရန် အသုံးပြုသည့် ဆုတ်ယုတ်မှု အမျိုးအစားတစ်ခု ဖြစ်သည်။

ဥပမာအားဖြင့်၊ အောက်ပါဂရပ်သည် လော့ဂရစ်သမ် ပျက်စီးခြင်း၏ ဥပမာကို ပြသည်-

ဤအခြေအနေမျိုးအတွက်၊ ကြိုတင်ခန့်မှန်းကိန်းရှင်တစ်ခုနှင့် တုံ့ပြန်မှုကိန်းရှင်ကြားရှိ ဆက်နွယ်မှုကို လော့ဂရစ်သမ်ဆုတ်ယုတ်မှုအသုံးပြု၍ ကောင်းစွာစံနမူနာပြုနိုင်သည်။

လော့ဂရစ်သမ် ဆုတ်ယုတ်မှုပုံစံအတွက် ညီမျှခြင်းသည် အောက်ပါပုံစံဖြစ်သည်။

y = a + b*ln(x)

ရွှေ-

• y- တုံ့ပြန်မှု ကိန်းရှင်
• x- ကြိုတင်ခန့်မှန်းနိုင်သောကိန်းရှင်
• a, b- x နှင့် y အကြား ဆက်နွယ်မှုကို ဖော်ပြသည့် ဆုတ်ယုတ်မှုကိန်းဂဏန်းများ

အောက်ဖော်ပြပါ အဆင့်ဆင့် ဥပမာသည် R တွင် လော့ဂရစ်သမ်ဆုတ်ယုတ်မှုကို မည်သို့လုပ်ဆောင်ရမည်ကို ပြသထားသည်။

အဆင့် 1: ဒေတာကိုဖန်တီးပါ။

ပထမဦးစွာ၊ x နှင့် y ကိန်းရှင်နှစ်ခုအတွက် ဒေတာအတုဖန်တီးကြပါစို့။

 x=1:15

y=c(59, 50, 44, 38, 33, 28, 23, 20, 17, 15, 13, 12, 11, 10, 9.5)

အဆင့် 2- ဒေတာကို မြင်ယောင်ကြည့်ပါ။

ထို့နောက် x နှင့် y အကြား ဆက်နွယ်မှုကို မြင်သာစေရန် အမြန် scatterplot တစ်ခုကို ဖန်တီးကြပါစို့။

 plot(x, y) 

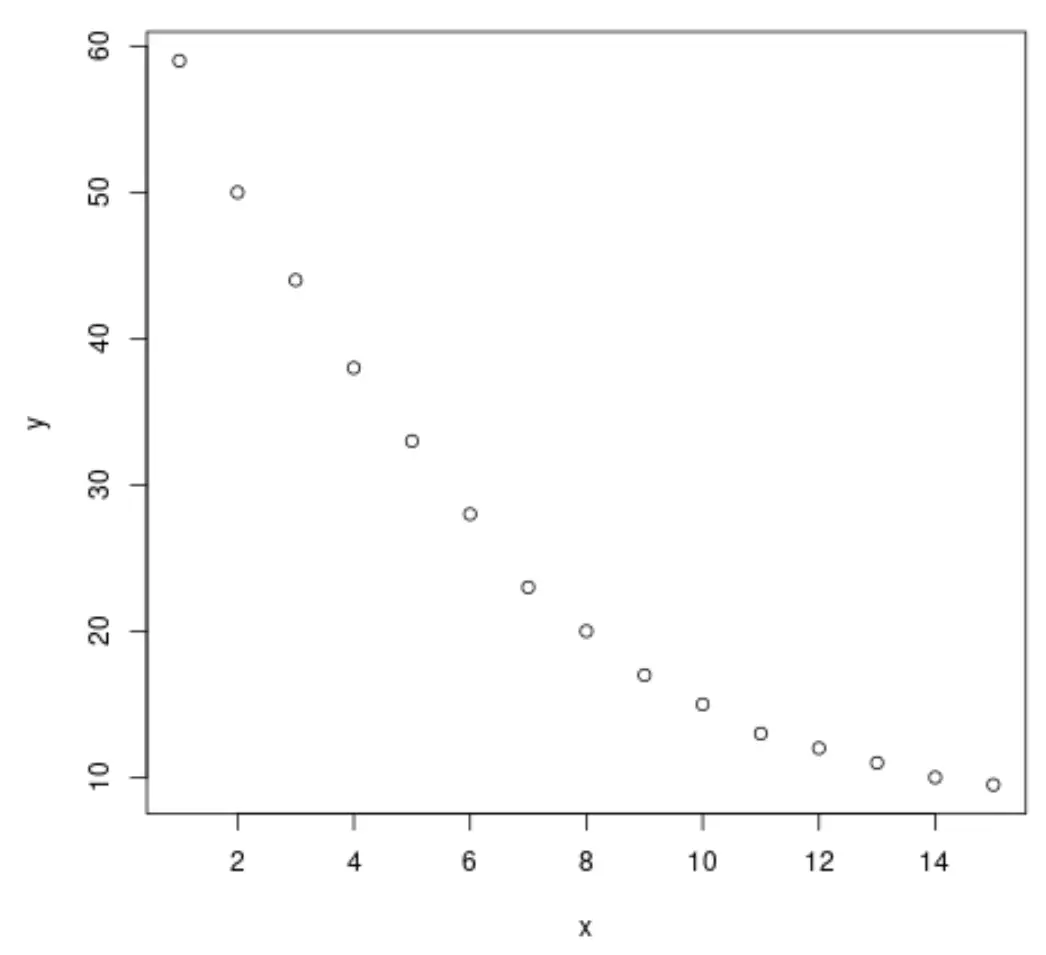
ဂရပ်မှ၊ ကိန်းရှင်နှစ်ခုကြားတွင် ရှင်းလင်းသော logarithmic decay ပုံစံရှိကြောင်း ကျွန်ုပ်တို့တွေ့နိုင်သည်။ တုံ့ပြန်မှုကိန်းရှင် y ၏တန်ဖိုးသည် အစပိုင်းတွင် လျင်မြန်စွာ ကျဆင်းသွားပြီး အချိန်နှင့်အမျှ နှေးကွေးသွားသည်။

ထို့ကြောင့် ကိန်းရှင်များကြား ဆက်နွယ်မှုကို ဖော်ပြရန် လော့ဂရစ်သမ် ဆုတ်ယုတ်မှုညီမျှခြင်းကို အံဝင်ခွင်ကျဖြစ်ဟန်တူသည်။

အဆင့် 3- လော့ဂရစ်သမ်ဆုတ်ယုတ်မှုပုံစံကို အံကိုက်လုပ်ပါ။

ထို့နောက်၊ ကျွန်ုပ်တို့သည် x ၏ သဘာဝ လော့ဂရစ်သမ်ကို ခန့်မှန်းသူကိန်းရှင်နှင့် တုံ့ပြန်မှုကိန်းရှင်အဖြစ် y ကို အသုံးပြု၍ လော့ဂရစ်သမ်ဆုတ်ယုတ်မှုပုံစံနှင့် ကိုက်ညီရန် lm() လုပ်ဆောင်ချက်ကို အသုံးပြုပါမည်။

 #fit the model
model <- lm(y ~ log (x))

#view the output of the model
summary(model)

Call:
lm(formula = y ~ log(x))

Residuals:
   Min 1Q Median 3Q Max 
-4.069 -1.313 -0.260 1.127 3.122 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 63.0686 1.4090 44.76 1.25e-15 ***
log(x) -20.1987 0.7019 -28.78 3.70e-13 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.054 on 13 degrees of freedom
Multiple R-squared: 0.9845, Adjusted R-squared: 0.9834 
F-statistic: 828.2 on 1 and 13 DF, p-value: 3.702e-13

မော်ဒယ်၏ အလုံးစုံ F-တန်ဖိုး သည် 828.2 ဖြစ်ပြီး သက်ဆိုင်သော p-တန်ဖိုးသည် အလွန်နိမ့်နေပါသည် (3.702e-13)၊ မော်ဒယ်တစ်ခုလုံးသည် အသုံးဝင်ကြောင်း ညွှန်ပြပါသည်။

output table မှ coefficients ကို အသုံးပြု၍ တပ်ဆင်ထားသော logarithmic regression equation သည်-

y = 63.0686 – 20.1987 * ln(x)

ကြိုတင်ခန့်မှန်းကိန်းရှင် ကိန်းရှင် x ၏တန်ဖိုးအပေါ်အခြေခံ၍ တုံ့ပြန်မှုကိန်းရှင် y ကို ခန့်မှန်းရန် ဤညီမျှခြင်းကို ကျွန်ုပ်တို့အသုံးပြုနိုင်ပါသည်။ ဥပမာ x = 12 ဆိုရင် y က 12.87 ဖြစ်မယ် ၊

y = 63.0686 – 20.1987 * ln(12) = 12.87

အပိုဆု- ပေးထားသော ခန့်မှန်းသူနှင့် တုံ့ပြန်မှု variable အတွက် လော့ဂရစ်သမ် ဆုတ်ယုတ်မှုညီမျှခြင်းကို အလိုအလျောက် တွက်ချက်ရန် ဤအွန်လိုင်း လော့ဂရစ်သမ် ဆုတ်ယုတ်မှုဂဏန်းတွက်စက်ကို အသုံးပြုပါ။

အဆင့် 4- လော့ဂရစ်သမ်ဆုတ်ယုတ်မှုပုံစံကို မြင်ယောင်ကြည့်ပါ။

နောက်ဆုံးတွင်၊ logarithmic regression model သည် data နှင့်မည်မျှကိုက်ညီကြောင်း မြင်သာစေရန် အမြန်ဂရပ်တစ်ခုကို ဖန်တီးနိုင်သည်-

 #plot x vs. y
plot(x, y)

#define x-values to use for regression line
x=seq(from= 1 , to= 15 , length. out = 1000 )

#use the model to predict the y-values based on the x-values
y=predict(model,newdata=list(x=seq(from= 1 ,to= 15 ,length. out = 1000 )),
          interval=" confidence ")

#add the fitted regression line to the plot (lwd specifies the width of the line)
matlines(x,y, lwd= 2 )

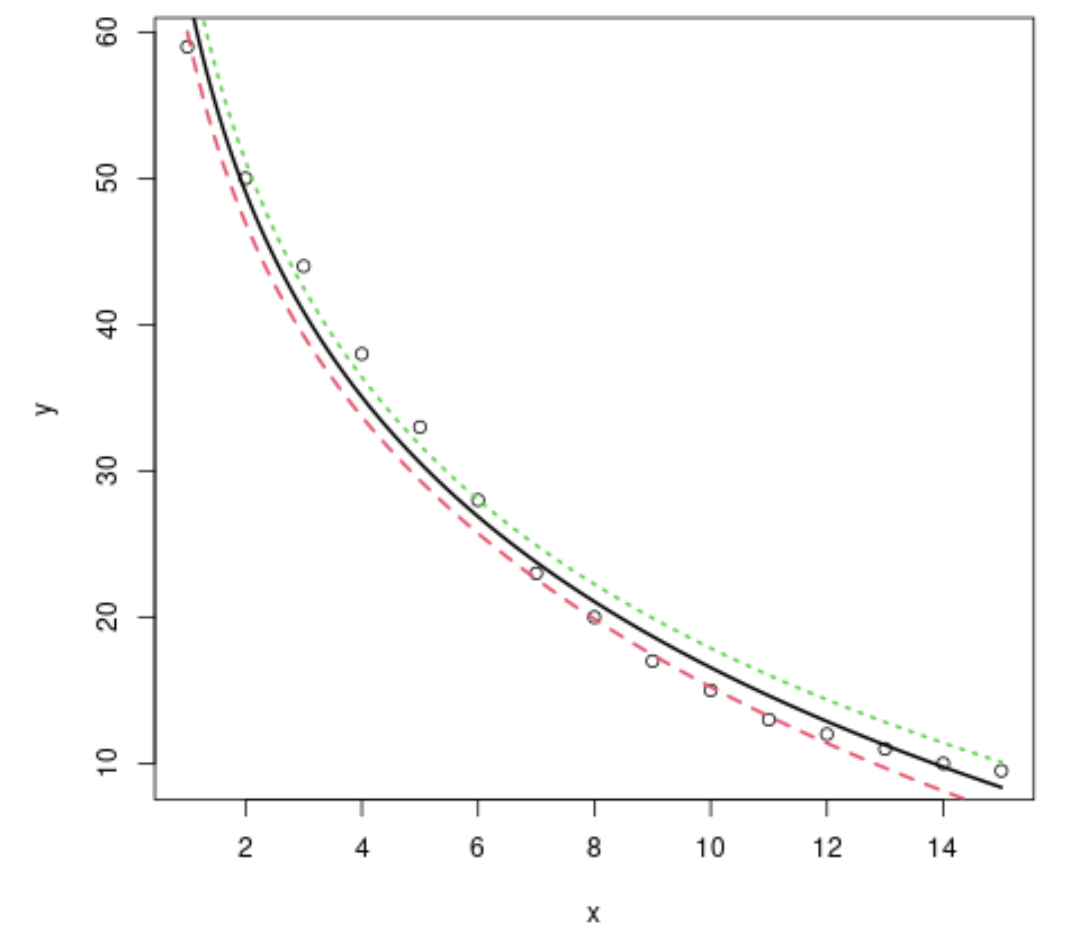
လော့ဂရစ်သမ် ဆုတ်ယုတ်မှုပုံစံသည် ဤအထူးသဖြင့် ဒေတာအစုံနှင့် အံဝင်ခွင်ကျဖြစ်စေသော အလုပ်ဖြစ်သည်ကို ကျွန်ုပ်တို့တွေ့မြင်နိုင်ပါသည်။

ထပ်လောင်းအရင်းအမြစ်များ

R တွင် ရိုးရှင်းသော linear regression လုပ်နည်း
R တွင် linear regression အများအပြားလုပ်ဆောင်နည်း
R တွင် quadratic regression ကို မည်သို့လုပ်ဆောင်ရမည်နည်း။
R တွင် exponential regression လုပ်ဆောင်နည်း
R တွင် polynomial regression ကို မည်သို့လုပ်ဆောင်ရမည်နည်း