R တွင် matthews ဆက်စပ်ကိန်းကို တွက်နည်း

Matthews Correlation Coefficient (MCC) သည် အမျိုးအစားခွဲခြင်းပုံစံ တစ်ခု၏ စွမ်းဆောင်ရည်ကို အကဲဖြတ်ရန် ကျွန်ုပ်တို့အသုံးပြုနိုင်သည့် မက်ထရစ်တစ်ခုဖြစ်သည်။

အောက်ပါအတိုင်း တွက်ချက်သည်။

MCC = (TP*TN – FP*FN) / √ (TP+FP)(TP+FN)(TN+FP)(TN+FN)

ရွှေ-

• TP : စစ်မှန်သော အပြုသဘောဆောင်သည့် အရေအတွက်
• TN : အနုတ်အမှန် အရေအတွက်
• FP : မှားယွင်းသော အပြုသဘောဆောင်သည့် အရေအတွက်
• FN : မှားယွင်းသော အနုတ်လက္ခဏာ အရေအတွက်

အတန်းနှစ်ခုသည် ဟန်ချက်မညီသောအခါတွင် ဤမက်ထရစ်သည် အထူးသဖြင့် အသုံးဝင်သည်၊ ဆိုလိုသည်မှာ အတန်းတစ်ခုသည် အခြားတစ်ခုထက် များစွာပိုနေပါသည်။

MCC ၏တန်ဖိုးသည် -1 နှင့် 1 အကြားတွင် ရှိနေသည်-

• -1 သည် ခန့်မှန်းထားသော အတန်းများနှင့် အမှန်တကယ် အတန်းများကြား သဘောထားကွဲလွဲမှုကို ညွှန်ပြသည်။
• ဘ၀ ဟူသည် လုံးဝ ကြုံသလို မှန်းဆခြင်း ဖြစ်သည်။
• 1 သည် ခန့်မှန်းထားသော အတန်းများနှင့် အမှန်တကယ် အတန်းများကြား ပြီးပြည့်စုံသော သဘောတူညီချက်ကို ညွှန်ပြသည်။

ဥပမာအားဖြင့်၊ အားကစားသုံးသပ်သူတစ်ဦးသည် မတူညီသောကောလိပ်ဘတ်စကက်ဘောကစားသမား 400 ကို NBA သို့ ရေးဆွဲမည်လား မခန့်မှန်းရန် ထောက်ပံ့ပို့ဆောင်ရေးဆုတ်ယုတ်မှုပုံစံကို အသုံးပြုသည်ဆိုပါစို့။

အောက်ဖော်ပြပါ ရှုပ်ထွေးမှု matrix သည် မော်ဒယ်မှ ပြုလုပ်သော ခန့်မှန်းချက်များကို အကျဉ်းချုပ်ဖော်ပြသည်-

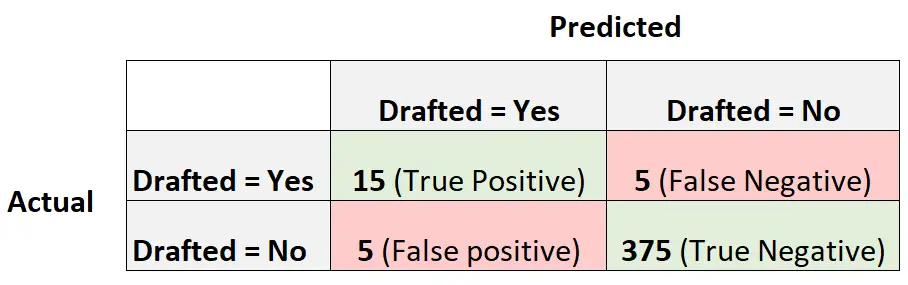
မော်ဒယ်၏ MCC ကိုတွက်ချက်ရန်၊ ကျွန်ုပ်တို့သည် အောက်ပါဖော်မြူလာကို အသုံးပြုနိုင်ပါသည်။

• MCC = (TP*TN – FP*FN) / √ (TP+FP)(TP+FN)(TN+FP)(TN+FN)
• MCC = (15*375-5*5) / √ (15+5)(15+5)(375+5)(375+5)
• MCC = 0.7368

Matthews ဆက်စပ်ကိန်းသည် 0.7368 ဖြစ်လာသည်။

ဤတန်ဖိုးသည် တစ်ခုနှင့်တစ်ခုအတန်ငယ်နီးစပ်နေပြီး၊ မော်ဒယ်သည် ကစားသမားများကို ရေးဆွဲမည်လား မလုပ်ဆောင်မည်ကို ကြိုတင်ခန့်မှန်းရန် သင့်လျော်သောအလုပ်တစ်ခု လုပ်ဆောင်နေကြောင်း ညွှန်ပြနေသည်။

အောက်ဖော်ပြပါ ဥပမာသည် R ရှိ mltools ပက်ကေ့ခ်ျမှ mcc() လုပ်ဆောင်ချက်ကို အသုံးပြု၍ ဤသတ်သတ်မှတ်မှတ်အခြေအနေအတွက် MCC တွက်ချက်နည်းကို ပြသထားသည်။

ဥပမာ- R တွင် Matthews Correlation Coefficient ကို တွက်ချက်ခြင်း။

အောက်ပါကုဒ်သည် ခန့်မှန်းထားသော အတန်းများ၏ vector တစ်ခုနှင့် အမှန်တကယ် အတန်းများ၏ vector ကို မည်သို့ သတ်မှတ်ရမည်ကို ပြသပြီး mltools ပက်ကေ့ဂျ်မှ mcc() လုပ်ဆောင်ချက်ကို အသုံးပြု၍ Matthews ဆက်စပ်ကိန်းကို တွက်ချက်ပါ-

 library (mltools)

#define vector of actual classes
actual <- rep (c(1, 0), times =c(20, 380))

#define vector of predicted classes
preds <- rep (c(1, 0, 1, 0), times =c(15, 5, 5, 375))

#calculate Matthews correlation coefficient
mcc(preds, actual)

[1] 0.7368421

Matthews ဆက်စပ်ကိန်းသည် 0.7368 ဖြစ်သည်။

၎င်းသည် အစောပိုင်းက ကျွန်ုပ်တို့ကိုယ်တိုင်တွက်ချက်ထားသော တန်ဖိုးနှင့် ကိုက်ညီပါသည်။

ရှုပ်ထွေးမှုမက်ထရစ်အတွက် Matthews ဆက်စပ်ကိန်းကို တွက်ချက်လိုပါက confusionM အကြောင်းပြချက်ကို အောက်ပါအတိုင်း အသုံးပြုနိုင်ပါသည်။

 library (mltools)

#create confusion matrix
conf_matrix <- matrix(c(15, 5, 5, 375), nrow= 2 )

#view confusion matrix
conf_matrix

     [,1] [,2]
[1,] 15 5
[2,] 5,375

#calculate Matthews correlation coefficient for confusion matrix
mcc(confusionM = conf_matrix)

[1] 0.7368421

တဖန် Matthews ဆက်စပ်ကိန်းသည် 0.7368 ဖြစ်သည်။

ထပ်လောင်းအရင်းအမြစ်များ

အောက်ဖော်ပြပါ သင်ခန်းစာများသည် R တွင် အခြားဘုံအလုပ်များကို မည်သို့လုပ်ဆောင်ရမည်ကို ရှင်းပြသည်-

R တွင် logistic regression ကို မည်သို့လုပ်ဆောင်ရမည်နည်း
ggplot2 ကိုသုံးပြီး ROC မျဉ်းကွေးကို ဘယ်လိုဆွဲမလဲ။
R တွင် F1 ရမှတ်ကိုဘယ်လိုတွက်မလဲ။