R တွင် ols regression ကို မည်သို့လုပ်ဆောင်ရမည်နည်း (ဥပမာဖြင့်)

သာမန်အနည်းဆုံးစတုရန်းများ (OLS) ဆုတ်ယုတ်မှုသည် ကျွန်ုပ်တို့အား ကြိုတင်ခန့်မှန်းကိန်းရှင်တစ်ခု သို့မဟုတ် တစ်ခုထက်ပိုသော ကိန်းရှင်များနှင့် တုံ့ပြန်မှုကိန်းရှင် ကြားရှိ ဆက်နွယ်မှုကို အကောင်းဆုံးဖော်ပြသည့် မျဉ်းတစ်ကြောင်းကို ရှာဖွေနိုင်စေသည့် နည်းလမ်းတစ်ခုဖြစ်သည်။

ဤနည်းလမ်းသည် ကျွန်ုပ်တို့အား အောက်ပါညီမျှခြင်းအား ရှာဖွေနိုင်စေသည်-

ŷ = b ₀ + b ₁ x

ရွှေ-

• ŷ : ခန့်မှန်းတုံ့ပြန်မှုတန်ဖိုး
• b ₀ : ဆုတ်ယုတ်မှုမျဉ်း၏ မူလအစ
• b ₁ : ဆုတ်ယုတ်မှုမျဉ်း၏ လျှောစောက်

ဤညီမျှခြင်းသည် ခန့်မှန်းသူနှင့် တုံ့ပြန်မှုကိန်းရှင်ကြား ဆက်နွယ်မှုကို နားလည်ရန် ကူညီပေးနိုင်ပြီး ကြိုတင်ခန့်မှန်းကိန်းရှင်၏တန်ဖိုးကို ပေးထားသည့် တုံ့ပြန်ကိန်းရှင်၏တန်ဖိုးကို ခန့်မှန်းရန် ၎င်းကို အသုံးပြုနိုင်သည်။

အောက်ဖော်ပြပါ အဆင့်ဆင့် ဥပမာသည် R တွင် OLS ဆုတ်ယုတ်မှုကို မည်သို့လုပ်ဆောင်ရမည်ကို ပြသထားသည်။

အဆင့် 1: ဒေတာကိုဖန်တီးပါ။

ဤဥပမာအတွက်၊ ကျွန်ုပ်တို့သည် ကျောင်းသား 15 ဦးအတွက် အောက်ပါ variable နှစ်ခုပါရှိသော ဒေတာအတွဲတစ်ခုကို ဖန်တီးပါမည်။

• စုစုပေါင်းလေ့လာခဲ့သည့် နာရီအရေအတွက်
• စာမေးပွဲရလဒ်

ကျွန်ုပ်တို့သည် တုံ့ပြန်မှုကိန်းရှင်အဖြစ် နာရီများကို ခန့်မှန်းပေးသည့်ကိန်းရှင်နှင့် စာမေးပွဲရမှတ်ကို အသုံးပြု၍ OLS ဆုတ်ယုတ်မှုကို လုပ်ဆောင်ပါမည်။

အောက်ပါကုဒ်သည် ဤဒေတာအတွဲအတုကို R တွင် မည်သို့ဖန်တီးရမည်ကို ပြသသည်-

 #create dataset
df <- data. frame (hours=c(1, 2, 4, 5, 5, 6, 6, 7, 8, 10, 11, 11, 12, 12, 14),
                 score=c(64, 66, 76, 73, 74, 81, 83, 82, 80, 88, 84, 82, 91, 93, 89))

#view first six rows of dataset
head(df)

  hours score
1 1 64
2 2 66
3 4 76
4 5 73
5 5 74
6 6 81

အဆင့် 2- ဒေတာကို မြင်ယောင်ကြည့်ပါ။

OLS ဆုတ်ယုတ်မှုကို မလုပ်ဆောင်မီ နာရီနှင့် စာမေးပွဲရမှတ်အကြား ဆက်စပ်မှုကို မြင်သာစေရန် အပိုင်းအစတစ်ခုကို ဖန်တီးကြပါစို့။

 library (ggplot2)

#create scatterplot
ggplot(df, aes(x=hours, y=score)) +
  geom_point(size= 2 )

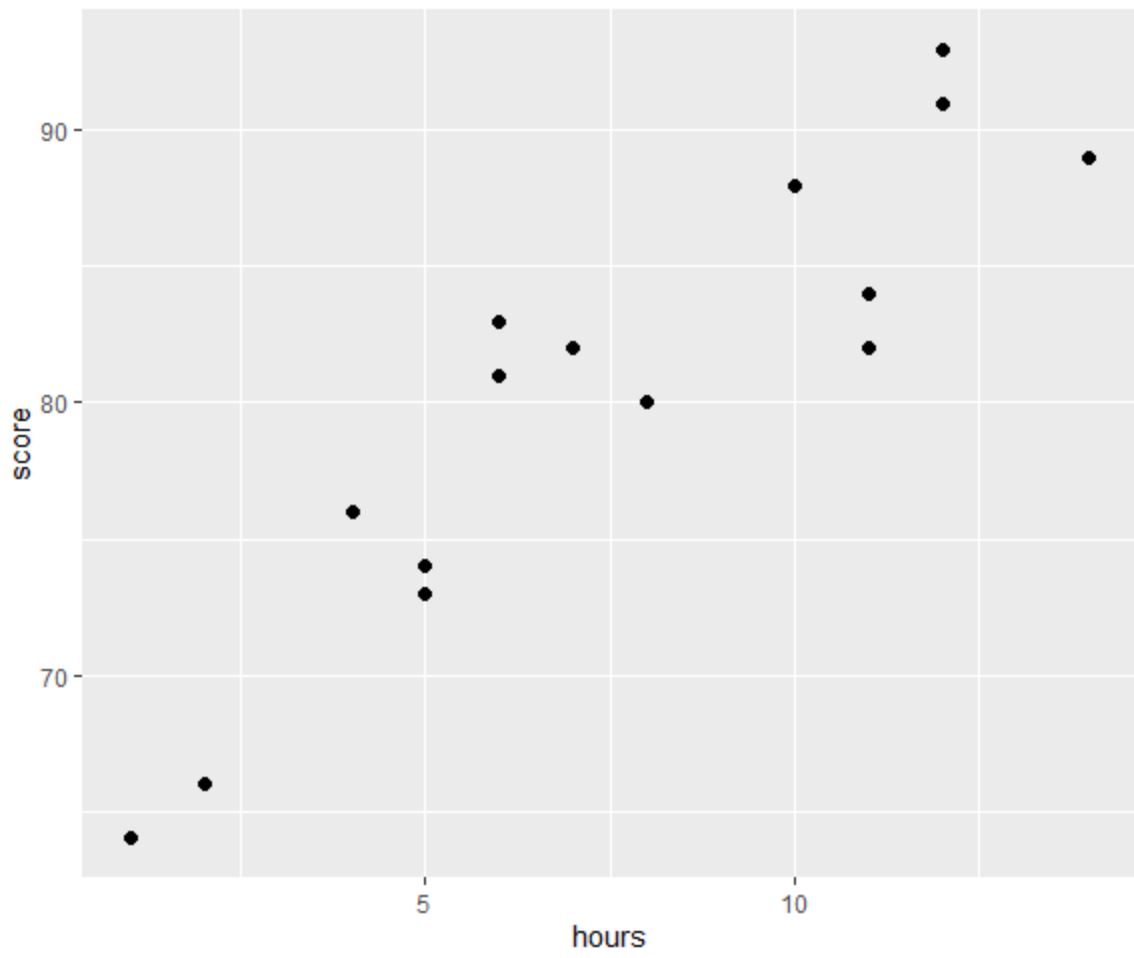
linear regression ၏ ယူဆချက်လေးခု အနက်မှ တစ်ခုသည် ခန့်မှန်းသူနှင့် response variable အကြား linear ဆက်နွယ်မှု ရှိနေသည်။

ဂရပ်မှ ဆက်စပ်မှုကို မျဉ်းသားပုံပေါ်ကြောင်း ကျွန်ုပ်တို့ မြင်နိုင်သည်။ နာရီအရေအတွက်များလာသည်နှင့်အမျှ ရမှတ်သည်လည်း မျဉ်းဖြောင့်အတိုင်း တိုးလာပါသည်။

ထို့နောက် စာမေးပွဲရလဒ်များ ဖြန့်ဝေမှုကို မြင်သာစေရန်နှင့် ကွာဟမှုများကို စစ်ဆေးရန် boxplot တစ်ခုကို ဖန်တီးနိုင်သည်။

မှတ်ချက် – R သည် တတိယ quartile ထက် 1.5 ဆ သို့မဟုတ် ပထမ quartile အောက်ရှိ interquartile အပိုင်းအခြား 1.5 ဆ သို့မဟုတ် ကွာတားအကွာအဝေး၏ 1.5 ဆ ဖြစ်ပါက စောင့်ကြည့်မှုတစ်ခုကို အကြမ်းဖျင်းအဖြစ် သတ်မှတ်သည်။

သတိပြုစရာတစ်ခုက ပိုသာလွန်ပါက၊ ကွက်လပ်တွင် စက်ဝိုင်းငယ်တစ်ခု ပေါ်လာပါမည်-

 library (ggplot2)

#create scatterplot
ggplot(df, aes(y=score)) +
  geom_boxplot() 

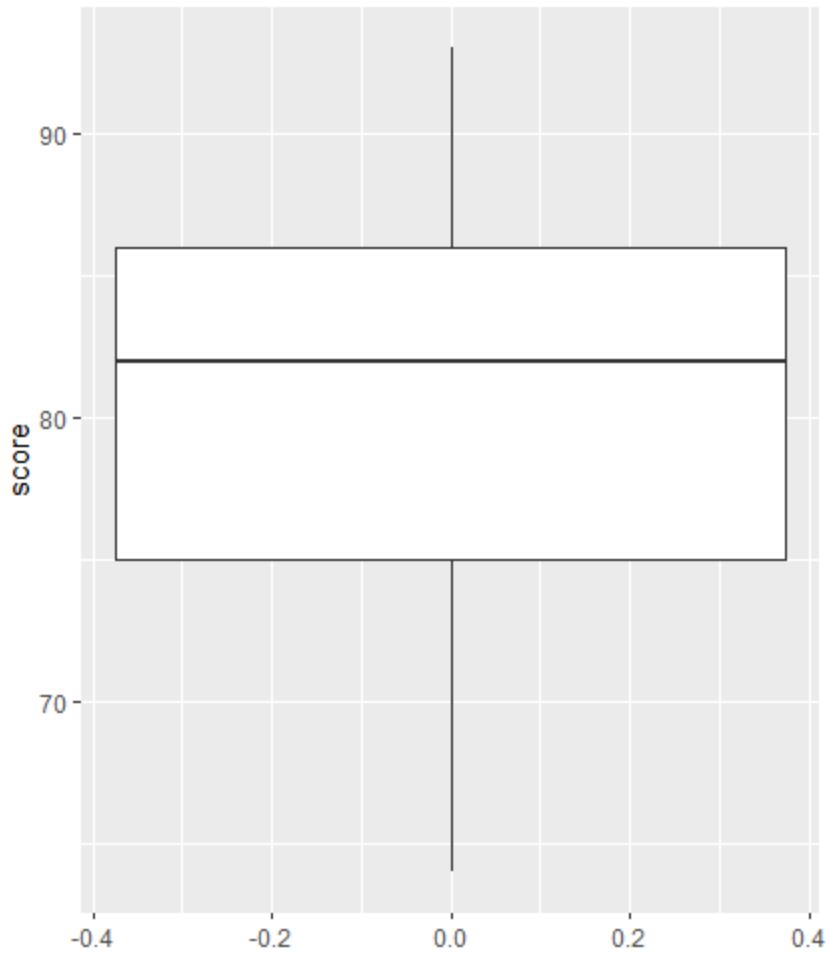
boxplot တွင် စက်ဝိုင်းငယ်များမရှိပါ၊ ဆိုလိုသည်မှာ ကျွန်ုပ်တို့၏ဒေတာအတွဲတွင် အစွန်းထွက်များမရှိပါ။

အဆင့် 3- OLS Regression လုပ်ဆောင်ပါ။

ထို့နောက်၊ ကျွန်ုပ်တို့သည် R တွင် lm() လုပ်ဆောင်ချက်ကို အသုံးပြုပြီး OLS ဆုတ်ယုတ်မှုလုပ်ဆောင်ရန်၊ ကြိုတင်ခန့်မှန်းကိန်းရှင်အဖြစ် နာရီနှင့် တုံ့ပြန်မှုကိန်းရှင်အဖြစ် ရမှတ်တို့ကို အသုံးပြု၍ OLS ဆုတ်ယုတ်မှုလုပ်ဆောင်နိုင်သည်-

 #fit simple linear regression model
model <- lm(score~hours, data=df)

#view model summary
summary(model)

Call:
lm(formula = score ~ hours)

Residuals:
   Min 1Q Median 3Q Max 
-5,140 -3,219 -1,193 2,816 5,772 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 65,334 2,106 31,023 1.41e-13 ***
hours 1.982 0.248 7.995 2.25e-06 ***
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 3.641 on 13 degrees of freedom
Multiple R-squared: 0.831, Adjusted R-squared: 0.818 
F-statistic: 63.91 on 1 and 13 DF, p-value: 2.253e-06

မော်ဒယ်အကျဉ်းချုပ်မှ၊ တပ်ဆင်ထားသော ဆုတ်ယုတ်မှုညီမျှခြင်းမှာ-

ရမှတ် = 65.334 + 1.982*(နာရီ)

ဆိုလိုသည်မှာ ထပ်လောင်းလေ့လာသော နာရီတိုင်းသည် ပျမ်းမျှ စာမေးပွဲရမှတ် 1,982 မှတ် တိုးလာခြင်းနှင့် ဆက်စပ်နေသည်။

65,334 ၏မူရင်းတန်ဖိုးသည် သုညနာရီစာလေ့လာနေသည့် ကျောင်းသားအတွက် ပျမ်းမျှမျှော်မှန်းထားသော စာမေးပွဲရမှတ်ကို ပြောပြသည်။

ကျောင်းသားတစ်ဦး၏လေ့လာမှုနာရီအရေအတွက်အပေါ်အခြေခံ၍မျှော်လင့်ထားသောစာမေးပွဲရမှတ်ကိုရှာဖွေရန်ဤညီမျှခြင်းကိုလည်းအသုံးပြုနိုင်သည်။

ဥပမာအားဖြင့်၊ 10 နာရီကြာလေ့လာသော ကျောင်းသားသည် စာမေးပွဲရမှတ် 85.15 ရရှိသင့်သည် ။

ရမှတ် = 65.334 + 1.982*(10) = 85.15

ကျန်မော်ဒယ်အကျဉ်းချုပ်ကို ဤအရာက မည်သို့အဓိပ္ပာယ်ဖွင့်ဆိုနိုင်သည်-

• Pr(>|t|) : ၎င်းသည် မော်ဒယ်ဖော်ကိန်းများနှင့် ဆက်စပ်နေသည့် p-တန်ဖိုးဖြစ်သည်။ နာရီ များအတွက် p-value (2.25e-06) သည် 0.05 ထက် သိသိသာသာ နည်းနေသောကြောင့်၊ နာရီ နှင့် ရမှတ် ကြားတွင် ကိန်းဂဏန်းအရ သိသာထင်ရှားသော ဆက်စပ်မှုရှိသည်ဟု ကျွန်ုပ်တို့ပြောနိုင်သည်။
• Multiple R-squared- စာမေးပွဲရမှတ်များတွင် ကွဲလွဲမှုရာခိုင်နှုန်းကို လေ့လာသည့်နာရီအရေအတွက်ဖြင့် ရှင်းပြနိုင်သည်ဟု ဤနံပါတ်က ကျွန်ုပ်တို့အား ပြောပြသည်။ ယေဘူယျအားဖြင့်၊ regression model တစ်ခု၏ R-squared တန်ဖိုး ပိုကြီးလေ၊ ခန့်မှန်းသူ variable များသည် တုံ့ပြန်မှု variable ၏ တန်ဖိုးကို ခန့်မှန်းရာတွင် ပိုကောင်းလေဖြစ်သည်။ ဤကိစ္စတွင်၊ ရမှတ်များကွဲလွဲမှု၏ 83.1% ကို နာရီများဖြင့် ရှင်းပြနိုင်သည်။
• ကျန်နေသောစံလွဲချော်မှု- ဤသည်မှာ သတိပြုမိသောတန်ဖိုးများနှင့် ဆုတ်ယုတ်မှုမျဉ်းကြားရှိ ပျမ်းမျှအကွာအဝေးဖြစ်သည်။ ဤတန်ဖိုးနိမ့်လေ၊ ဆုတ်ယုတ်မှုမျဉ်းသည် စောင့်ကြည့်လေ့လာထားသော အချက်အလက်များနှင့် ကိုက်ညီနိုင်လေဖြစ်သည်။ ဤကိစ္စတွင်၊ စာမေးပွဲတွင်တွေ့ရသော ပျမ်းမျှရမှတ်သည် ဆုတ်ယုတ်မှုမျဉ်းမှ ခန့်မှန်းရမှတ်မှ 3,641 မှတ်ဖြင့် သွေဖည်သွားပါသည်။
• F-statistic နှင့် p-value- F-statistic ( 63.91 ) နှင့် သက်ဆိုင်သော p-value ( 2.253e-06 ) သည် ဆုတ်ယုတ်မှုပုံစံ၏ ယေဘုယျအဓိပ္ပာယ်ကို ပြောပြသည်၊ ဆိုလိုသည်မှာ မော်ဒယ်ရှိ ကြိုတင်ခန့်မှန်းကိန်းရှင်များသည် ကွဲလွဲမှုကို ရှင်းပြရန် အသုံးဝင်သလား၊ . တုံ့ပြန်မှု variable တွင်။ ဤဥပမာရှိ p-value သည် 0.05 ထက်နည်းသောကြောင့်၊ ကျွန်ုပ်တို့၏မော်ဒယ်သည် စာရင်းအင်းအရ သိသာထင်ရှား ပြီး ရမှတ် ကွဲလွဲမှုကို ရှင်းပြရာတွင် အသုံးဝင်သည်ဟု ယူဆပါသည်။

အဆင့် 4- ကျန်ရှိသော မြေကွက်များကို ဖန်တီးပါ။

နောက်ဆုံးတွင်၊ ကျွန်ုပ်တို့သည် မျိုးရိုးဗီဇ နှင့် ပုံမှန်ဖြစ်တည်မှု ၏ ယူဆချက်များကို စစ်ဆေးရန် ကျန်နေသောကွက်များကို ဖန်တီးရန် လိုအပ်ပါသည်။

Homoscedasticity ၏ ယူဆချက်မှာ ဆုတ်ယုတ်မှုပုံစံတစ်ခု၏ အကြွင်းအကျန်များသည် ကြိုတင်ခန့်မှန်းကိန်းရှင်တစ်ခု၏ အဆင့်တစ်ခုစီတွင် ခန့်မှန်းခြေအားဖြင့် တူညီသောကွဲလွဲမှုရှိသည်။

ဤယူဆချက်နှင့် ကိုက်ညီကြောင်း စစ်ဆေးရန်၊ ကျန်အကြွင်းများနှင့် ကိုက်ညီမှုရှိသော ကွက်ကွက် တစ်ခုကို ဖန်တီးနိုင်သည်။

x-axis သည် တပ်ဆင်ထားသောတန်ဖိုးများကိုပြသပြီး y-axis သည် အကြွင်းအကျန်များကိုပြသသည်။ အကြွင်းအကျန်များသည် သုညတန်ဖိုးဝန်းကျင်ရှိ ဂရပ်တစ်လျှောက်လုံး ကျပန်းနှင့် တစ်ပြေးညီ ဖြန့်ဝေနေသရွေ့၊ မျိုးတူရိုးကျဖြစ်ခြင်းကို ချိုးဖောက်ခြင်းမဟုတ်ဟု ကျွန်ုပ်တို့ ယူဆနိုင်သည်-

 #define residuals
res <- resid(model)

#produce residual vs. fitted plot
plot(fitted(model), res)

#add a horizontal line at 0 
abline(0,0)

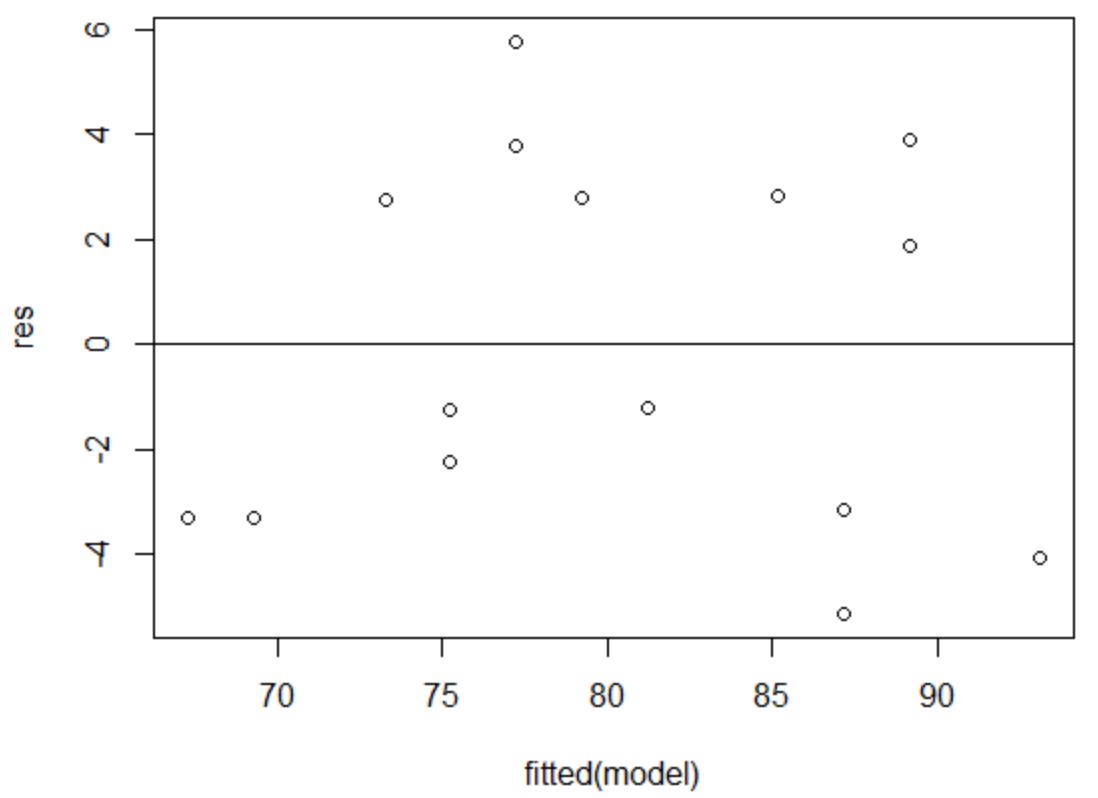
အကြွင်းအကျန်များသည် သုညဝန်းကျင်တွင် ကျပန်းကျပန်း ပြန့်ကျဲနေပုံရပြီး သိသာထင်ရှားသည့်ပုံစံမပြသောကြောင့် ဤယူဆချက်နှင့် ကိုက်ညီပါသည်။

ဆုတ်ယုတ်မှုပုံစံ၏ အကြွင်းအကျန်များသည် ခန့်မှန်းခြေအားဖြင့် ပုံမှန်အတိုင်း ဖြန့်ဝေထားကြောင်း ပုံမှန်ဖြစ်ရိုး ဖြစ်စဉ် ယူဆချက်တွင် ဖော်ပြထားသည်။

ဤယူဆချက်နှင့်ကိုက်ညီမှုရှိမရှိ စစ်ဆေးရန်၊ ကျွန်ုပ်တို့သည် QQ ကွက်ကွက်ကို ဖန်တီးနိုင်သည်။ ကွက်ကွက်အမှတ်များသည် 45 ဒီဂရီထောင့်ကို ဖွဲ့စည်းထားသော အကြမ်းဖျင်းဖြောင့်မျဉ်းကြောင်းတစ်လျှောက်တွင် ရှိနေပါက၊ ဒေတာကို ပုံမှန်အားဖြင့် ဖြန့်ဝေသည်-

 #create QQ plot for residuals
qqnorm(res)

#add a straight diagonal line to the plot
qqline(res) 

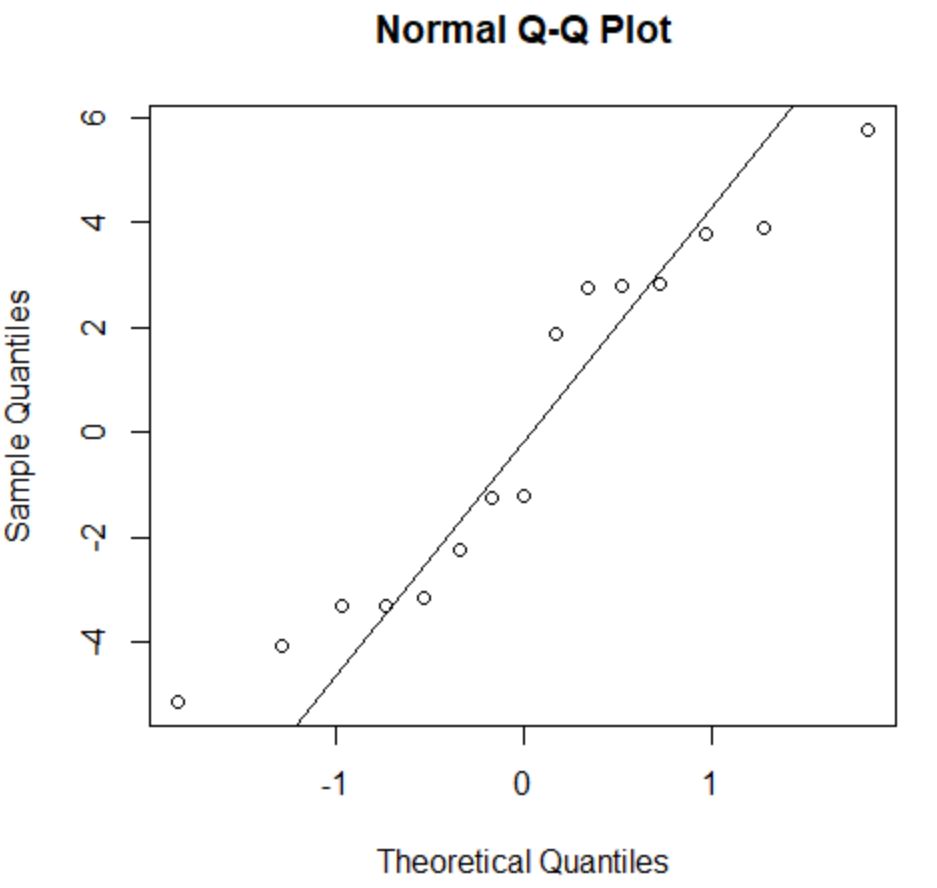
အကြွင်းအကျန်များသည် 45 ဒီဂရီမျဉ်းမှ အနည်းငယ်သွေဖည်သွားသော်လည်း ပြင်းထန်သောစိုးရိမ်မှုဖြစ်စေရန် မလုံလောက်ပါ။ သာမန်ဖြစ်ရိုးဖြစ်စဉ် ယူဆချက်နှင့် ကိုက်ညီသည်ဟု ကျွန်ုပ်တို့ ယူဆနိုင်သည်။

အကြွင်းအကျန်များကို ပုံမှန်အားဖြင့် ဖြန့်ဝေပြီး homoskeastic ဖြစ်သောကြောင့်၊ OLS ဆုတ်ယုတ်မှုပုံစံ၏ ယူဆချက်များနှင့် ကိုက်ညီကြောင်း စစ်ဆေးတွေ့ရှိပါသည်။

ထို့ကြောင့် ကျွန်ုပ်တို့၏ မော်ဒယ်၏ထွက်ရှိမှုသည် ယုံကြည်စိတ်ချရသည်။

မှတ်ချက် – ယူဆချက်တစ်ခု သို့မဟုတ် တစ်ခုထက်ပို၍ မကိုက်ညီပါက၊ ကျွန်ုပ်တို့၏ဒေတာကို ပြောင်းလဲရန် ကြိုးစားနိုင်ပါသည်။

ထပ်လောင်းအရင်းအမြစ်များ

အောက်ဖော်ပြပါ သင်ခန်းစာများသည် R တွင် အခြားဘုံအလုပ်များကို မည်သို့လုပ်ဆောင်ရမည်ကို ရှင်းပြသည်-

R တွင် linear regression အများအပြားလုပ်ဆောင်နည်း
R တွင် exponential regression လုပ်ဆောင်နည်း
R တွင် အလေးချိန် အနည်းဆုံး စတုရန်း ဆုတ်ယုတ်မှုကို မည်သို့လုပ်ဆောင်ရမည်နည်း