R တွင် phi coefficient တွက်ချက်နည်း

Phi coefficient (ရံဖန်ရံခါ ပျမ်းမျှစတုရန်းအခြေအနေဆိုင်ရာကိန်းဂဏန်း ဟု ခေါ်သည်) သည် ဒွိကိန်းရှင်နှစ်ခုကြား ပေါင်းစည်းခြင်း၏ အတိုင်းအတာတစ်ခုဖြစ်သည်။

ကျပန်းပြောင်းလဲနိုင်သော x နှင့် y နှစ်ခုအတွက် ပေးထားသော 2×2 ဇယားတစ်ခုအတွက်

Phi coefficient ကို အောက်ပါအတိုင်း တွက်ချက်နိုင်ပါသည်။

Φ = (AD-BC) / √ (A+B)(C+D)(A+C)(B+D)

ဥပမာ- R တွင် Phi coefficient တွက်ချက်ခြင်း။

နိုင်ငံရေး ပါတီတစ်ခုအတွက် ဦးစားပေးမှုတွင် ကျား၊မ ဆက်စပ်မှု ရှိ၊ မရှိ သိလိုသည်ဆိုပါစို့။ ထို့ကြောင့် ကျွန်ုပ်တို့သည် မဲဆန္ဒရှင် ၂၅ ဦး၏ ရိုးရှင်းသော ကျပန်းနမူနာကို ယူပြီး နိုင်ငံရေးပါတီတစ်ခုအတွက် ၎င်းတို့၏ လိုလားချက်အကြောင်း မေးမြန်းပါသည်။

အောက်ပါဇယားသည် စစ်တမ်း၏ရလဒ်များကို ဖော်ပြသည်။

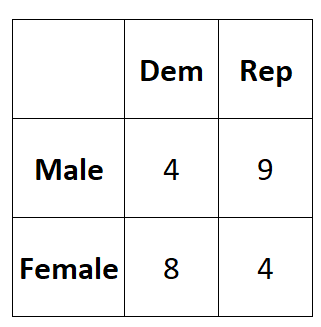
R ရှိ 2×2 matrix တွင် ဤဒေတာကို ထည့်ရန် အောက်ပါကုဒ်ကို အသုံးပြုနိုင်ပါသည်။

 #create 2x2 table
data = matrix(c(4, 8, 9, 4), nrow = 2 )

#view dataset
data

     [,1] [,2]
[1,] 4 9
[2,] 8 4

ထို့နောက် variable နှစ်ခုကြားရှိ Phi coefficient ကိုတွက်ချက်ရန် psych package မှ phi() function ကို အသုံးပြုနိုင်သည်။

 #load psych package
library (psych)

#calculate Phi Coefficient
phi(data)

[1] -0.36

Phi coefficient သည် -0.36 ဖြစ်သွားသည်။

phi လုပ်ဆောင်ချက်သည် ပုံသေအားဖြင့် ဂဏန်း 2 လုံးသို့ လှည့်သည်ကို သတိပြုပါ၊ သို့သော် သင်လိုချင်သလောက် ဂဏန်းများအထိ လှည့်ရန် လုပ်ဆောင်ချက်ကို သင်သတ်မှတ်နိုင်သည်-

 #calculate Phi Coefficient and round to 6 digits
phi(data, digits = 6 )

[1] -0.358974

Phi coefficient ကို ဘယ်လိုအဓိပ္ပာယ်ဖွင့်မလဲ။

Pearson ဆက်စပ်ကိန်းဂဏန်းနှင့်ဆင်တူသည်၊ Phi coefficient သည် -1 နှင့် 1 ကြားရှိတန်ဖိုးများကို ယူသည်-

• -1 သည် ကိန်းရှင်နှစ်ခုကြားတွင် လုံးဝအပျက်သဘောဆောင်သော ဆက်ဆံရေးကို ညွှန်ပြသည်။
• 0 သည် ကိန်းရှင်နှစ်ခုကြားတွင် ဆက်စပ်မှုမရှိကြောင်း ညွှန်ပြသည်။
• 1 သည် ကိန်းရှင်နှစ်ခုကြားတွင် လုံးဝအပြုသဘောဆောင်သော ဆက်ဆံရေးကို ညွှန်ပြသည်။

ယေဘူယျအားဖြင့်၊ နောက်ထပ် Phi coefficient သည် သုညမှဖြစ်ပြီး၊ ကိန်းရှင်နှစ်ခုကြားရှိ ဆက်နွယ်မှု အားကောင်းလေဖြစ်သည်။

တစ်နည်းဆိုရသော် Phi coefficient သည် သုညမှဖြစ်ပြီး၊ variable နှစ်ခုကြားတွင် စနစ်ကျသော ပုံစံအချို့ရှိကြောင်း အထောက်အထား ပိုများလေဖြစ်သည်။

ထပ်လောင်းအရင်းအမြစ်များ

Phi coefficient မိတ်ဆက်
Phi ကိန်းဂဏန်းဂဏန်းတွက်စက်