R တွင် quantile regression ကို မည်သို့လုပ်ဆောင်ရမည်နည်း

Linear regression သည် တစ်ခု သို့မဟုတ် တစ်ခုထက်ပိုသော ကြိုတင်ခန့်မှန်းကိန်းရှင်များနှင့် တုံ့ပြန်မှုကိန်းရှင် အကြား ဆက်နွယ်မှုကို နားလည်ရန် ကျွန်ုပ်တို့ အသုံးပြုနိုင်သည့် နည်းလမ်းတစ်ခုဖြစ်သည်။

ပုံမှန်အားဖြင့်၊ ကျွန်ုပ်တို့သည် linear regression လုပ်ဆောင်သောအခါ၊ တုံ့ပြန်မှုကိန်းရှင်၏ ပျမ်းမျှတန်ဖိုးကို ခန့်မှန်းလိုပါသည်။

သို့သော်၊ ကျွန်ုပ်တို့သည် တုံ့ပြန်မှုတန်ဖိုး၏ ပမာဏ သို့မဟုတ် ရာခိုင်နှုန်းတန်ဖိုး၊ 70th ရာခိုင်နှုန်း၊ 90th ရာခိုင်နှုန်း၊ 98th ရာခိုင်နှုန်းစသည်ဖြင့် ခန့်မှန်းရန် quantile regression ဟုခေါ်သော နည်းလမ်းကို အသုံးပြုနိုင်သည်။

R တွင် quantile regression ကိုလုပ်ဆောင်ရန်၊ အောက်ပါ syntax ကိုအသုံးပြုသည့် quantreg package မှ rq() function ကိုသုံးနိုင်သည်။

 library (quantreg)

model <- rq(y ~ x, data = dataset, tau = 0.5 )

ရွှေ-

• y- တုံ့ပြန်မှု ကိန်းရှင်
• x- ကြိုတင်ခန့်မှန်းနိုင်သော ကိန်းရှင်(များ)
• data- ဒေ တာအတွဲအမည်
• tau- ရှာရန် ရာခိုင်နှုန်း။ မူရင်းသည် ပျမ်းမျှ (tau = 0.5) ဖြစ်သော်လည်း ၎င်းကို 0 နှင့် 1 အကြား မည်သည့်ဂဏန်းအဖြစ် သတ်မှတ်နိုင်သည်။

ဤသင်ခန်းစာသည် R တွင် ပမာဏဆုတ်ယုတ်မှုလုပ်ဆောင်ရန် ဤလုပ်ဆောင်ချက်ကိုအသုံးပြုပုံအဆင့်ဆင့်ကို ဥပမာပေးထားသည်။

အဆင့် 1: ဒေတာကိုထည့်ပါ။

ဤဥပမာအတွက်၊ တက္ကသိုလ်တစ်ခုရှိ မတူညီသောကျောင်းသား 100 အတွက် ရရှိသော နာရီများနှင့် စာမေးပွဲရလဒ်များပါရှိသော ဒေတာအတွဲတစ်ခုကို ကျွန်ုပ်တို့ ဖန်တီးပါမည်။

 #make this example reproducible
set.seed(0)

#create data frame 
hours <- runif(100, 1, 10)
score <- 60 + 2*hours + rnorm(100, mean=0, sd=.45*hours)
df <- data.frame(hours, score)

#view first six rows
head(df)

     hours score
1 9.070275 79.22682
2 3.389578 66.20457
3 4.349115 73.47623
4 6.155680 70.10823
5 9.173870 78.12119
6 2.815137 65.94716

အဆင့် 2- Quantile Regression လုပ်ဆောင်ပါ။

ဆက်လက်၍၊ ကျွန်ုပ်တို့သည် ကြိုတင်ခန့်မှန်းကိန်းရှင်ကိန်းရှင်နှင့် တုံ့ပြန်မှုကိန်းရှင်အဖြစ် စာမေးပွဲရမှတ်များအဖြစ် လေ့လာထားသော နာရီများကို အသုံးပြု၍ အရေအတွက် ဆုတ်ယုတ်မှုပုံစံကို ဖြည့်သွင်းပါမည်။

လေ့လာခဲ့သည့် နာရီအရေအတွက်ပေါ်မူတည်၍ မျှော်မှန်းထားသည့် 90th ရာခိုင်နှုန်း စာမေးပွဲရမှတ်များကို ခန့်မှန်းရန် မော်ဒယ်ကို အသုံးပြုပါမည်။

 library (quantreg)

#fit model
model <- rq(score ~ hours, data = df, tau = 0.9 )

#view summary of model
summary(model)

Call: rq(formula = score ~ hours, tau = 0.9, data = df)

tau: [1] 0.9

Coefficients:
            coefficients lower bd upper bd
(Intercept) 60.25185 59.27193 62.56459
hours 2.43746 1.98094 2.76989

ရလဒ်မှ ခန့်မှန်းခြေ ဆုတ်ယုတ်မှုညီမျှခြင်းကို ကျွန်ုပ်တို့ မြင်နိုင်သည်-

အကြိမ် ၉၀ မြောက် ရာခိုင်နှုန်းစာမေးပွဲရမှတ် = 60.25 + 2.437*(နာရီ)

ဥပမာအားဖြင့်၊ 8 နာရီစာလေ့လာသောကျောင်းသားအားလုံးအတွက် 90th ရာခိုင်နှုန်းရမှတ်သည် 79.75 ဖြစ်သင့်သည်-

၉၀ မြောက် စာမေးပွဲရမှတ် = 60.25 + 2.437*(8) = 79.75 ။

အထွက်သည် ခန့်မှန်းသူကိန်းရှင်၏ ကြားဖြတ်နှင့် အချိန်များအတွက် အပေါ်နှင့်အောက် ယုံကြည်မှုကန့်သတ်ချက်များကိုလည်း ပြသသည်။

အဆင့် 3- ရလဒ်များကို မြင်ယောင်ကြည့်ပါ။

ဂရပ်ပေါ်တွင် တပ်ဆင်ထားသော အရေအတွက် ဆုတ်ယုတ်မှုညီမျှခြင်းနှင့်အတူ ခွဲခြမ်းစိပ်ဖြာမှုတစ်ခုကို ဖန်တီးခြင်းဖြင့် ဆုတ်ယုတ်မှုရလဒ်များကို မြင်ယောင်ကြည့်နိုင်သည်-

 library (ggplot2)

#create scatterplot with quantile regression line
ggplot(df, aes(hours,score)) +
  geom_point() + 
  geom_abline(intercept= coef (model)[1], slope= coef (model)[2]) 

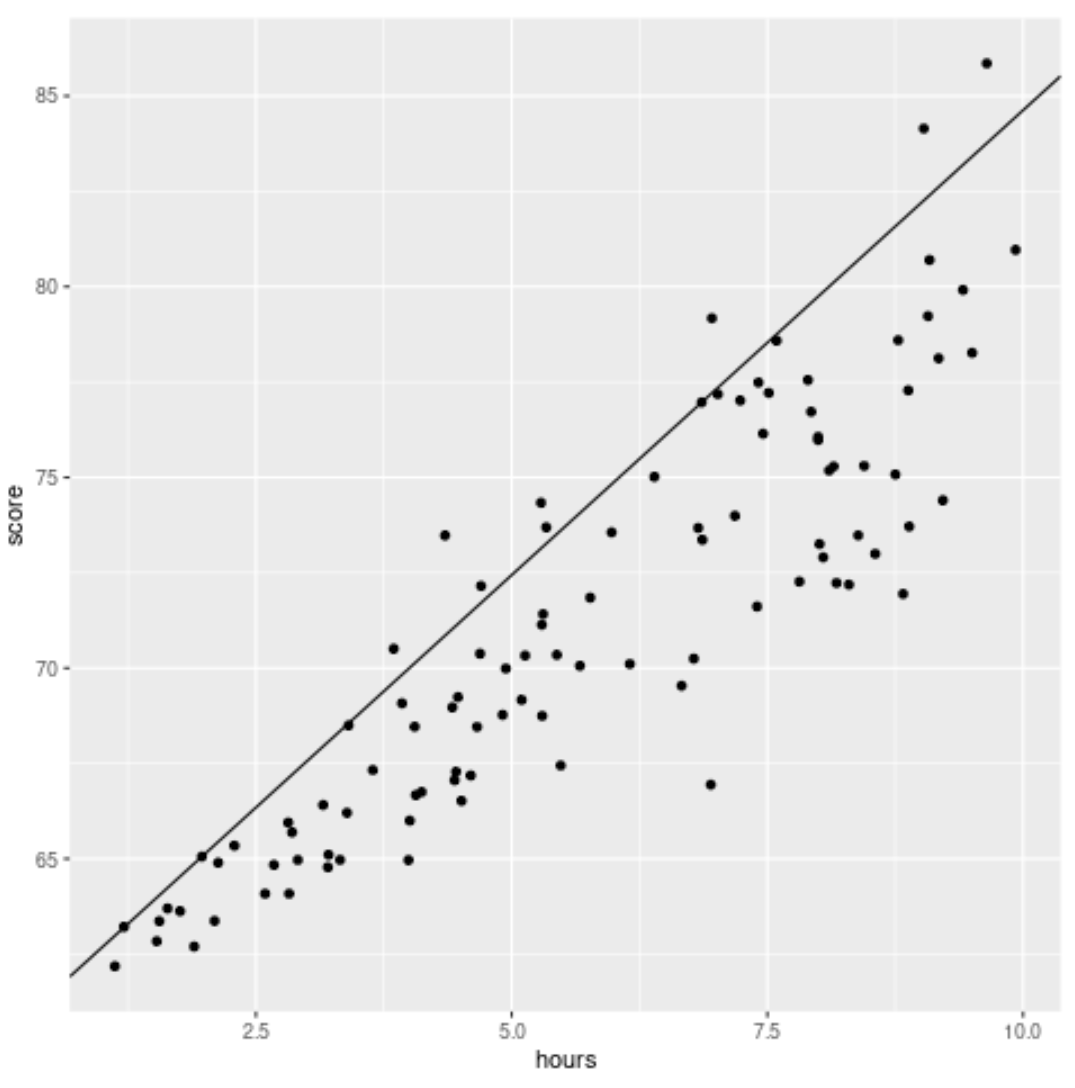
သမားရိုးကျ linear regression line နှင့်မတူဘဲ၊ ဤတပ်ဆင်ထားသောလိုင်းသည် data ၏နှလုံးကိုဖြတ်သွားမည်မဟုတ်ကြောင်းသတိပြုပါ။ ယင်းအစား၊ ၎င်းသည် ခန့်မှန်းသူကိန်းရှင်အဆင့်တစ်ခုစီတွင် ခန့်မှန်းခြေ 90th ရာခိုင်နှုန်းကို ဖြတ်သန်းသွားမည်ဖြစ်သည်။

geom_smooth() အငြင်းအခုံကို ပေါင်းထည့်ခြင်းဖြင့် တပ်ဆင်ထားသော အရေအတွက် ဆုတ်ယုတ်မှုညီမျှခြင်း နှင့် ရိုးရိုးမျဉ်းကြောင်း ဆုတ်ယုတ်မှုညီမျှခြင်းအကြား ခြားနားချက်ကို ကျွန်ုပ်တို့ မြင်နိုင်သည်-

 library (ggplot2)

#create scatterplot with quantile regression line and simple linear regression line
ggplot(df, aes(hours,score)) +
  geom_point() + 
  geom_abline(intercept= coef (model)[1], slope= coef (model)[2]) +
  geom_smooth(method=" lm ", se= F ) 

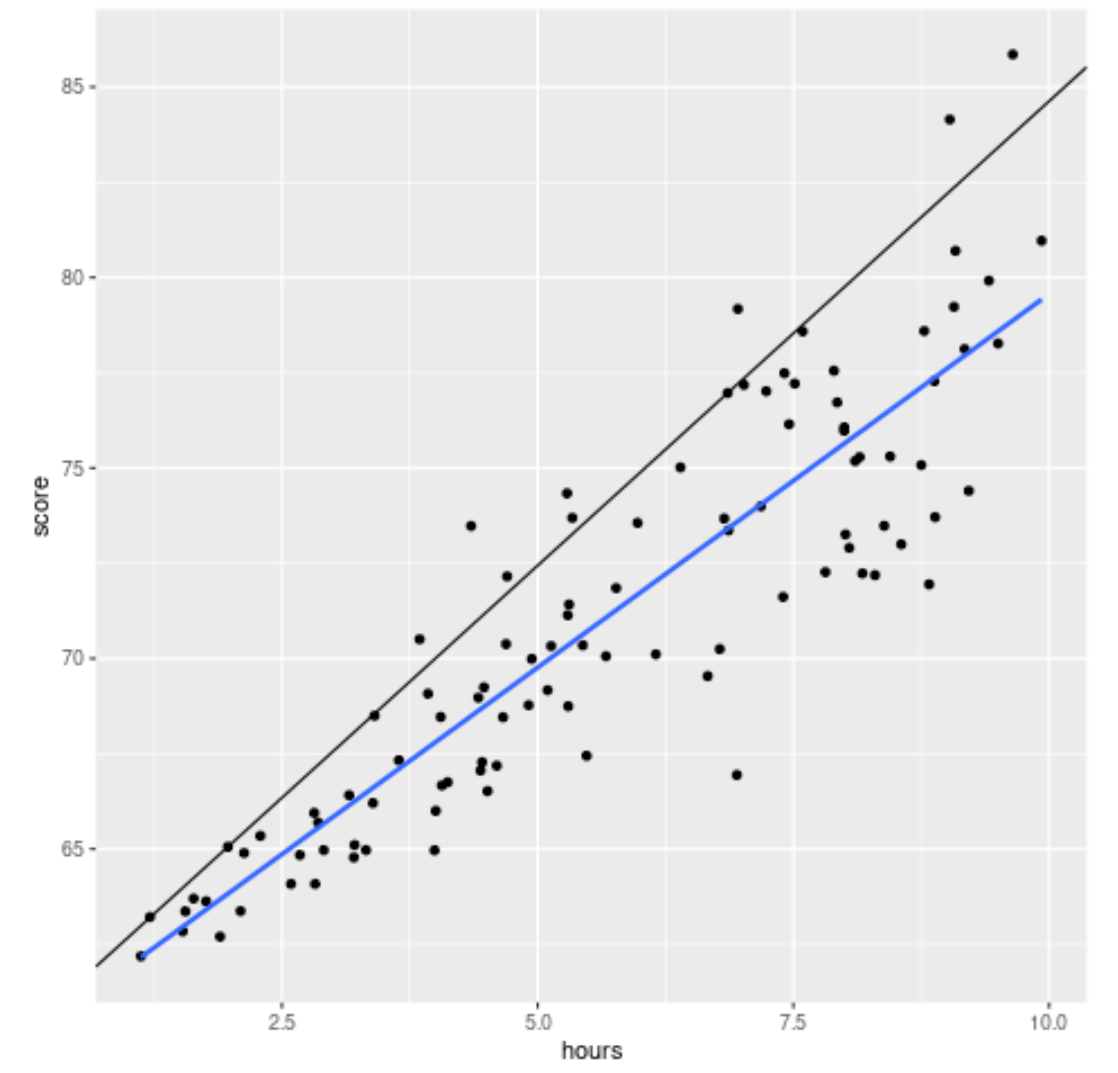
အနက်ရောင်မျဉ်းသည် 90th ရာခိုင်နှုန်းအတွက် ချိန်ညှိထားသော ပမာဏဆုတ်ယုတ်မှုမျဉ်းကို ပြသပြီး အပြာလိုင်းသည် တုံ့ပြန်မှုကိန်းရှင်၏ ပျမ်းမျှတန်ဖိုးကို ခန့်မှန်းပေးသည့် ရိုးရှင်းသောမျဉ်းကြောင်းဆုတ်ယုတ်မှုမျဉ်းကို ပြသသည်။

မျှော်လင့်ထားသည့်အတိုင်း၊ ရိုးရှင်းသောမျဉ်းဖြောင့်ဆုတ်ယုတ်မှုမျဉ်းသည် ဒေတာဖြတ်သန်းပြီး နာရီအဆင့်တစ်ခုစီတွင် စာမေးပွဲရမှတ်များ၏ ခန့်မှန်းပျမ်းမျှတန်ဖိုးကို ပြသည်။

ထပ်လောင်းအရင်းအမြစ်များ

အောက်ဖော်ပြပါ သင်ခန်းစာများသည် R တွင် အခြားဘုံအလုပ်များကို မည်သို့လုပ်ဆောင်ရမည်ကို ရှင်းပြသည်-

R တွင် ရိုးရှင်းသော linear regression လုပ်နည်း
R တွင် linear regression အများအပြားလုပ်ဆောင်နည်း
R တွင် quadratic regression ကို မည်သို့လုပ်ဆောင်ရမည်နည်း။