R တွင် correlation test ကို မည်သို့လုပ်ဆောင်ရမည်နည်း (ဥပမာများဖြင့်)

variable နှစ်ခုကြားရှိ ဆက်နွယ်မှုကို တိုင်းတာရန် နည်းလမ်းတစ်ခုမှာ Pearson correlation coefficient ကို အသုံးပြုခြင်းဖြစ်ပြီး ကိန်းရှင်နှစ်ခုကြားရှိ မျဉ်းကြောင်းဆက်စပ်မှုကို တိုင်းတာခြင်းဖြစ်ပါသည် ။

၎င်းသည် အမြဲတမ်း -1 နှင့် 1 အကြား တန်ဖိုးတစ်ခုကို ယူသည်-

• -1 သည် ကိန်းရှင်နှစ်ခုကြားတွင် လုံးဝအပျက်သဘောဆောင်သော ဆက်စပ်ဆက်နွယ်မှုကို ညွှန်ပြသည်။
• 0 သည် variable နှစ်ခုကြားတွင် linear ဆက်စပ်မှုမရှိဟု ညွှန်ပြသည်။
• 1 သည် ကိန်းရှင်နှစ်ခုကြားတွင် လုံးဝအပြုသဘောဆောင်သောမျဉ်းကြောင်းဆက်စပ်မှုကို ညွှန်ပြသည်။

ဆက်စပ်ကိန်းဂဏန်းတစ်ခုသည် ကိန်းဂဏန်းအရ သိသာထင်ရှားမှုရှိမရှိ ဆုံးဖြတ်ရန်၊ သက်ဆိုင်ရာ t-score နှင့် p-value ကို တွက်ချက်နိုင်သည်။

ဆက်စပ်ပေါင်းကိန်း (r) ၏ t-score ကို တွက်ချက်ရန် ဖော်မြူလာမှာ-

t = r * √ n-2 / √ 1-r ²

p-တန်ဖိုးကို လွတ်လပ်မှု n-2 ဒီဂရီဖြင့် t-ဖြန့်ဝေမှုအတွက် သက်ဆိုင်သော အမြီးနှစ်စင်း p-တန်ဖိုးအဖြစ် တွက်ချက်သည်။

ဥပမာ- R တွင် ဆက်စပ်စစ်ဆေးမှု

variable နှစ်ခုကြားရှိ ဆက်စပ်ကိန်းများကို ကိန်းဂဏန်းအရ သိသာထင်ရှားစွာ ဆုံးဖြတ်ရန်၊ အောက်ပါ syntax ကိုအသုံးပြု၍ R တွင် ဆက်စပ်မှုစမ်းသပ်မှုကို သင်လုပ်ဆောင်နိုင်သည်-

cor.test(x၊ y၊ method=c(“pearson”၊ “kendall”၊ “spearman”))

ရွှေ-

• x၊ y- ဒစ်ဂျစ်တယ်ဒေတာ ကွက်လပ်များ။
• နည်းလမ်း- vector နှစ်ခုကြား ဆက်စပ်မှုကို တွက်ချက်ရန် အသုံးပြုသည့် နည်းလမ်း။ မူရင်းမှာ “Pearson” ဖြစ်သည်။

ဥပမာအားဖြင့် R တွင် အောက်ပါ vector နှစ်ခုရှိသည် ဆိုပါစို့။

 x <- c(2, 3, 3, 5, 6, 9, 14, 15, 19, 21, 22, 23)
y <- c(23, 24, 24, 23, 17, 28, 38, 34, 35, 39, 41, 43)

variable နှစ်ခုကြား ဆက်စပ်မှုစမ်းသပ်မှု မလုပ်ဆောင်မီ၊ ၎င်းတို့၏ ဆက်ဆံရေးကို မြင်သာစေရန် အမြန်ခွဲခြမ်းစိတ်ဖြာမှုတစ်ခုကို ဖန်တီးနိုင်သည်-

 #create scatterplot
plot(x, y, pch= 16 )

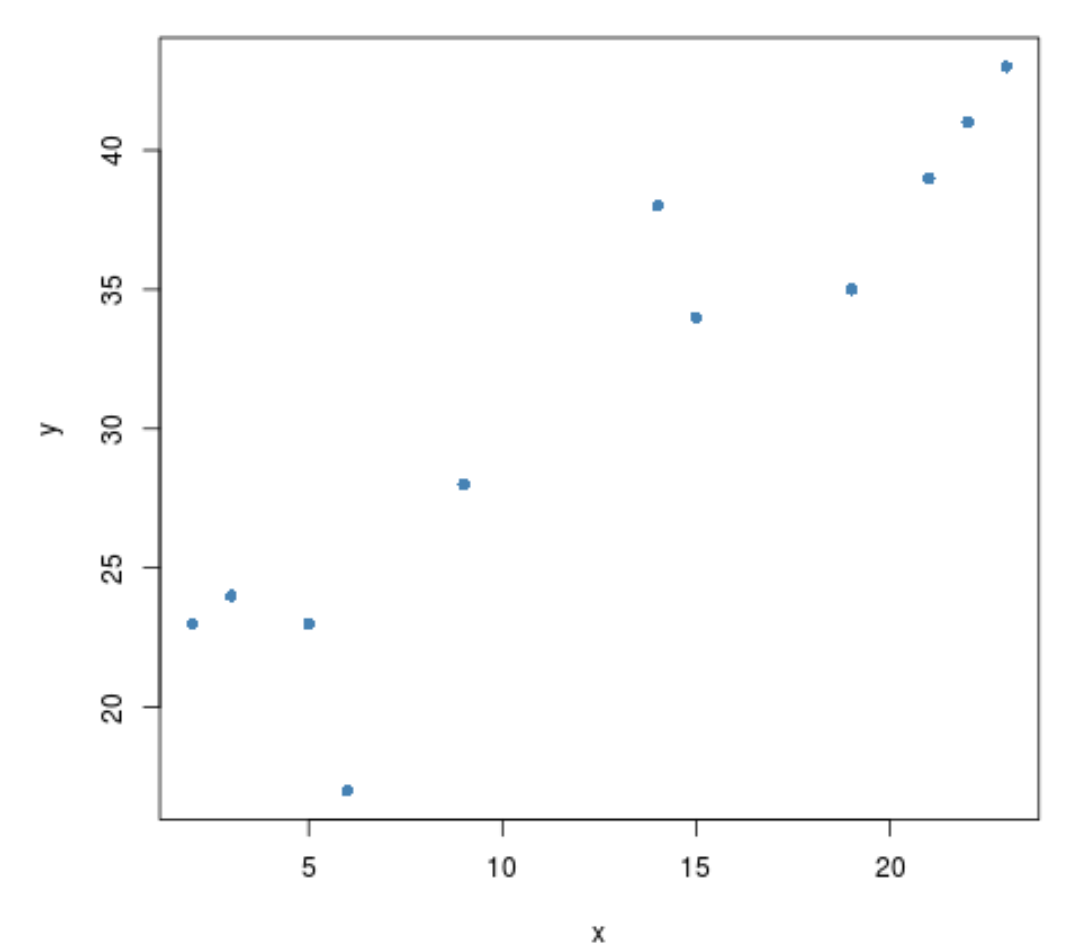
ကိန်းရှင်နှစ်ခုကြားတွင် အပြုသဘောဆောင်သောဆက်စပ်ဆက်နွယ်မှုရှိပုံပေါ်သည်။ ဆိုလိုသည်မှာ တစ်ခုတိုးလာသည်နှင့်အမျှ အခြားတစ်ခုသည်လည်း တိုးလာတတ်သည်။

ဤဆက်စပ်ဆက်နွယ်မှုသည် ကိန်းဂဏန်းအရ သိသာထင်ရှားခြင်းရှိ၊ မရှိ သိရန်၊ ကျွန်ုပ်တို့သည် ဆက်စပ်စမ်းသပ်မှုကို လုပ်ဆောင်နိုင်သည်-

 #perform correlation test between the two vectors
cor.test(x, y)

	Pearson's product-moment correlation

data: x and y
t = 7.8756, df = 10, p-value = 1.35e-05
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
 0.7575203 0.9799783
sample estimates:
      horn 
0.9279869

vector နှစ်ခုကြားရှိ ဆက်စပ်ကိန်းသည် 0.9279869 ဖြစ်သွားသည်။

စမ်းသပ်မှုစာရင်းအင်းသည် 7.8756 နှင့် သက်ဆိုင်သော p-value သည် 1.35e-05 ဖြစ်သည်။

ဤတန်ဖိုးသည် 0.05 ထက်နည်းသောကြောင့်၊ ကိန်းရှင်နှစ်ခုကြားရှိ ဆက်နွယ်မှုသည် စာရင်းအင်းအရ သိသာထင်ရှားသည်ဟု ဆိုရန် လုံလောက်သော အထောက်အထားရှိသည်။

ထပ်လောင်းအရင်းအမြစ်များ

အောက်ဖော်ပြပါ သင်ခန်းစာများတွင် ဆက်စပ်ကိန်းများအကြောင်း နောက်ထပ်အချက်အလက်များကို ပေးဆောင်သည်-

Pearson Correlation Coefficient နိဒါန်း
အဘယ်အရာကို “ ခိုင်မာသော” ဆက်စပ်မှုဟုယူဆသနည်း။
Pearson ၏ဆက်စပ်မှု၏ယူဆချက်ငါးခု