R တွင်နမူနာဖြန့်ဝေမှုများကို တွက်ချက်နည်း

နမူနာဖြန့်ချီခြင်းသည် လူဦးရေတစ်ခုတည်းမှ ကျပန်းနမူနာများစွာကို အခြေခံ၍ အချို့သော ကိန်းဂဏန်း တစ်ခု၏ ဖြစ်နိုင်ခြေဖြန့်ဝေမှုတစ်ခုဖြစ်သည်။

ဤကျူတိုရီရယ်တွင် R တွင်နမူနာဖြန့်ဝေမှုများဖြင့် အောက်ပါအတိုင်းလုပ်ဆောင်နည်းကို ရှင်းပြထားသည်။

• နမူနာဖြန့်ဝေမှုကို ဖန်တီးပါ။
• နမူနာဖြန့်ဝေမှုကို မြင်ယောင်ကြည့်ပါ။
• နမူနာဖြန့်ဖြူးမှု၏ ပျမ်းမျှနှင့် စံသွေဖည်မှုကို တွက်ချက်ပါ။
• နမူနာဖြန့်ဝေမှုနှင့်ပတ်သက်၍ ဖြစ်နိုင်ခြေများကို တွက်ချက်ပါ။

R တွင်နမူနာဖြန့်ဝေမှုတစ်ခုဖန်တီးပါ။

အောက်ပါကုဒ်သည် R တွင်နမူနာဖြန့်ဝေမှုကို မည်သို့ထုတ်လုပ်ရမည်ကို ပြသသည်-

 #make this example reproducible
set.seed(0)

#define number of samples
n = 10000

#create empty vector of length n
sample_means = rep (NA, n)

#fill empty vector with means
for (i in 1:n){
  sample_means[i] = mean ( rnorm (20, mean=5.3, sd=9))
}

#view first six sample means
head(sample_means)

[1] 5.283992 6.304845 4.259583 3.915274 7.756386 4.532656

ဤဥပမာတွင်၊ နမူနာအရွယ်အစားတစ်ခုစီသည် 20 ရှိပြီး ပုံမှန်ဖြန့်ဝေမှုတစ်ခုမှ ပျမ်းမျှနမူနာ 10,000 ကို တွက်ချက်ရန် rnorm() လုပ်ဆောင်ချက်ကို အသုံးပြုထားပါသည်။

ပထမနမူနာတွင် ပျမ်းမျှ 5.283992 ရှိသည်၊ ဒုတိယနမူနာတွင် ပျမ်းမျှ 6.304845 ၊ အစရှိသည်ဖြင့် တွေ့ရှိနိုင်ပါသည်။

နမူနာဖြန့်ဝေမှုကို မြင်ယောင်ကြည့်ပါ။

နမူနာဖြန့်ဝေမှုကို မြင်သာစေရန် ရိုးရှင်းသော ဟီစတိုဂရမ်ကို ဖန်တီးနည်းကို အောက်ပါကုဒ်တွင် ပြသသည်-

 #create histogram to visualize the sampling distribution
hist(sample_means, main = "", xlab = " Sample Means ", col = " steelblue ")

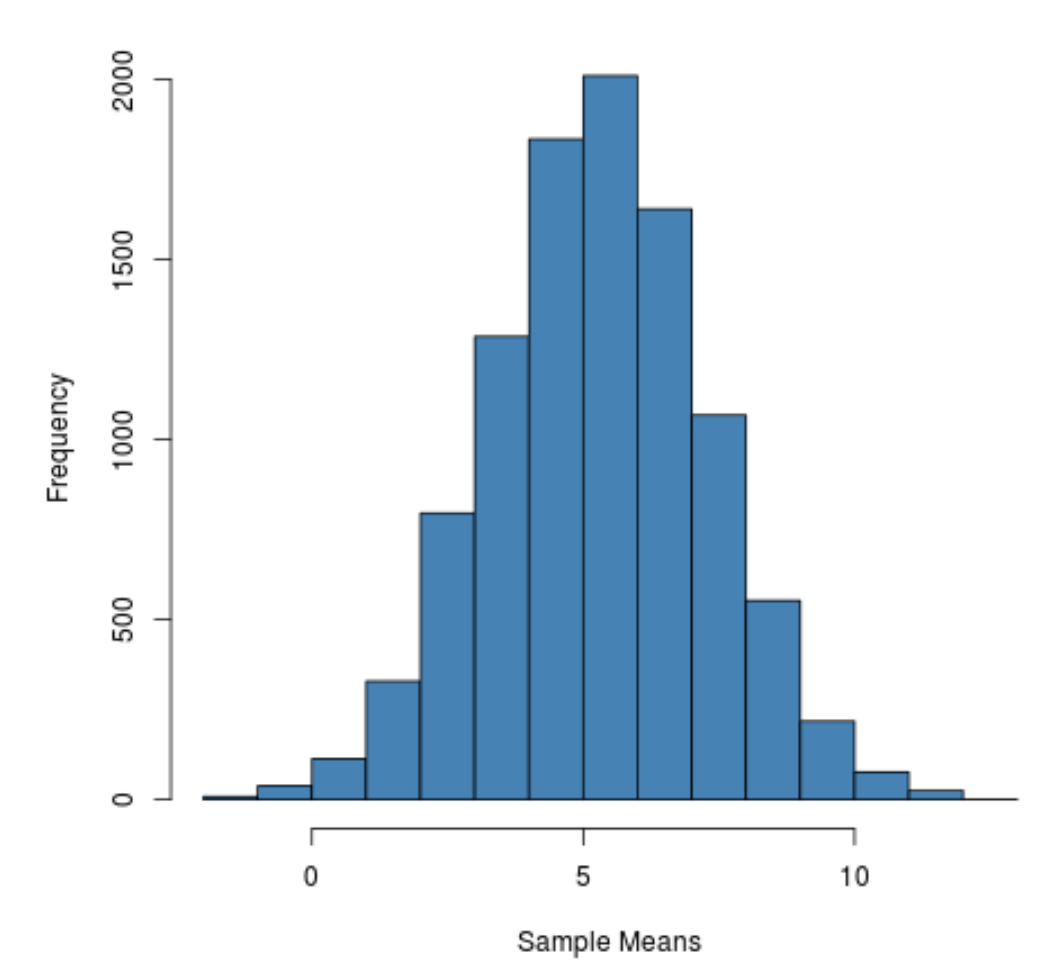
နမူနာဖြန့်ဝေမှုသည် တန်ဖိုး 5 အနီး အထွတ်အထိပ်ရှိ ခေါင်းလောင်းပုံသဏ္ဌာန်ဖြစ်သည်ကို တွေ့မြင်နိုင်သည်။

သို့သော်၊ ဖြန့်ဖြူးမှု၏အမြီးများမှ အချို့နမူနာများသည် 10 ထက်ကြီးသည်ဟု အဓိပ္ပါယ်ရပြီး အချို့မှာ 0 ထက်နည်းသည်ကို ကျွန်ုပ်တို့တွေ့နိုင်သည်။

ပျမ်းမျှနှင့် စံသွေဖည်မှုကို ရှာပါ။

အောက်ပါကုဒ်သည် နမူနာဖြန့်ဝေမှု၏ ပျမ်းမျှနှင့် စံသွေဖည်မှုကို တွက်ချက်နည်းကို ပြသသည်-

 #mean of sampling distribution
mean(sample_means)

[1] 5.287195

#standard deviation of sampling distribution
sd(sample_means)

[1] 2.00224

သီအိုရီအရ၊ နမူနာဖြန့်ဝေမှု၏ပျမ်းမျှသည် 5.3 ဖြစ်သင့်သည်။ ဤဥပမာရှိ အမှန်တကယ်နမူနာဆိုလိုသည်မှာ 5.287195 ဖြစ်ပြီး 5.3 နှင့်နီးစပ်ကြောင်း ကျွန်ုပ်တို့တွေ့မြင်နိုင်ပါသည်။

သီအိုရီအရ၊ နမူနာဖြန့်ချီခြင်း၏ စံသွေဖည်မှုသည် 9 / √20 = 2.012 ဖြစ်မည့် s/√n နှင့် ညီမျှသင့်သည်။ နမူနာဖြန့်ဝေခြင်း၏ အမှန်တကယ်စံသွေဖည်မှုမှာ 2.00224 ဖြစ်ပြီး 2.012 နှင့် နီးစပ်ကြောင်း ကျွန်ုပ်တို့တွေ့မြင်နိုင်ပါသည်။

ဖြစ်နိုင်ခြေများကို တွက်ချက်ပါ။

အောက်ဖော်ပြပါကုဒ်သည် နမူနာဆိုလိုချက်တစ်ခုအတွက် သတ်မှတ်ထားသောတန်ဖိုး၊ လူဦးရေပျမ်းမျှ၊ လူဦးရေစံသွေဖည်မှုနှင့် နမူနာအရွယ်အစားကိုရရှိရန် ဖြစ်နိုင်ခြေကို တွက်ချက်ပုံကို ပြသထားသည်။

 #calculate probability that sample mean is less than or equal to 6
sum(sample_means <= 6) / length(sample_means)

ဤဥပမာတွင်၊ နမူနာဆိုလိုသည် 6 ထက်နည်းသည် သို့မဟုတ် ညီမျှသည်ဖြစ်နိုင်ခြေကို ကျွန်ုပ်တို့ရှာတွေ့သည်၊ လူဦးရေဆိုလိုရင်းမှာ 5.3 ဖြစ်ပြီး လူဦးရေစံသွေဖည်မှုမှာ 9 ဖြစ်ပြီး၊ နမူနာ၏အရွယ်အစားမှာ 0.6417 ဖြစ်သည်။

၎င်းသည် Sampling Distribution Calculator မှတွက်ချက်သော ဖြစ်နိုင်ခြေနှင့် အလွန်နီးစပ်ပါသည်။

ကုဒ်အပြည့်အစုံ

ဤဥပမာတွင်အသုံးပြုသည့် R ကုဒ်အပြည့်အစုံကို အောက်တွင်ဖော်ပြထားသည်-

 #make this example reproducible
set.seed(0)

#define number of samples
n = 10000

#create empty vector of length n
sample_means = rep (NA, n)

#fill empty vector with means
for (i in 1:n){
  sample_means[i] = mean ( rnorm (20, mean=5.3, sd=9))
}

#view first six sample means
head(sample_means)

#create histogram to visualize the sampling distribution
hist(sample_means, main = "", xlab = " Sample Means ", col = " steelblue ")

#mean of sampling distribution
mean(sample_means)

#standard deviation of sampling distribution
sd(sample_means)

#calculate probability that sample mean is less than or equal to 6
sum(sample_means <= 6) / length(sample_means)

ထပ်လောင်းအရင်းအမြစ်များ

နမူနာဖြန့်ဝေမှုများအကြောင်း နိဒါန်း
နမူနာဖြန့်ဝေဂဏန်းတွက်စက်
Central Limit Theorem နိဒါန်း