R (၄) နည်းလမ်းဖြင့် ပုံမှန်အတိုင်း စမ်းသပ်နည်း၊

ကိန်းဂဏန်းစစ်ဆေးမှုများစွာသည် ဒေတာအစုံများကို ပုံမှန်ဖြန့်ဝေသည်ဟု ယူဆသည် ။

R တွင် ဤယူဆချက်ကို စစ်ဆေးရန် ဘုံနည်းလမ်း လေးခုရှိသည်။

1. (အမြင်နည်း) ဟီစတိုဂရမ်တစ်ခု ဖန်တီးပါ။

• ဟီစတိုဂရမ်သည် ခန့်မှန်းခြေအားဖြင့် “ ခေါင်းလောင်း” ပုံသဏ္ဍာန်ဖြစ်ပါက၊ ဒေတာကို ပုံမှန်အတိုင်း ဖြန့်ဝေသည်ဟု ယူဆပါသည်။

2. (Visual Method) QQ ကွက်ကွက်ဖန်တီးပါ။

• ကွက်လပ်ပေါ်ရှိ အမှတ်များသည် ဖြောင့်ထောင့်ဖြတ်မျဉ်းတစ်လျှောက် အကြမ်းဖျင်းအားဖြင့် တည်ရှိနေပါက ဒေတာကို ပုံမှန်အတိုင်း ဖြန့်ဝေသည်ဟု ယူဆပါသည်။

3. (တရားဝင်စာရင်းအင်းစမ်းသပ်မှု) Shapiro-Wilk စမ်းသပ်မှုပြုလုပ်ပါ။

• စမ်းသပ်မှု၏ p-value သည် α = 0.05 ထက် ကြီးပါက ဒေတာကို ပုံမှန်အတိုင်း ဖြန့်ဝေသည်ဟု ယူဆပါသည်။

4. (တရားဝင်စာရင်းအင်းစမ်းသပ်မှု) Kolmogorov-Smirnov စမ်းသပ်မှုပြုလုပ်ပါ။

• စမ်းသပ်မှု၏ p-value သည် α = 0.05 ထက် ကြီးပါက ဒေတာကို ပုံမှန်အတိုင်း ဖြန့်ဝေသည်ဟု ယူဆပါသည်။

အောက်ဖော်ပြပါ ဥပမာများသည် ဤနည်းလမ်းတစ်ခုစီကို လက်တွေ့အသုံးချနည်းကို ပြသထားသည်။

နည်းလမ်း 1- Histogram ဖန်တီးပါ။

အောက်ပါကုဒ်သည် R တွင် ပုံမှန်ဖြန့်ဝေပြီး ပုံမှန်မဟုတ်သော ဖြန့်ဝေထားသောဒေတာအတွဲအတွက် ဟီစတိုဂရမ်ကို ဖန်တီးနည်းကို ပြသသည်-

 #make this example reproducible
set. seeds (0)

#create data that follows a normal distribution
normal_data <- rnorm(200)

#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)

#define plotting region
by(mfrow=c(1,2)) 

#create histogram for both datasets
hist(normal_data, col=' steelblue ', main=' Normal ')
hist(non_normal_data, col=' steelblue ', main=' Non-normal ') 

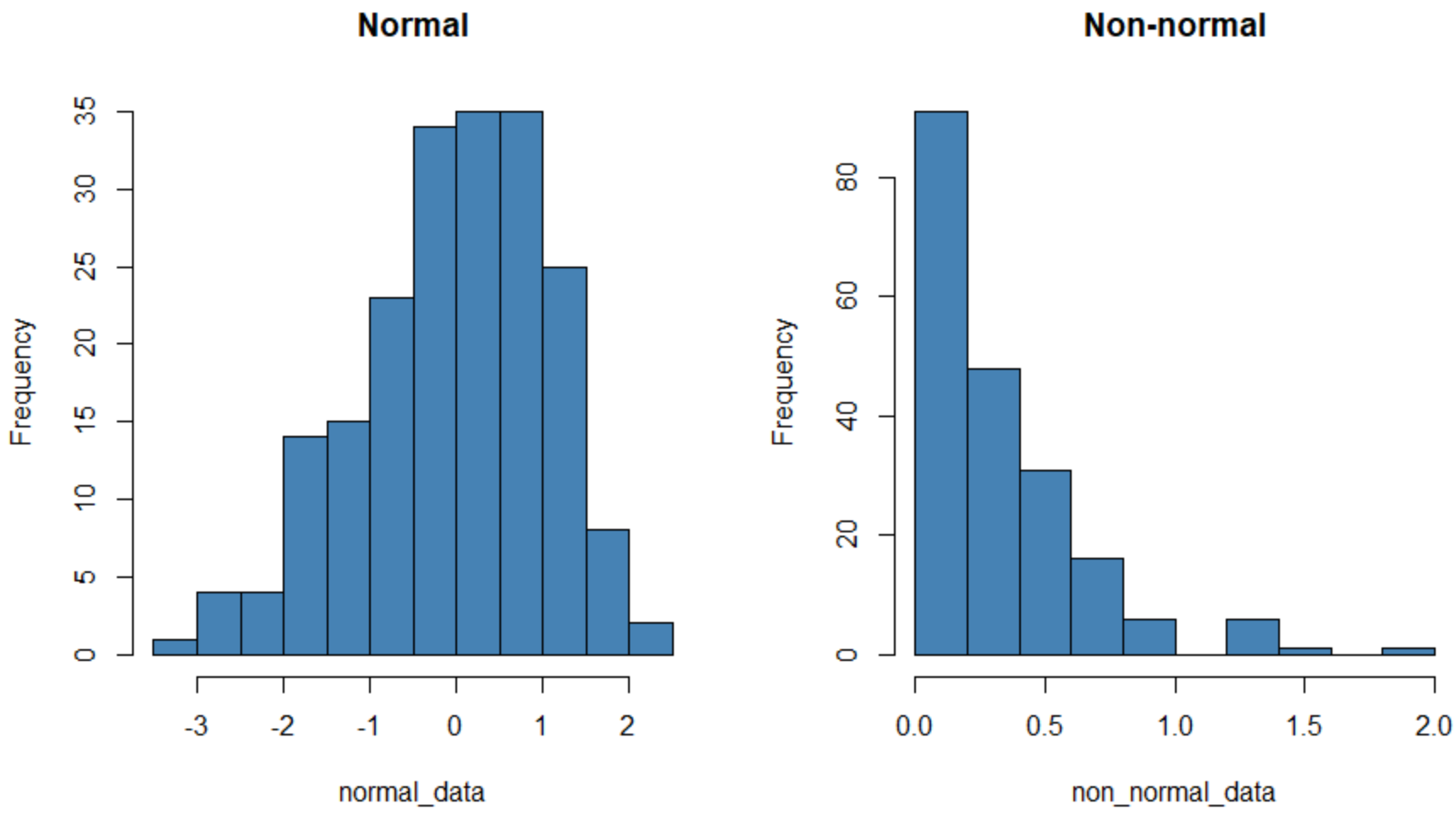
ဘယ်ဘက်ရှိ ဟီစတိုဂရမ်တွင် ပုံမှန်ဖြန့်ဝေထားသည့် ဒေတာအစုတစ်ခု (အကြမ်းဖျင်းအားဖြင့် “ ခေါင်းလောင်းပုံသဏ္ဍာန်) ကို ပြသထားပြီး ညာဘက်တွင်မူ ပုံမှန်ဖြန့်ဝေခြင်းမရှိသည့် ဒေတာအစုတစ်ခုကို ပြသသည်။

နည်းလမ်း 2- QQ Plot တစ်ခုဖန်တီးပါ။

အောက်ပါကုဒ်သည် R တွင် ပုံမှန်ဖြန့်ဝေပြီး ပုံမှန်မဟုတ်သော ဖြန့်ဝေထားသောဒေတာအတွဲအတွက် QQ ကွက်ကွက်ဖန်တီးနည်းကို ပြသသည်-

 #make this example reproducible
set. seeds (0)

#create data that follows a normal distribution
normal_data <- rnorm(200)

#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)

#define plotting region
by(mfrow=c(1,2)) 

#create QQ plot for both datasets
qqnorm(normal_data, main=' Normal ')
qqline(normal_data)

qqnorm(non_normal_data, main=' Non-normal ')
qqline(non_normal_data)

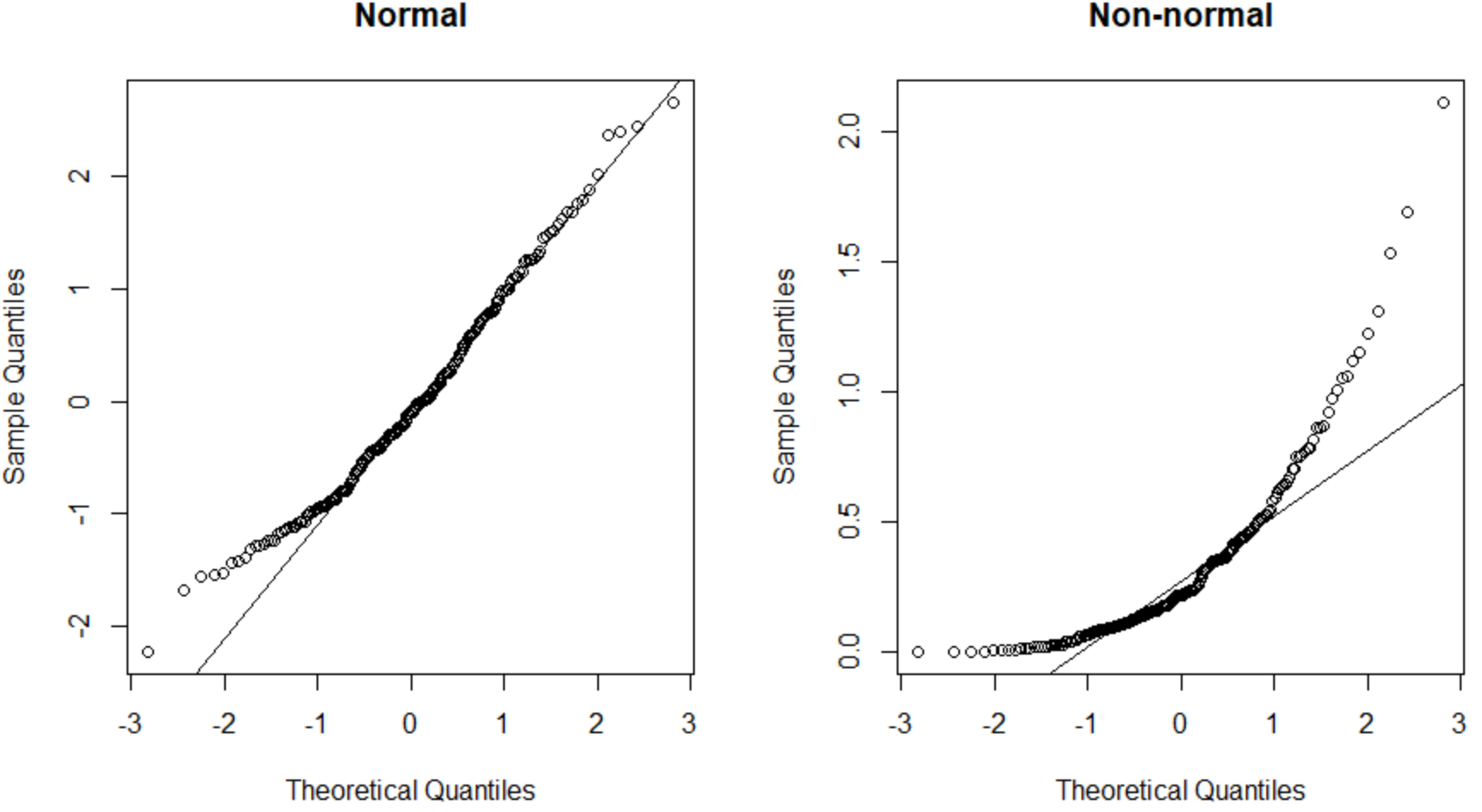
ဘယ်ဘက်ရှိ QQ ကွက်ကွက်သည် ပုံမှန်ဖြန့်ဝေထားသည့် ဒေတာအစုတစ်ခုကို တင်ပြသည် (အချက်များသည် ထောင့်ဖြတ်မျဉ်းဖြောင့်တစ်လျှောက် ကျရောက်သည်) နှင့် ညာဘက်ရှိ QQ ကွက်ကွက်သည် ပုံမှန်ဖြန့်ဝေခြင်းမရှိသည့် ဒေတာအစုတစ်ခုကို တင်ပြသည်။

နည်းလမ်း 3- Shapiro-Wilk စမ်းသပ်မှုပြုလုပ်ပါ။

အောက်ပါကုဒ်သည် R တွင် ပုံမှန်ဖြန့်ဝေပြီး ပုံမှန်မဟုတ်သော ဖြန့်ဝေထားသောဒေတာအတွဲတစ်ခုတွင် Shapiro-Wilk စမ်းသပ်မှုကို မည်သို့လုပ်ဆောင်ရမည်ကို ပြသသည်-

 #make this example reproducible
set. seeds (0)

#create data that follows a normal distribution
normal_data <- rnorm(200)

#perform shapiro-wilk test
shapiro. test (normal_data)

	Shapiro-Wilk normality test

data: normal_data
W = 0.99248, p-value = 0.3952

#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)

#perform shapiro-wilk test
shapiro. test (non_normal_data)

	Shapiro-Wilk normality test

data: non_normal_data
W = 0.84153, p-value = 1.698e-13

ပထမစမ်းသပ်မှု၏ p-တန်ဖိုးသည် 0.05 ထက်မနည်းဘဲ၊ ၎င်းသည် ဒေတာကို ပုံမှန်အတိုင်း ဖြန့်ဝေနေကြောင်း ညွှန်ပြသည်။

ဒုတိယစမ်းသပ်မှု၏ p-တန်ဖိုး သည် 0.05 ထက်နည်းပြီး ဒေတာကို ပုံမှန်ဖြန့်ဝေခြင်းမရှိကြောင်း ညွှန်ပြသည်။

နည်းလမ်း 4- Kolmogorov-Smirnov စမ်းသပ်မှုပြုလုပ်ပါ။

အောက်ပါကုဒ်သည် R တွင် ပုံမှန်ဖြန့်ဝေပြီး ပုံမှန်မဟုတ်သော ဖြန့်ဝေထားသောဒေတာအတွဲတစ်ခုတွင် Kolmogorov-Smirnov စမ်းသပ်မှုကို မည်သို့လုပ်ဆောင်ရမည်ကို ပြသသည်-

 #make this example reproducible
set. seeds (0)

#create data that follows a normal distribution
normal_data <- rnorm(200)

#perform kolmogorov-smirnov test
ks. test (normal_data, ' pnorm ')

	One-sample Kolmogorov–Smirnov test

data: normal_data
D = 0.073535, p-value = 0.2296
alternative hypothesis: two-sided

#create data that follows an exponential distribution
non_normal_data <- rexp(200, rate=3)

#perform kolmogorov-smirnov test
ks. test (non_normal_data, ' pnorm ') 
	One-sample Kolmogorov–Smirnov test

data: non_normal_data
D = 0.50115, p-value < 2.2e-16
alternative hypothesis: two-sided

ပထမစမ်းသပ်မှု၏ p-တန်ဖိုးသည် 0.05 ထက်မနည်းဘဲ၊ ၎င်းသည် ဒေတာကို ပုံမှန်အတိုင်း ဖြန့်ဝေနေကြောင်း ညွှန်ပြသည်။

ဒုတိယစမ်းသပ်မှု၏ p-တန်ဖိုး သည် 0.05 ထက်နည်းပြီး ဒေတာကို ပုံမှန်ဖြန့်ဝေခြင်းမရှိကြောင်း ညွှန်ပြသည်။

ပုံမှန်မဟုတ်သောဒေတာကို ကိုင်တွယ်နည်း

ပေးထားသည့် ဒေတာအစုံကို ပုံမှန်အတိုင်း ဖြန့်ဝေခြင်း မရှိပါက ၊ ၎င်းကို ပုံမှန်အတိုင်း ပိုမိုဖြန့်ဝေနိုင်စေရန် အောက်ပါအသွင်ပြောင်းမှုများထဲမှ တစ်ခုကို ကျွန်ုပ်တို့ မကြာခဏ လုပ်ဆောင်နိုင်သည်-

1. မှတ်တမ်းအသွင်ပြောင်းခြင်း- x တန်ဖိုးများကို log(x) သို့ ပြောင်းလဲပါ။

2. Square root အသွင်ပြောင်းခြင်း- x မှ √x တန်ဖိုးများကို ပြောင်းပါ။

3. Cube root အသွင်ပြောင်းခြင်း- x မှ x ^1/3 တန်ဖိုးများကို ပြောင်းလဲပါ။

ဤအသွင်ပြောင်းမှုများကို လုပ်ဆောင်ခြင်းဖြင့် ဒေတာအတွဲသည် ယေဘူယျအားဖြင့် ပိုမိုပုံမှန်အတိုင်း ဖြန့်ဝေလာပါသည်။

R တွင် ဤအသွင်ပြောင်းမှုများကို မည်သို့လုပ်ဆောင်ရမည်ကို ကြည့်ရှုရန် ဤသင်ခန်းစာကို ဖတ်ပါ။

ထပ်လောင်းအရင်းအမြစ်များ

R တွင် histograms ဖန်တီးနည်း
R တွင် QQ ကွက်ကွက်တစ်ခုကို ဖန်တီးပြီး အဓိပ္ပာယ်ဖွင့်နည်း
R တွင် Shapiro-Wilk စမ်းသပ်မှုပြုလုပ်နည်း
R တွင် Kolmogorov-Smirnov စမ်းသပ်မှုပြုလုပ်နည်း