Rayleigh ဖြန့်ဖြူးမှုမိတ်ဆက်

Rayleigh ဖြန့်ဖြူးမှုသည် သုညနှင့် ညီမျှသော သို့မဟုတ် ပိုကြီးသော တန်ဖိုးများကိုသာ ယူနိုင်သော ကျပန်းကိန်းရှင်များကို စံနမူနာပြုရန်အတွက် အသုံးပြုသည့် စဉ်ဆက်မပြတ်ဖြစ်နိုင်ခြေဖြန့်ဖြူးမှုတစ်ခုဖြစ်သည်။

၎င်းတွင် အောက်ပါဖြစ်နိုင်ခြေ သိပ်သည်းဆ လုပ်ဆောင်မှု ပါရှိသည်။

f(x; σ) = (x/σ ² )e ^{-x 2 /(2σ 2 )}

σ သည် ဖြန့်ဖြူးမှု၏ စကေးကန့်သတ်ချက်ဖြစ်သည်။

Rayleigh ဖြန့်ဖြူးမှု၏ဂုဏ်သတ္တိများ

Rayleigh ဖြန့်ဖြူးမှုတွင် အောက်ပါဂုဏ်သတ္တိများ ရှိသည်။

• ပျမ်းမျှ- σ√ π/2
• သွေဖည်ခြင်း- ((4-π)/2)σ ²
• မုဒ်- σ

π သည် လူသိများသော ကိန်းဂဏာန်းတန်ဖိုးဖြစ်သောကြောင့်၊ ကျွန်ုပ်တို့သည် အောက်ပါအတိုင်း ဂုဏ်သတ္တိများကို ရိုးရှင်းအောင်ပြုလုပ်နိုင်သည်-

• ပျမ်းမျှ: 1.253σ
• သွေဖည်မှု- 0.429σ ²
• မုဒ်- σ

Rayleigh ဖြန့်ဖြူးမှုကို မြင်ယောင်ခြင်း။

စကေးပါရာမီတာအတွက် မတူညီသောတန်ဖိုးများယူသောကြောင့် အောက်ပါဂရပ်သည် Rayleigh ဖြန့်ဖြူးမှု၏ပုံသဏ္ဍာန်ကိုပြသသည်-

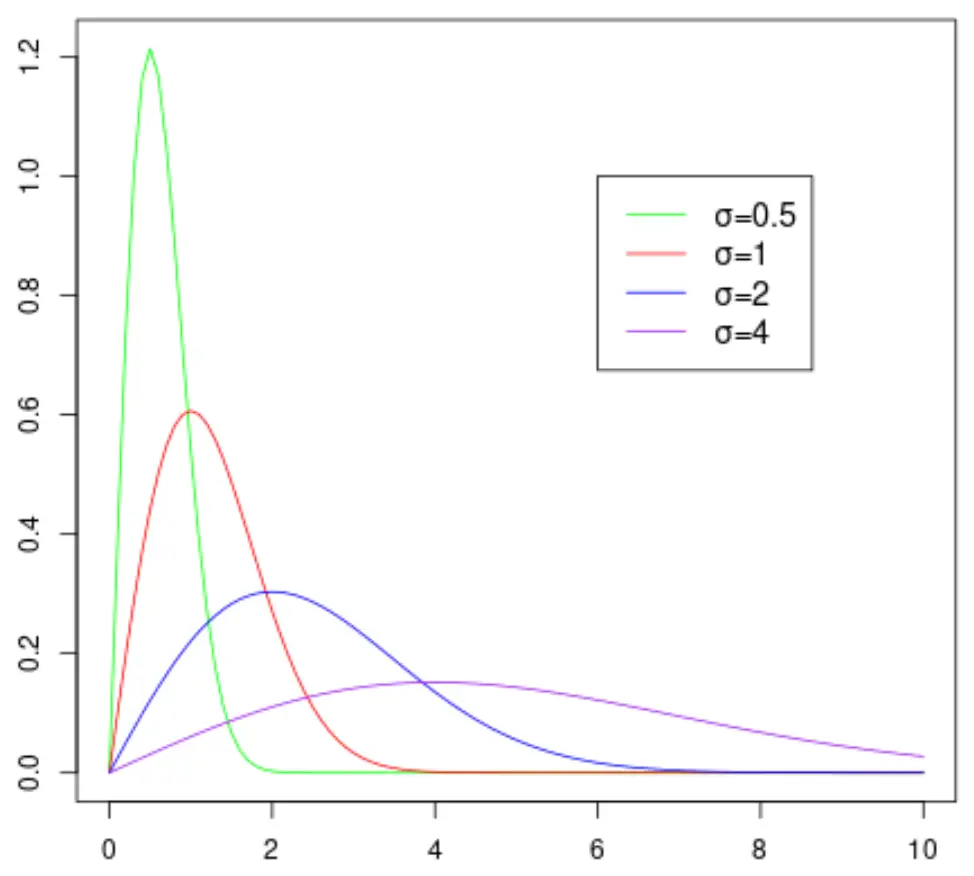
စကေးပါရာမီတာ σ ၏ တန်ဖိုးပိုကြီးလေ၊ ဖြန့်ဖြူးမှု ပိုကျယ်လေ ဖြစ်လာသည်ကို သတိပြုပါ။

အပိုဆု- စူးစမ်းလိုသူများအတွက်၊ အထက်ဖော်ပြပါ ဂရပ်ဖစ်ကို ဖန်တီးရန် အောက်ပါ R ကုဒ်ကို အသုံးပြုခဲ့သည်။

 #load VGAM package
library (VGAM)

#create density plots
curve(drayleigh(x, scale = 0.5), from=0, to=10, col='green')
curve(drayleigh(x, scale = 1), from=0, to=10, col='red', add=TRUE)
curve(drayleigh(x, scale = 2), from=0, to=10, col='blue', add=TRUE)
curve(drayleigh(x, scale = 4), from=0, to=10, col='purple', add=TRUE)

#add legend
legend(6, 1, legend=c("σ=0.5", "σ=1", "σ=2", "σ=4"),
       col=c("green", "red", "blue", "purple"), lty=1, cex=1.2)

အခြားဖြန့်ဝေမှုများနှင့် ဆက်စပ်မှု

Rayleigh ဖြန့်ဖြူးမှုသည် အခြားဖြစ်နိုင်ခြေ ဖြန့်ဝေမှုများနှင့် အောက်ပါ ဆက်စပ်မှု ရှိသည်။

1. စကေးပါရာမီတာ (σ) သည် 1 နှင့် ညီမျှသောအခါ၊ Rayleigh ဖြန့်ဝေမှုသည် လွတ်လပ်မှု 2 ဒီဂရီရှိသော Chi-square ဖြန့်ဖြူးမှုနှင့် ညီမျှသည်။

2. Rayleigh ဖြန့်ဖြူးမှုသည် ပုံသဏ္ဍာန်ဘောင် k = 2 ဖြင့် Weibull ဖြန့်ဖြူးမှု၏ အထူးကိစ္စရပ်ဖြစ်သည်။

3. စကေးပါရာမီတာ σ ပါသော Rayleigh ဖြန့်ဖြူးမှုသည် ဆန်(0, σ) ဖြင့် ဆန်ဖြန့်ဖြူးမှုနှင့် ညီမျှသည်။

လျှောက်လွှာများ

လက်တွေ့တွင်၊ Rayleigh ဖြန့်ဖြူးမှုကို အမျိုးမျိုးသော အပလီကေးရှင်းများတွင် အသုံးပြုသည်-

1. Rayleigh ဖြန့်ဖြူးမှုကို သမုဒ္ဒရာအတွင်းရှိ လှိုင်းများ၏ အမူအကျင့်များကို စံနမူနာပြုရန်၊ လှိုင်းများ၏ အမောက်ရောက်ရန် အချိန်နှင့် လှိုင်းများ၏ အမြင့်ဆုံးအမြင့်သို့ ရောက်ရှိချိန်တို့ အပါအဝင်၊

2. Rayleigh ဖြန့်ဖြူးမှုကို MRI ဟု ပို၍ အများအားဖြင့် သိကြသော သံလိုက်ပဲ့တင်ရိုက်ခတ်မှုပုံရိပ်တွင် နောက်ခံဒေတာများ၏ အမူအကျင့်ကို နမူနာယူရန် အသုံးပြုသည်။

3. Rayleigh ဖြန့်ဖြူးမှုကို အာဟာရနယ်ပယ်တွင် လူနှင့်တိရစ္ဆာန်များတွင် အာဟာရအဆင့်နှင့် အာဟာရတုံ့ပြန်မှုကြား ဆက်နွယ်မှုကို နမူနာယူရန်အတွက် အသုံးပြုသည်။

ထပ်လောင်းအရင်းအမြစ်များ

အောက်ဖော်ပြပါ သင်ခန်းစာများသည် စာရင်းဇယားရှိ အခြားသော ဖြန့်ဖြူးမှုများအကြောင်း နောက်ထပ်အချက်အလက်များကို ပေးဆောင်သည်-

သာမာန်ဖြန့်ဖြူးမှုမိတ်ဆက်
binomial ဖြန့်ဖြူးခြင်းအကြောင်း နိဒါန်း
Poisson ဖြန့်ဖြူးမှုမိတ်ဆက်