Regression slope ၏ အရေးပါပုံကို စမ်းသပ်နည်း

ကျွန်ုပ်တို့တွင် မတူညီသောအိမ် 12 ခု၏ စတုရန်းပုံနှင့် စျေးနှုန်းကိုပြသသည့် အောက်ပါဒေတာအစုံရှိသည် ဆိုကြပါစို့။

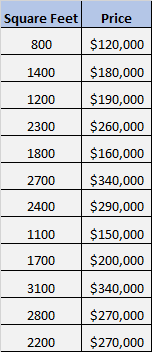
စတုရန်းပေနှင့် ဈေးနှုန်းကြားတွင် သိသာထင်ရှားသော ဆက်စပ်မှုရှိမရှိ သိလိုပါသည်။

ဒေတာပုံသဏ္ဍာန်ကို စိတ်ကူးတစ်ခုရရန်၊ ကျွန်ုပ်တို့သည် ဦးစွာ x-ဝင်ရိုးပေါ်တွင် စတုရန်းပေ နှင့် y-ဝင်ရိုးပေါ်ရှိ စျေးနှုန်းကို ဖန်တီးသည်-

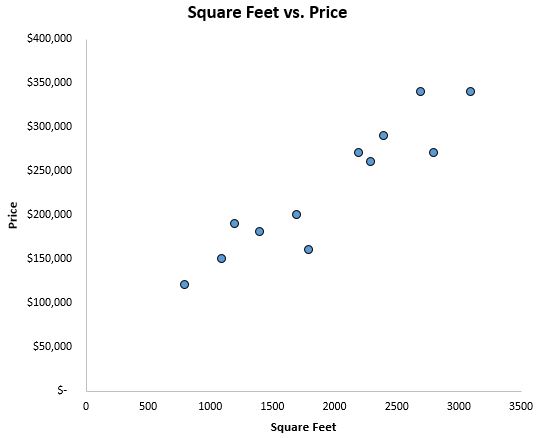
စတုရန်းပုံနှင့် ဈေးနှုန်းကြားတွင် အပြုသဘောဆောင်သော ဆက်စပ်ဆက်နွယ်မှုရှိကြောင်း ကျွန်ုပ်တို့ ရှင်းရှင်းလင်းလင်း သိမြင်နိုင်ပါသည်။ စတုရန်းပုံများ တိုးလာသည်နှင့်အမျှ အိမ်စျေးနှုန်းများလည်း မြင့်တက်လာသည်။

သို့သော်၊ စတုရန်းပုံနှင့် ဈေးနှုန်းကြားတွင် ကိန်းဂဏန်းအချက်အလတ်အရ သိသာထင်ရှားသော ဆက်စပ်မှု ရှိမရှိကို ရှာဖွေရန်၊ ကျွန်ုပ်တို့သည် ရိုးရှင်းသော မျဉ်းသားဆုတ်ယုတ်မှုကို လုပ်ဆောင်ရန် လိုအပ်ပါသည်။

ထို့ကြောင့် ကျွန်ုပ်တို့သည် တုံ့ပြန်မှုအဖြစ် စတုရန်းပေကို ခန့်မှန်းခြင်းနှင့် စျေးနှုန်း အဖြစ် အသုံးပြု၍ ရိုးရှင်းသောမျဉ်းကြောင်းဆုတ်ယုတ်မှု တစ်ခုကို လုပ်ဆောင်ပြီး အောက်ပါရလဒ်ကို ရရှိမည်ဖြစ်သည်။

Excel၊ SPSS၊ R သို့မဟုတ် အခြားဆော့ဖ်ဝဲတစ်ခုခုတွင် ရိုးရှင်းသော မျဉ်းကြောင်းပြန်ဆုတ်ခြင်းကို လုပ်ဆောင်သည်ဖြစ်စေ အထက်ဖော်ပြပါပုံနှင့် ဆင်တူသော ရလဒ်ကို သင်ရရှိမည်ဖြစ်သည်။

ရိုးရှင်းသောမျဉ်းကြောင်းဆုတ်ယုတ်မှုသည် ကျွန်ုပ်တို့၏ခွဲခြမ်းစိတ်ဖြာမှုရှိဒေတာကို အကောင်းဆုံး “ အံဝင်ခွင်ကျသော” မျဉ်း၏ညီမျှခြင်းဖြစ်သည့် အကောင်းဆုံးကိုက်ညီမှုမျဉ်းကို ထုတ်ပေးမည်ကို သတိရပါ။ ဤအသင့်လျော်ဆုံးလိုင်းကို အောက်ပါအတိုင်း သတ်မှတ်သည်။

ŷ = b ₀ + b ₁ x

ŷ သည် တုံ့ပြန်မှုကိန်းရှင်၏ ခန့်မှန်းတန်ဖိုးဖြစ်ပြီး၊ b ₀ သည် ကြားဖြတ်ဖြစ်ပြီး b ₁ သည် ဆုတ်ယုတ်ကိန်းနှင့် x သည် ခန့်မှန်းသူကိန်းရှင်၏တန်ဖိုးဖြစ်သည်။

b ₀ ၏တန်ဖိုးကို 47588.70 ဖြစ်သည့် မူရင်းကိန်းဂဏန်းဖြင့် ပေးပါသည်။

b ₁ ၏တန်ဖိုးကို 93.57 ဖြစ်သည့် ခန့်မှန်းတွက်ချက်နိုင်သော ပြောင်းလဲနိုင်သော Square Feet ၏ coefficient ဖြင့်ပေးသည်။

ထို့ကြောင့် ဤဥပမာတွင် အသင့်တော်ဆုံးမျဉ်းသည် ŷ = 47588.70+ 93.57x ဖြစ်သည်။

ဤသည်မှာ အသင့်တော်ဆုံး စည်းမျဥ်းကို အဓိပ္ပာယ်ဖွင့်ဆိုပုံဖြစ်သည် ။

• b ₀ : စတုရန်းပေ၏တန်ဖိုးသည် သုညဖြစ်သောအခါ၊ မျှော်လင့်ထားသောပျမ်းမျှစျေးနှုန်းတန်ဖိုးမှာ $47,588.70 ဖြစ်သည်။ (ဤကိစ္စတွင် အိမ်တစ်အိမ်သည် သုညစတုရန်းပေ ဘယ်သောအခါမှ မရနိုင်သောကြောင့် ကြားဖြတ်ကို အဓိပ္ပာယ်ဖွင့်ဆိုရန် အဓိပ္ပါယ်မရှိပါ)
• b ₁ : ထပ်လောင်းစတုရန်းပေတစ်ခုစီအတွက်၊ ပျမ်းမျှမျှော်မှန်းထားသည့်စျေးနှုန်းမှာ $93.57 ဖြစ်သည်။

ထို့ကြောင့်၊ နောက်ထပ်စတုရန်းပေတစ်ခုစီအတွက် ပျမ်းမျှမျှော်မှန်းထားသည့်စျေးနှုန်းသည် ၉၃.၅၇ ဒေါ်လာဖြစ်ကြောင်း ယခုကျွန်ုပ်တို့သိပါသည်။

ဤတိုးလာမှုသည် ကိန်းဂဏန်းအရ သိသာထင်ရှားခြင်း ရှိ၊ မရှိ သိရှိရန် B ₁ အတွက် သီအိုရီ စမ်းသပ်မှု ပြုလုပ်ရန် လိုအပ်သည် သို့မဟုတ် B ₁ အတွက် ယုံကြည်မှု ကြားကာလကို တည်ဆောက်ရန် လိုအပ်ပါသည်။

မှတ်ချက် – သီအိုရီစမ်းသပ်မှုနှင့် ယုံကြည်မှုကြားကာလသည် အမြဲတမ်းတူညီသောရလဒ်များကိုပေးလိမ့်မည်။

ဆုတ်ယုတ်လျှောစောက်အတွက် ယုံကြည်မှုကြားကာလတစ်ခု တည်ဆောက်ခြင်း။

ဆုတ်ယုတ်မှုလျှောစောက်အတွက် ယုံကြည်မှုကြားကာလတစ်ခုကို တည်ဆောက်ရန်အတွက်၊ ကျွန်ုပ်တို့သည် အောက်ပါဖော်မြူလာကို အသုံးပြုသည်-

ယုံကြည်မှုကြားကာလ = b ₁ +/- (t _{1-∝/2၊ n-2} ) * (ခ ₁ ၏ စံလွဲချော်မှု)

ရွှေ-

• b ₁ သည် ဆုတ်ယုတ်မှုရလဒ်တွင်ပေးသော slope coefficient ဖြစ်သည်။
• (t _{1-∝/2၊ n-2} ) သည် 1-∝ လွတ်လပ်မှု၏ n-2 ဒီဂရီနှင့် 1-∝ ယုံကြည်မှုအဆင့်အတွက် အရေးပါသော t တန်ဖိုးဖြစ်ပြီး n သည် ကျွန်ုပ်တို့၏ဒေတာအတွဲတွင် လေ့လာတွေ့ရှိချက်စုစုပေါင်းဖြစ်သည်။
• (b ₁ ၏ standard error ) သည် regression result တွင်ပေးထားသော b ₁ ၏စံအမှားဖြစ်သည်

ကျွန်ုပ်တို့၏ဥပမာအားဖြင့်၊ ဤတွင် B ₁ အတွက် 95% ယုံကြည်မှုကြားကာလကို မည်သို့တည်ဆောက်ရမည်နည်း။

• b ₁ သည် regression output မှ 93.57 ဖြစ်သည်။
• ကျွန်ုပ်တို့သည် 95% ယုံကြည်မှုကြားကာလကို အသုံးပြုနေသောကြောင့် ∝ = 0.05 နှင့် n-2 = 12-2 = 10 ဖြစ်သောကြောင့် t _{0.975၊ 10} သည် 2.228 ဖြစ်သည်
• ( _b1 ၏ standard error ) သည် regression output မှ 11.45 ဖြစ်သည်။

ထို့ကြောင့် B ₁ အတွက် ကျွန်ုပ်တို့၏ 95% ယုံကြည်မှုကြားကာလမှာ-

93.57 +/- (2.228) * (11.45) = (68.06၊ 119.08)၊

ဆိုလိုသည်မှာ ထပ်တိုးစတုရန်းပေတစ်ခုစီအတွက် စစ်မှန်သောပျမ်းမျှစျေးနှုန်းတိုးမှုသည် $68.06 နှင့် $119.08 ကြားဖြစ်သည်ကို ကျွန်ုပ်တို့ 95% ယုံကြည်သည်ဟု ဆိုလိုပါသည်။

$0 သည် ဤကြားကာလတွင်မဟုတ်ကြောင်း သတိပြုပါ၊ ထို့ကြောင့် စတုရန်းပုံနှင့်စျေးနှုန်းကြားဆက်ဆံရေးသည် 95% ယုံကြည်မှုအဆင့်တွင် ကိန်းဂဏန်းအရ သိသာထင်ရှားပါသည်။

ဆုတ်ယုတ်မှု လျှောစောက်အတွက် ယူဆချက် စမ်းသပ်မှု ပြုလုပ်ခြင်း။

regression slope အတွက် hypothesis test ပြုလုပ်ရန်၊ hypothesis test အတွက် စံအဆင့်ငါးဆင့်ကို လိုက်နာဆောင်ရွက်ပါ :

အဆင့် ၁။ ယူဆချက်များကို ဖော်ပြပါ။

null hypothesis (H0): B ₁ = 0

အစားထိုးယူဆချက်- (Ha): B ₁ ≠ 0

အဆင့် 2. အသုံးပြုရန် အရေးကြီးသော အဆင့်ကို သတ်မှတ်ပါ။

ယခင်နမူနာတွင် ယုံကြည်မှု 95% ကြားကာလကို တည်ဆောက်ထားသောကြောင့်၊ ဤနေရာတွင် ညီမျှသောချဉ်းကပ်နည်းကို အသုံးပြုပြီး အရေးပါသည့်အဆင့် 0.05 ကို အသုံးပြုရန် ရွေးချယ်ပါမည်။

အဆင့် 3. စမ်းသပ်စာရင်းအင်းနှင့် သက်ဆိုင်ရာ p-value ကိုရှာပါ။

ဤကိစ္စတွင်၊ စမ်းသပ်စာရင်းအင်းသည် t = b ₁ ၏ ဖော်ကိန်း / လွတ်လပ်မှု b ₁ ၏ စံလွဲချော်မှု n-2 ဒီဂရီဖြစ်သည်။ ဆုတ်ယုတ်မှုရလဒ်မှ ဤတန်ဖိုးများကို ကျွန်ုပ်တို့ ရှာဖွေနိုင်သည်-

ထို့ကြောင့် စမ်းသပ်စာရင်းအင်း t = 92.89 / 13.88 = 6.69 ။

လွတ်လပ်မှု 10 ဒီဂရီနှင့် အမြီးနှစ်ပိုင်းစမ်းသပ်မှုဖြင့် ရမှတ် 6.69 ရှိသော T ရမှတ်မှ P တန်ဖိုးဂဏန်းတွက်စက်ကို အသုံးပြု၍ p တန်ဖိုး = 0.000 ဖြစ်သည်။

အဆင့် 4. ပယ်ချခြင်း သို့မဟုတ် မငြင်းဆိုပါနှင့်။

p-value သည် ကျွန်ုပ်တို့၏ အရေးပါမှုအဆင့် 0.05 အောက်ဖြစ်သောကြောင့်၊ ကျွန်ုပ်တို့သည် null hypothesis ကို ငြင်းပယ်ပါသည်။

အဆင့် 5. ရလဒ်များကို ဘာသာပြန်ပါ။

အချည်းနှီးသော အယူအဆကို ကျွန်ုပ်တို့ ပယ်ချလိုက်သောကြောင့်၊ ထပ်တိုးစတုရန်းပေတစ်ခုစီအတွက် စစ်မှန်သော ပျမ်းမျှစျေးနှုန်း မြင့်တက်မှုသည် သုညမဟုတ်ကြောင်း ပြောရန် လုံလောက်သော အထောက်အထားရှိသည်။