Regression slope ၏ standard error ကို နားလည်ခြင်း။

ဆုတ်ယုတ်မှု လျှောစောက်၏ စံအမှား သည် ဆုတ်ယုတ်မှု လျှောစောက်ကို ခန့်မှန်းရာတွင် “ မသေချာမှု” ကို တိုင်းတာသည့် နည်းလမ်းတစ်ခု ဖြစ်သည်။

အောက်ပါအတိုင်း တွက်ချက်သည်။

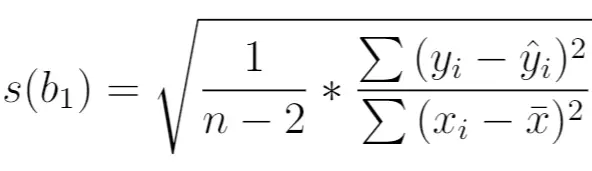
ရွှေ-

• n : စုစုပေါင်းနမူနာအရွယ်အစား
• y _i : တုံ့ပြန်မှုကိန်းရှင်၏ အစစ်အမှန်တန်ဖိုး
• ŷ _i : တုံ့ပြန်မှုကိန်းရှင်၏ ခန့်မှန်းတန်ဖိုး
• x _i : ကြိုတင်ခန့်မှန်းကိန်းရှင်၏ အစစ်အမှန်တန်ဖိုး
• x̄ : ကြိုတင်ခန့်မှန်းကိန်းရှင်၏ ပျမ်းမျှတန်ဖိုး

စံလွဲချော်မှု သေးငယ်လေ၊ ဆုတ်ယုတ်မှု လျှောစောက်အတွက် ကိန်းဂဏန်း ခန့်မှန်းချက် ပတ်လည် ကွဲလွဲမှု နည်းပါးလေဖြစ်သည်။

စာရင်းအင်းဆော့ဖ်ဝဲအများစု၏ ဆုတ်ယုတ်မှုအထွက်တွင် “ စံအမှား” ကော်လံတွင် ဆုတ်ယုတ်မှု၏ စံအမှားကို ပြသပါမည်-

အောက်ဖော်ပြပါနမူနာများသည် မတူညီသောအခြေအနေနှစ်ခုတွင် ဆုတ်ယုတ်မှုလျှောစောက်၏ စံအမှားကို အဓိပ္ပာယ်ဖွင့်ဆိုပုံကို ပြသထားသည်။

ဥပမာ 1- Regression Slope ၏ သေးငယ်သော Standard Error ကို ဘာသာပြန်ခြင်း။

ပါမောက္ခတစ်ဦးသည် စာသင်ချိန်နာရီအရေအတွက်နှင့် ၎င်း၏အတန်းရှိ ကျောင်းသားများ၏ နောက်ဆုံးစာမေးပွဲအဆင့်ကြား ဆက်နွယ်မှုကို နားလည်လိုသည်ဆိုပါစို့။

၎င်းသည် ကျောင်းသား 25 ဦးအတွက် အချက်အလက်များကို စုဆောင်းပြီး အောက်ပါ အပိုင်းအစကို ဖန်တီးပေးသည်-

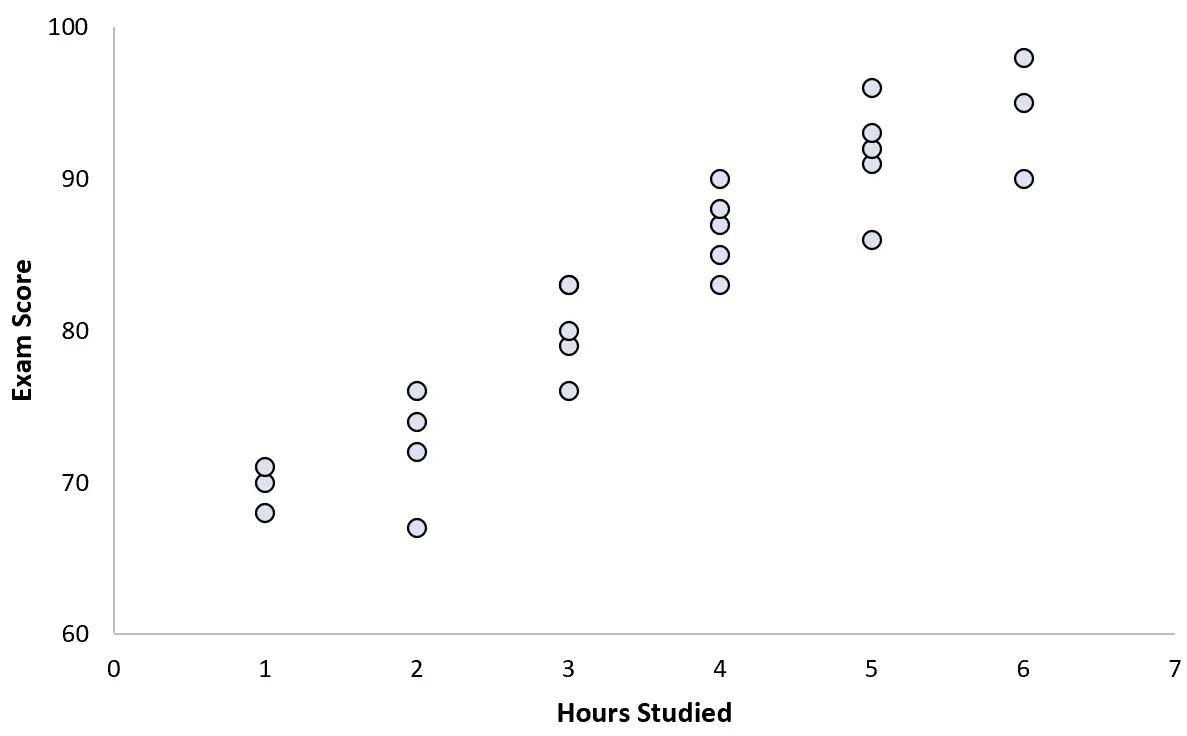
ကိန်းရှင်နှစ်ခုကြားတွင် ရှင်းရှင်းလင်းလင်း အပြုသဘောဆောင်သော ဆက်စပ်မှုရှိသည်။ လေ့လာချိန်နာရီအရေအတွက်များလာသည်နှင့်အမျှ စာမေးပွဲရမှတ်သည် မျှမျှတတ ခန့်မှန်းနိုင်သောနှုန်းဖြင့် တိုးလာသည်။

ထို့နောက် သူသည် တုံ့ပြန်မှုကိန်းရှင်အဖြစ် ခန့်မှန်းတွက်ချက်မှုကိန်းရှင်နှင့် နောက်ဆုံးစာမေးပွဲအဆင့်အဖြစ် လေ့လာထားသော နာရီများကို အသုံးပြု၍ ရိုးရှင်းသောမျဉ်းကြောင်းဆုတ်ယုတ်မှုပုံစံကို အံကိုက်ပြုလုပ်သည်။

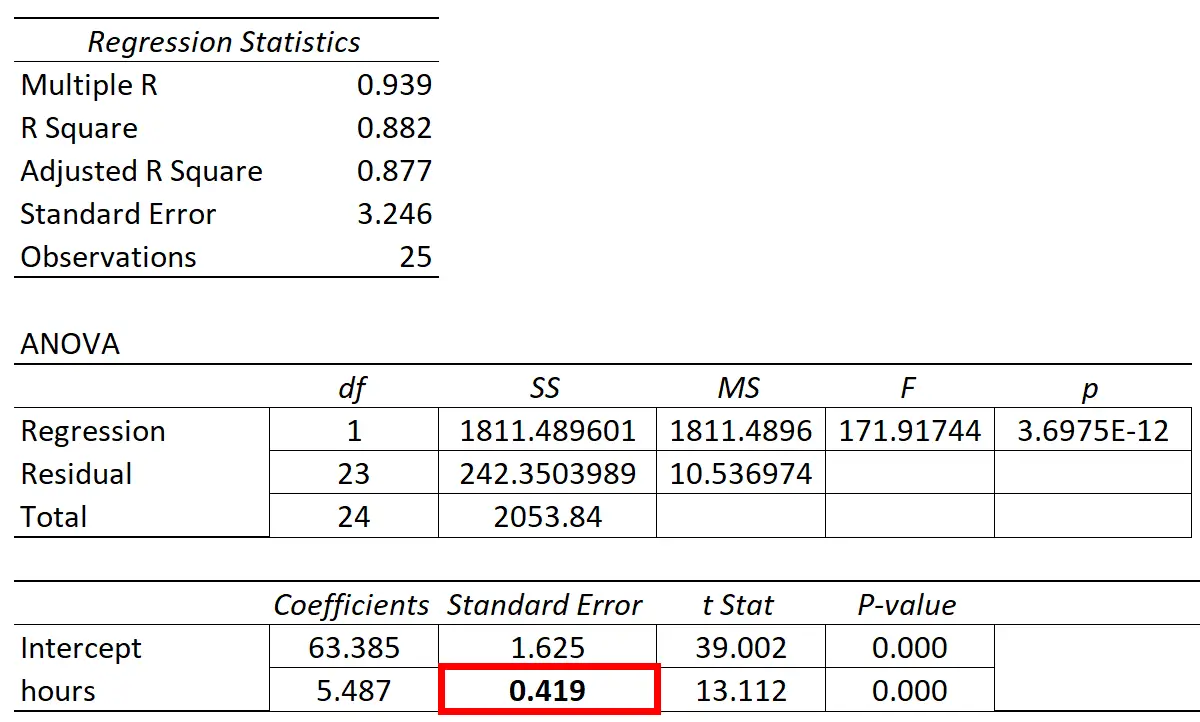
အောက်ပါဇယားသည် ဆုတ်ယုတ်မှုရလဒ်များကို ပြသသည်-

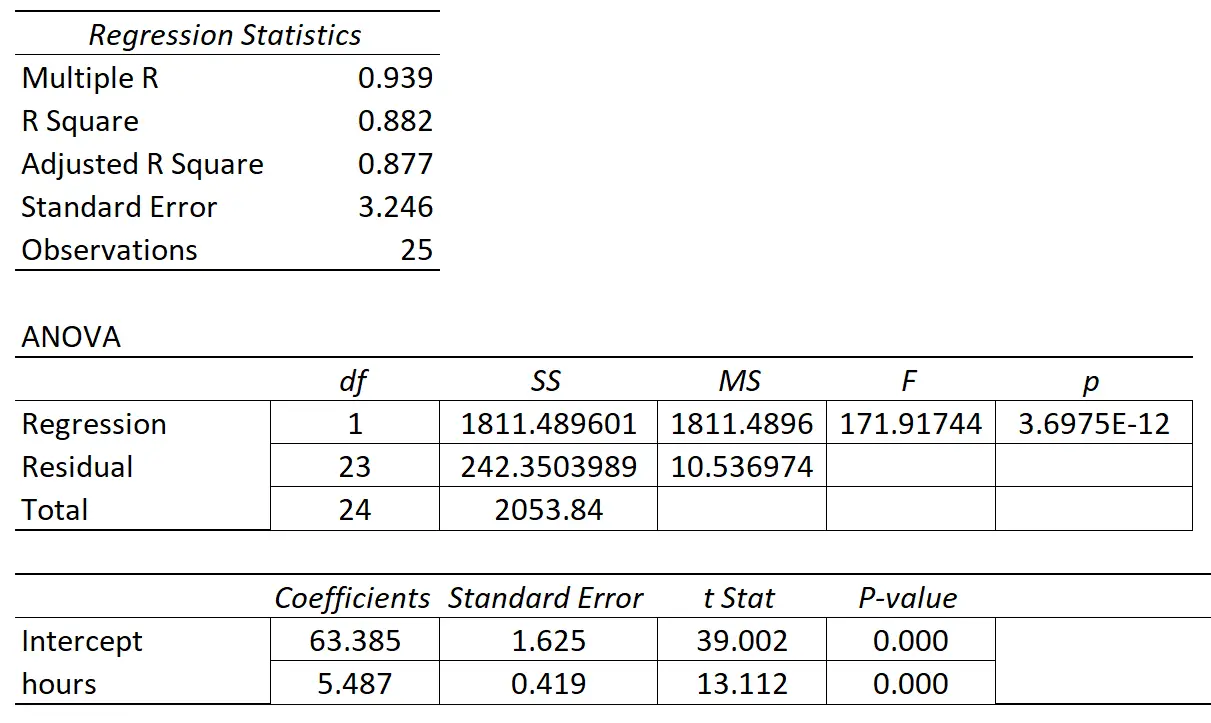
ခန့်မှန်းတွက်ချက်နိုင်သောကိန်းရှင် “ လေ့လာမှုနာရီ” ၏ကိန်းဂဏန်းသည် 5.487 ဖြစ်သည်။ ထပ်လောင်းလေ့လာထားသောနာရီတိုင်းသည် စာမေးပွဲရမှတ်တွင် ပျမ်းမျှ 5,487 တိုးလာခြင်းနှင့် ဆက်စပ်နေကြောင်း ၎င်းကဆိုသည်။

စံလွဲချော်မှုမှာ 0.419 ဖြစ်ပြီး၊ ဆုတ်ယုတ်မှု လျှောစောက်အတွက် ဤခန့်မှန်းချက်ပတ်လည် ကွဲပြားမှုအတိုင်းအတာကို ကိုယ်စားပြုသည်။

ခန့်မှန်းသူကိန်းရှင် “နာရီလေ့လာသည်” အတွက် t-statistic ကိုတွက်ချက်ရန် ဤတန်ဖိုးကို ကျွန်ုပ်တို့အသုံးပြုနိုင်သည်-

• t ကိန်းဂဏန်း = ကိန်းဂဏန်း ခန့်မှန်းချက် / စံအမှား
• t-statistic = 5.487 / 0.419
• t-statistic = 13.112

ဤစမ်းသပ်မှုစာရင်းအင်းနှင့် ကိုက်ညီသော p-တန်ဖိုးသည် 0.000 ဖြစ်ပြီး၊ “ လေ့လာခဲ့သည့်နာရီ” သည် နောက်ဆုံးစာမေးပွဲအဆင့်နှင့် စာရင်းအင်းဆိုင်ရာ သိသာထင်ရှားသော ဆက်နွယ်မှုရှိကြောင်း ဖော်ပြသည်။

regression slope ၏ စံလွဲချော်မှုသည် regression slope ၏ coefficient ခန့်မှန်းချက်နှင့် နှိုင်းယှဉ်ပါက သေးငယ်သောကြောင့်၊ ခန့်မှန်းသူ variable သည် ကိန်းဂဏန်းအရ သိသာထင်ရှားပါသည်။

ဥပမာ 2- Regression Slope ၏ ကြီးမားသော စံအမှားကို ဘာသာပြန်ခြင်း။

အခြားပါမောက္ခတစ်ဦးက စာသင်ချိန်နာရီအရေအတွက်နှင့် ၎င်း၏အတန်းရှိ ကျောင်းသားများ၏ နောက်ဆုံးစာမေးပွဲအဆင့်ကြား ဆက်စပ်မှုကို နားလည်လိုသည်ဆိုပါစို့။

သူသည် ကျောင်းသား 25 ဦးအတွက် ဒေတာစုဆောင်းပြီး အောက်ပါ အပိုင်းအစကို ဖန်တီးသည်-

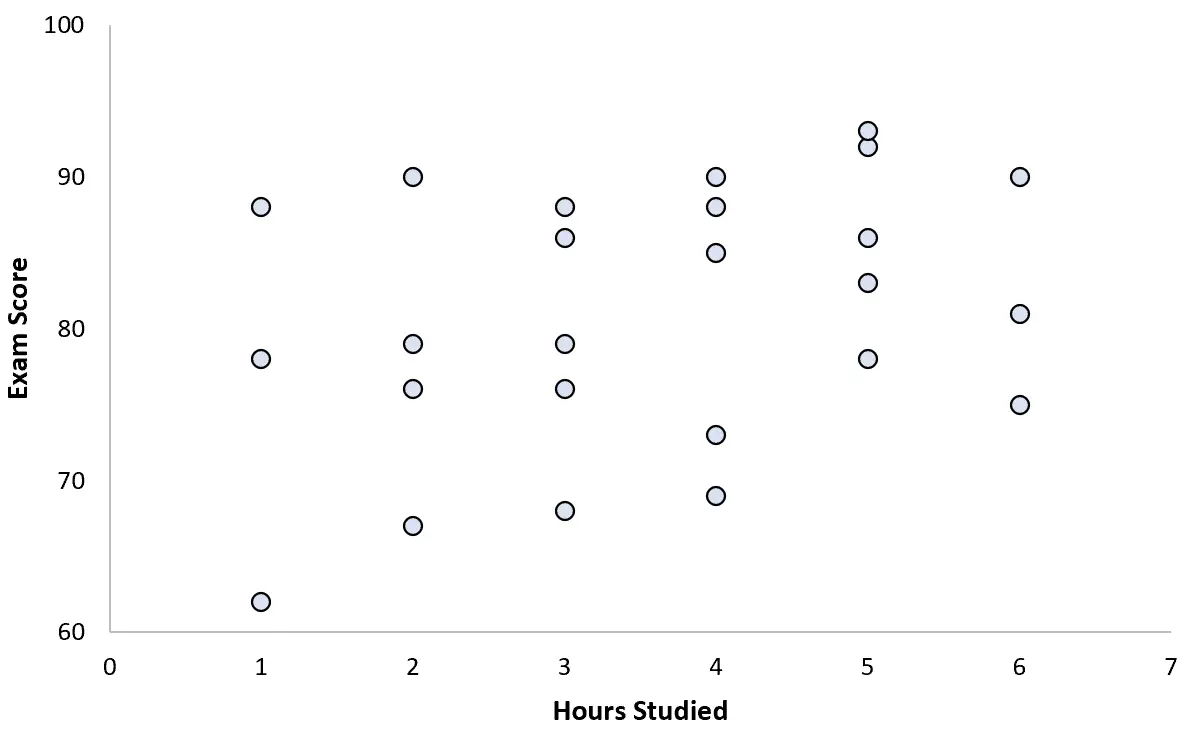
ကိန်းရှင်နှစ်ခုကြားတွင် အနည်းငယ် အပြုသဘောဆောင်သော ဆက်စပ်မှုရှိပုံပေါ်သည်။ စာသင်ချိန်နာရီများ တိုးလာသည်နှင့်အမျှ စာမေးပွဲရမှတ်သည် ယေဘုယျအားဖြင့် တိုးလာသော်လည်း ခန့်မှန်းနိုင်သောနှုန်းဖြင့် မဟုတ်ပါ။

ထို့နောက် ပရော်ဖက်ဆာသည် တုံ့ပြန်မှုကိန်းရှင်အဖြစ် ခန့်မှန်းကိန်းပြောင်းနိုင်သောကိန်းရှင်နှင့် နောက်ဆုံးစာမေးပွဲအဆင့်အဖြစ် လေ့လာထားသော နာရီများကို အသုံးပြု၍ ရိုးရှင်းသောမျဉ်းကြောင်းဆုတ်ယုတ်မှုပုံစံနှင့် ကိုက်ညီသည်ဟု ယူဆပါ။

အောက်ပါဇယားသည် ဆုတ်ယုတ်မှုရလဒ်များကို ပြသသည်-

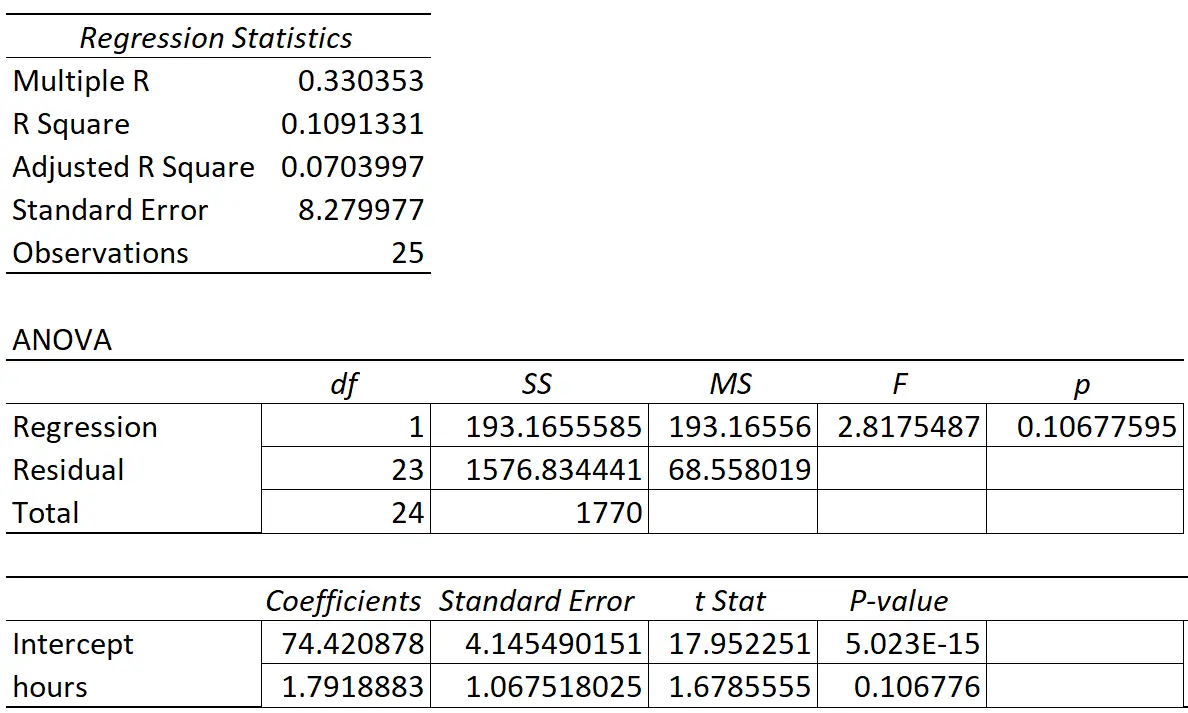
ခန့်မှန်းတွက်ချက်နိုင်သောကိန်းရှင် “ လေ့လာမှုနာရီ” ၏ကိန်းဂဏန်းသည် 1.7919 ဖြစ်သည်။ လေ့လာမှုတစ်ခုစီသည် စာမေးပွဲရမှတ်တွင် ပျမ်းမျှ 1.7919 တိုးလာခြင်းနှင့် ဆက်စပ်နေကြောင်း ၎င်းက ကျွန်ုပ်တို့အား ပြောပြသည်။

စံလွဲချော်မှုမှာ 1.0675 ဖြစ်ပြီး၊ ဆုတ်ယုတ်မှု လျှောစောက်အတွက် ဤခန့်မှန်းချက်ပတ်လည် ကွဲပြားမှု၏ အတိုင်းအတာတစ်ခုဖြစ်သည်။

ခန့်မှန်းသူကိန်းရှင် “နာရီလေ့လာသည်” အတွက် t-statistic ကိုတွက်ချက်ရန် ဤတန်ဖိုးကို ကျွန်ုပ်တို့အသုံးပြုနိုင်သည်-

• t ကိန်းဂဏန်း = ကိန်းဂဏန်း ခန့်မှန်းချက် / စံအမှား
• t-statistic = 1.7919 / 1.0675
• t-statistic = 1.678

ဤစမ်းသပ်မှုစာရင်းအင်းနှင့် ကိုက်ညီသော p-တန်ဖိုးသည် 0.107 ဖြစ်သည်။ ဤ p-value သည် 0.05 ထက်မနည်းသောကြောင့်၊ ၎င်းသည် “ လေ့လာခဲ့သောနာရီများ” သည် နောက်ဆုံးစာမေးပွဲအဆင့်နှင့် စာရင်းအင်းဆိုင်ရာ သိသာထင်ရှားသော ဆက်နွယ်မှုမရှိကြောင်း ညွှန်ပြနေသည်။

regression slope ၏ standard error သည် regression slope ၏ coefficient ခန့်မှန်းချက်နှင့် နှိုင်းယှဉ်လျှင် ကြီးမားသောကြောင့်၊ ခန့်မှန်းသူ variable သည် ကိန်းဂဏန်းအရ သိသာထင်ရှားခြင်း မရှိပါ ။

ထပ်လောင်းအရင်းအမြစ်များ

Simple Linear Regression နိဒါန်း
Multiple Linear Regression အကြောင်း နိဒါန်း
Regression Table ကို ဘယ်လိုဖတ်ပြီး အဓိပါယ်ရမလဲ