Excel တွင် odds ratio နှင့် relative risk တွက်ချက်နည်း

အောက်ပါဖော်မတ်ကို ယူသည့် ဇယား 2 နှင့် 2 တွင် ခွဲခြမ်းစိတ်ဖြာမှုလုပ်ဆောင်သည့်အခါ လေးနက်မှုအချိုး နှင့် နှိုင်းယှဥ်အန္တရာယ်ကို ကျွန်ုပ်တို့ အသုံးပြုလေ့ရှိသည်-

ထူးထူးခြားခြား အချိုးသည် ကုသမှုအုပ်စုတွင် ဖြစ်ပျက်သည့် ဖြစ်ရပ်တစ်ခု၏ ဖြစ်နိုင်ခြေနှင့် ထိန်းချုပ်မှုအုပ်စုတွင် ဖြစ်ပျက်သည့် ဖြစ်ရပ်တစ်ခု ဖြစ်နိုင်ခြေကြားအချိုးကို ပြောပြသည်။ အောက်ပါအတိုင်း တွက်ချက်သည်။

အတိုးနှုန်းအချိုး = (A*D) / (B*C)

ဆက်စပ်အန္တရာယ်သည် ကုသမှုအုပ်စုတစ်ခုတွင် ဖြစ်ပွားနိုင်ခြေနှင့် ထိန်းချုပ်မှုအုပ်စုတွင် ဖြစ်ပွားသည့် အဖြစ်အပျက်တစ်ခု၏ ဖြစ်နိုင်ခြေကြားအချိုးကို ကျွန်ုပ်တို့အား ပြောပြသည်။ အောက်ပါအတိုင်း တွက်ချက်သည်။

ဆက်စပ်အန္တရာယ် = [A/(A+B)] / [C/(C+D)]

ဤသင်ခန်းစာသည် Excel တွင် odds ratios နှင့် relative risk ကို တွက်ချက်နည်းကို ရှင်းပြထားသည်။

အလေးသာမှုအချိုးနှင့် နှိုင်းယှဥ်နိုင်ခြေကို တွက်ချက်နည်း

ဘတ်စကတ်ဘောကစားသမား ၅၀ သည် လေ့ကျင့်ရေးအစီအစဉ်အသစ်ကို အသုံးပြုနေပြီး ကစားသမား ၅၀ သည် လေ့ကျင့်ရေးအစီအစဉ်ဟောင်းကို အသုံးပြုနေသည်ဆိုပါစို့။ ပရိုဂရမ်၏အဆုံးတွင်၊ ကစားသမားတစ်ဦးစီသည် ကျွမ်းကျင်မှုစမ်းသပ်မှုတစ်ခုကို ဖြေဆိုအောင်မြင်ကြောင်း သိရှိရန် ကျွန်ုပ်တို့ စမ်းသပ်သည်။

အောက်ပါဇယားတွင် ၎င်းတို့အသုံးပြုခဲ့သည့် ပရိုဂရမ်အပေါ်အခြေခံ၍ အောင်မြင်ပြီး ကျရှုံးခဲ့သော ကစားသမားအရေအတွက်ကို ပြသသည်-

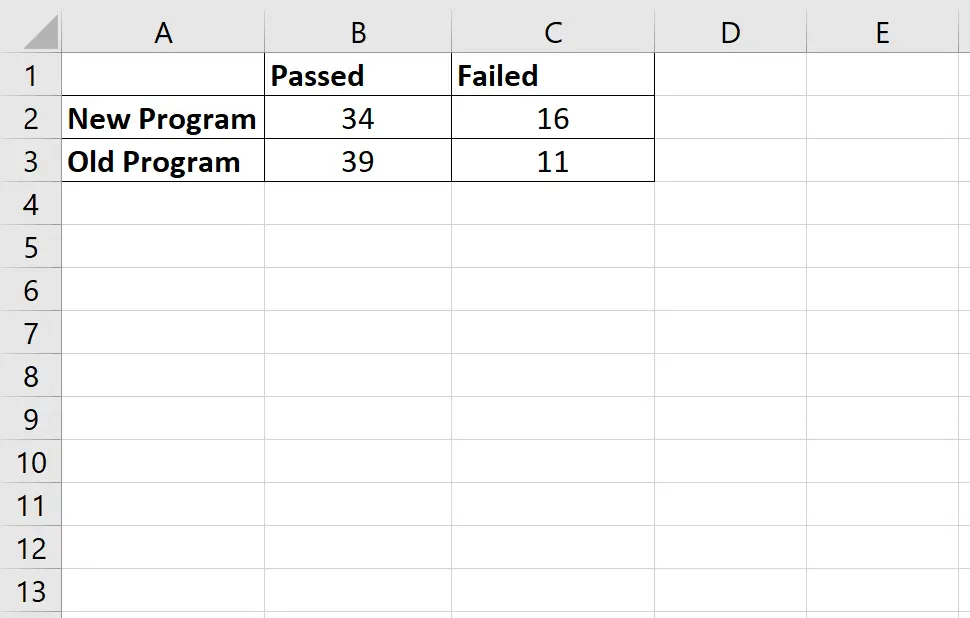
လေးနက်မှုအချိုးကို အောက်ပါအတိုင်း တွက်ချက်သည်- (34*11) / (16*39) = 0.599

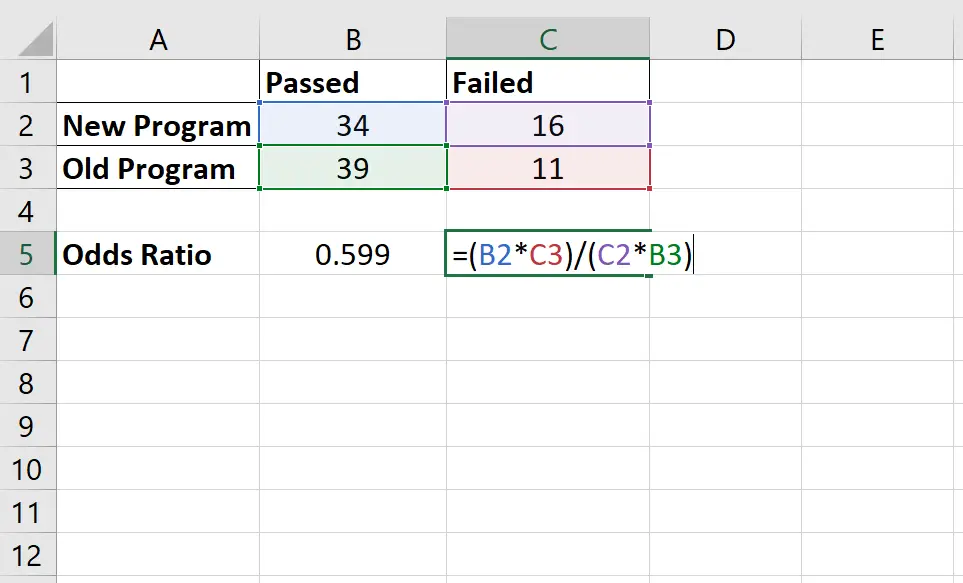
ပရိုဂရမ်အသစ်ကို အသုံးပြု၍ ပရိုဂရမ်အသစ်ကို အသုံးပြု၍ ကစားသမားတစ်ဦး စမ်းသပ်အောင်မြင်နိုင်ခြေသည် ပရိုဂရမ်ဟောင်းကို အသုံးပြု၍ စာမေးပွဲအောင်မြင်သည့် ကစားသမားတစ်ဦး၏ အခွင့်အလမ်း 0.599 ဆ မျှသာဖြစ်သည်ဟု ဆိုလိုခြင်းဖြစ်သည်။

တစ်နည်းဆိုရသော်၊ ပရိုဂရမ်အသစ်ကြောင့် ကစားသမားတစ်ဦး စမ်းသပ်မှုအောင်မြင်ရန် အခွင့်အလမ်းကို အမှန်တကယ် 40.1% လျှော့ချထားသည်။

ဆက်စပ်အန္တရာယ်ကို အောက်ပါအတိုင်း တွက်ချက်သည်- [34/(34+16)] / [39/(39+11)] = 0.872

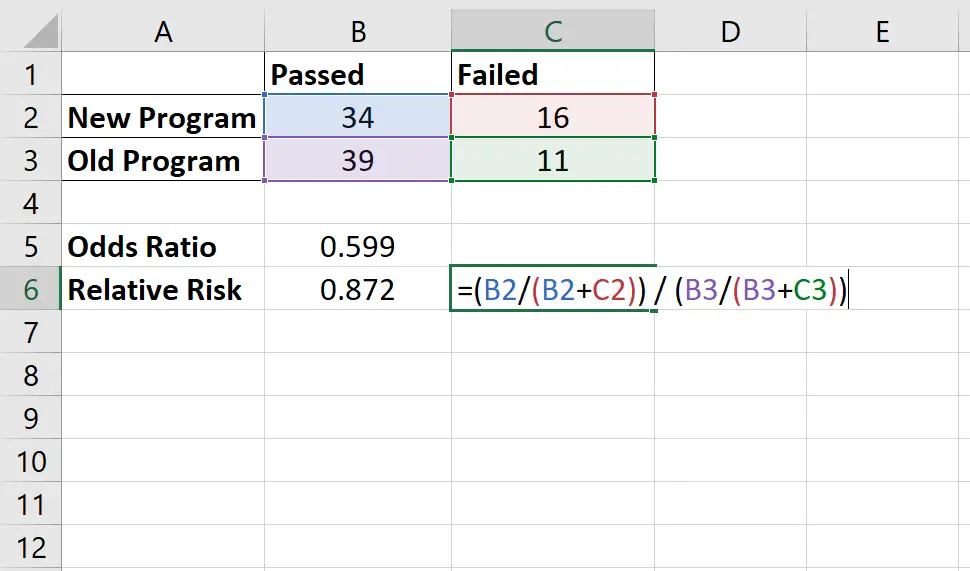
ပရိုဂရမ်အသစ်ကို အသုံးပြု၍ ပရိုဂရမ်ဟောင်းနှင့် ပရိုဂရမ်ဟောင်းကို အသုံးပြု၍ စမ်းသပ်မှုအောင်မြင်သည့် ကစားသမားတစ်ဦး၏ ဖြစ်နိုင်ခြေအချိုးသည် 0.872 ဖြစ်သည်ဟု ဆိုလိုခြင်းဖြစ်သည်ဟု ကျွန်ုပ်တို့အဓိပ္ပာယ်ဖွင့်ဆိုလိုပါသည်။

ဤတန်ဖိုးသည် 1 ထက်နည်းသောကြောင့်၊ ၎င်းသည် ပရိုဂရမ်အသစ်တွင် ပရိုဂရမ်ဟောင်းထက် ပရိုဂရမ်အသစ်တွင် အမှန်တကယ်အောင်မြင်နိုင်ခြေနည်းပါးကြောင်း ညွှန်ပြနေသည်။

ပရိုဂရမ်တစ်ခုစီအောက်တွင် ကစားသမားတစ်ဦးဖြတ်သန်းသွားမည့် ဖြစ်နိုင်ခြေကို တိုက်ရိုက်တွက်ချက်ခြင်းဖြင့်လည်း ၎င်းကို ကျွန်ုပ်တို့ တွေ့မြင်နိုင်သည်-

အစီအစဉ်သစ်အရ အောင်မြင်နိုင်ခြေ = 34/50 = 68%

ပရိုဂရမ်ဟောင်းအရ အောင်မြင်နိုင်ခြေ = 39/50 = 78%

ယုံကြည်မှုကြားကာလကို ဘယ်လိုတွက်မလဲ။

ကျွန်ုပ်တို့သည် မသာမယာအချိုးနှင့် နှိုင်းယှဥ်အန္တရာယ်ကို တွက်ချက်ပြီးသည်နှင့်၊ ဤအစီအမံနှစ်ခုအတွက် ယုံကြည်မှုကြားကာလများကို တွက်ချက်ရန်လည်း ကျွန်ုပ်တို့ စိတ်ဝင်စားပေမည်။

ကွဲလွဲမှုအချိုး အတွက် 95% ယုံကြည်မှုကြားကာလကို အောက်ပါဖော်မြူလာကို အသုံးပြု၍ တွက်ချက်နိုင်ပါသည်။

အချိုးမညီမှုအတွက် 95% CI = [ e^(ln(OR) – 1.96*SE(ln(OR))), e^(ln(OR) – 1.96*SE(ln(OR) ))]

SE(ln(OR)) =√ 1/A + 1/B + 1/C + 1/D နေရာတွင်

အလေးသာအချိုးအတွက် 95% CI သည် (0.245၊ 1.467) ဖြစ်သည်ကို တွေ့ရှိခဲ့သည်။ အောက်ဖော်ပြပါပုံသည် ဤယုံကြည်မှုကြားကာလကို တွက်ချက်ရန် ကျွန်ုပ်တို့အသုံးပြုသည့် ဖော်မြူလာကို ပြသသည်-

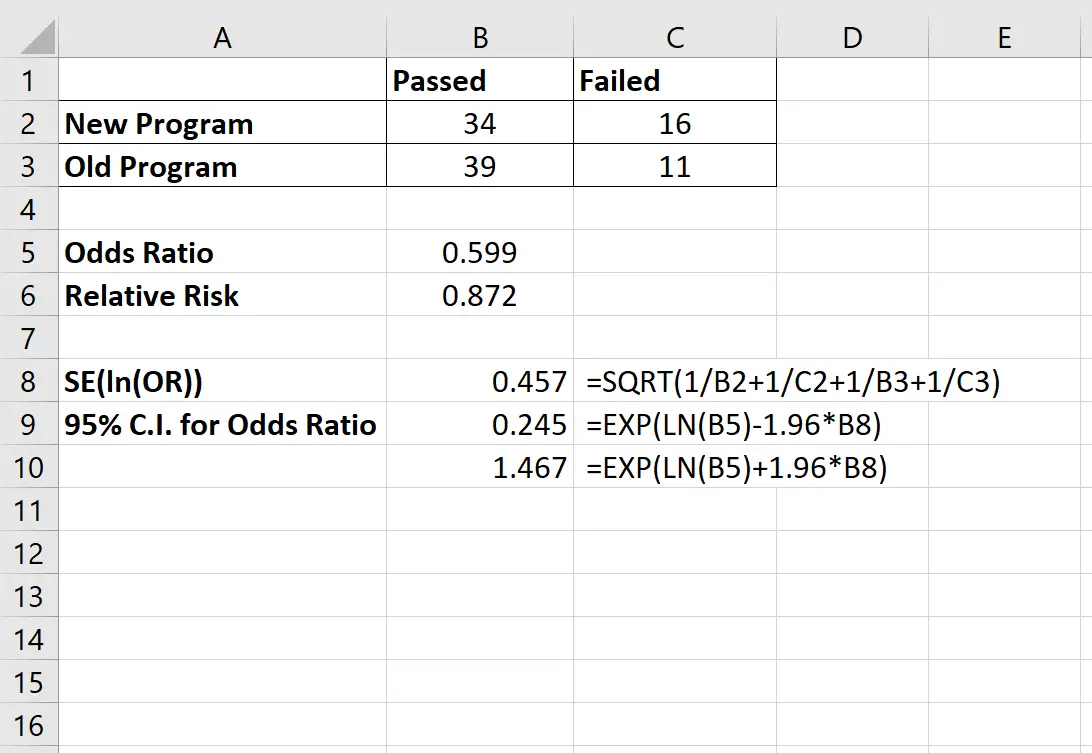
ဆက်စပ်အန္တရာယ် အတွက် 95% ယုံကြည်မှုကြားကာလကို အောက်ပါဖော်မြူလာကို အသုံးပြု၍ တွက်ချက်နိုင်ပါသည်။

ဆက်စပ်အန္တရာယ်အတွက် 95% CI = exp(ln(RR) – 1.96*SE(ln(RR)))) မှ exp(ln(RR) – 1.96*SE(ln(RR))))

SE(ln(RR)) =√ 1/A + 1/C – 1/(A+B) – 1/(C+D)

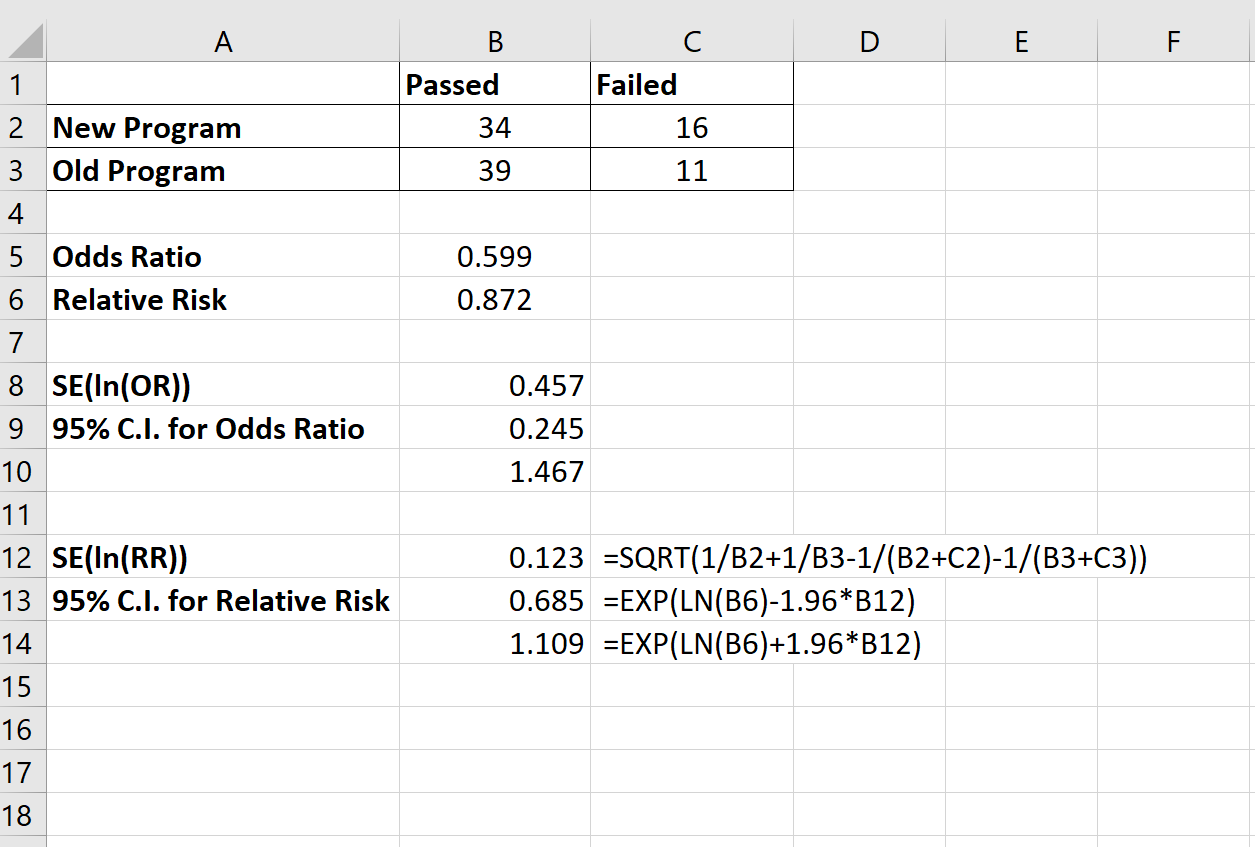
ဆက်စပ်အန္တရာယ်အတွက် 95% CI သည် (0.685၊ 1.109) ဖြစ်သည်ကို တွေ့ရှိခဲ့သည်။ အောက်ဖော်ပြပါပုံသည် ဤယုံကြည်မှုကြားကာလကို တွက်ချက်ရန် ကျွန်ုပ်တို့အသုံးပြုသည့် ဖော်မြူလာကို ပြသသည်-

ထပ်လောင်းအရင်းအမြစ်များ

အောက်ဖော်ပြပါ သင်ခန်းစာများတွင် ထူးထူးခြားခြား အချိုးများနှင့် နှိုင်းယှဥ်နိုင်ခြေကို အဓိပ္ပာယ်ပြန်ဆိုပုံဆိုင်ရာ နောက်ထပ်အချက်အလက်များကို ပေးဆောင်သည်-

ထူးထူးခြားခြား အချိုးတွေကို ဘယ်လိုအဓိပ္ပာယ်ဖွင့်မလဲ။
နှိုင်းရအန္တရာယ်ကို ဘယ်လိုအဓိပ္ပာယ်ဖွင့်မလဲ။