Rmse နှင့် r-squared- မည်သည့် metric ကို သင်အသုံးပြုသင့်သနည်း။

ဆုတ်ယုတ်မှုပုံစံများကို တစ်ခု သို့မဟုတ် တစ်ခုထက်ပိုသော ကြိုတင်ခန့်မှန်းကိန်းရှင်များနှင့် တုံ့ပြန်မှုကိန်းရှင်တစ်ခုအကြား ဆက်နွယ်မှုကို အရေအတွက်သတ်မှတ်ရန်အတွက် အသုံးပြုသည်။

ကျွန်ုပ်တို့သည် ဆုတ်ယုတ်မှုပုံစံတစ်ခုကို အံဝင်ခွင်ကျဖြစ်စေသည့်အခါတိုင်း၊ မော်ဒယ်သည် ဒေတာနှင့် မည်မျှကိုက်ညီကြောင်း နားလည်လိုပါသည်။ တစ်နည်းဆိုရသော် တုံ့ပြန်မှုကိန်း ရှင်၏တန်ဖိုးကို ခန့်မှန်းရန် မော်ဒယ်သည် ခန့်မှန်းသူကိန်းရှင်များ၏ တန်ဖိုးများကို မည်မျှကောင်းစွာအသုံးပြုနိုင်သနည်း။

စာရင်းအင်းပညာရှင်များက ဒေတာအတွဲတစ်ခုနှင့် ကိုက်ညီမှုရှိမရှိကို တွက်ချက်ရန်အတွက် စာရင်းအင်းပညာရှင်များအသုံးပြုလေ့ရှိသည့် မက်ထရစ်နှစ်ခုမှာ အောက်ပါအတိုင်းတွက်ချက်ထားသည့် root mean square error (RMSE) နှင့် R နှစ်ထပ်ကိန်း ( ^R2 ) ဖြစ်သည်-

RMSE : ပျမ်းမျှအားဖြင့် ဒေတာအတွဲတစ်ခုရှိ ခန့်မှန်းထားသော တန်ဖိုးများမှ မည်မျှဝေးသည်ကို ပြောပြသော မက်ထရစ်တစ်ခု။ RMSE နိမ့်လေ၊ မော်ဒယ်တစ်ခုသည် ဒေတာအစုံနှင့် ကိုက်ညီလေလေဖြစ်သည်။

အောက်ပါအတိုင်း တွက်ချက်သည်။

RMSE = √ Σ(P _i – O _i ) ² / n

ရွှေ-

• ∑ သည် “ပေါင်း” ဟူသော သင်္ကေတတစ်ခုဖြစ်သည်။
• P _i သည် ^IT Observation အတွက် ခန့်မှန်းတန်ဖိုးဖြစ်သည်။
• O _i သည် ^ith observation အတွက် မှတ်သားထားသော တန်ဖိုးဖြစ်သည်။
• n သည် နမူနာအရွယ်အစားဖြစ်သည်။

R ² : ဆုတ်ယုတ်မှုပုံစံတစ်ခု၏ တုံ့ပြန်မှုကိန်းရှင်တွင် ကွဲလွဲမှုမည်မျှရှိသည်ကို ပြောပြသော မက်ထရစ်တစ်ခုသည် ကြိုတင်ခန့်မှန်းကိန်းရှင်များဖြင့် ရှင်းပြနိုင်သည်။ ဤတန်ဖိုးသည် 0 နှင့် 1 အကြားဖြစ်သည်။ R ² တန်ဖိုးမြင့်လေ၊ မော်ဒယ်သည် ဒေတာအစုအဝေးနှင့် ကိုက်ညီလေလေဖြစ်သည်။

အောက်ပါအတိုင်း တွက်ချက်သည်။

^R2 = 1 – (RSS/TSS)

ရွှေ-

• RSS သည် အကြွင်းအကျန်များ၏ နှစ်ထပ်ကိန်းများကို ကိုယ်စားပြုသည်။
• TSS သည် စုစုပေါင်းစတုရန်းများကိုကိုယ်စားပြုသည်။

RMSE နှင့် R ² − မည်သည့် Metric ကို သင်အသုံးပြုသင့်သနည်း။

ဒေတာအတွဲတစ်ခုအတွက် မော်ဒယ်တစ်ခု၏ အံဝင်ခွင်ကျမှုကို အကဲဖြတ်သည့်အခါ၊ မက်ထရစ်တစ်ခုစီသည် ကျွန်ုပ်တို့အား မတူညီသည့်အရာများကို ပြောပြသောကြောင့် RMSE တန်ဖိုးနှင့် R ² တန်ဖိုး နှစ်ခု လုံး ကို တွက်ချက်ရန် အသုံးဝင်ပါသည်။

တစ်ဖက်တွင်၊ RMSE သည် ဆုတ်ယုတ်မှုပုံစံဖြင့် ပြုလုပ်ထားသော ခန့်မှန်းတန်ဖိုးနှင့် တန်ဖိုးအမှန်အကြား ပုံမှန်အကွာအဝေးကို ပြောပြသည်။

အခြားတစ်ဖက်တွင်၊ R ² သည် တုံ့ပြန်မှုကိန်းရှင်၏ ကွဲလွဲမှုကို ရှင်းပြနိုင်သည့်အတိုင်းအတာကို ခန့်မှန်းပေးသည်။

ဥပမာအားဖြင့်၊ ကျွန်ုပ်တို့တွင် မြို့တစ်မြို့ရှိ အိမ်များအကြောင်း အချက်အလက်များကို ဖော်ပြသည့် အောက်ပါဒေတာအတွဲရှိသည် ဆိုပါစို့။

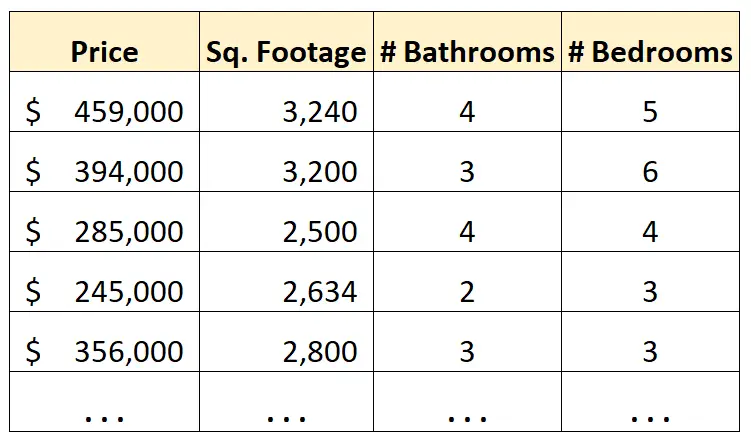
အိမ်တစ်အိမ်၏စျေးနှုန်းကို ခန့်မှန်းရန် ယခု ကျွန်ုပ်တို့သည် စတုရန်းပေ၊ ရေချိုးခန်းအရေအတွက်နှင့် အိပ်ခန်းအရေအတွက်တို့ကို အသုံးပြုလိုသည်ဆိုကြပါစို့။

အောက်ဖော်ပြပါ ဆုတ်ယုတ်မှုပုံစံကို ကျွန်ုပ်တို့ လိုက်လျောညီထွေဖြစ်အောင် လုပ်ဆောင်နိုင်သည်-

ဈေးနှုန်း = β ₀ + β ₁ (စတုရန်းပုံ) + β ₂ ( # ရေချိုးခန်း ) + β ₃ ( # အိပ်ခန်း )

ယခု ကျွန်ုပ်တို့သည် ဤမော်ဒယ်နှင့် အံကိုက်ဖြစ်ပြီး မော်ဒယ်၏ အံဝင်ခွင်ကျ ကောင်းမွန်မှုကို အကဲဖြတ်ရန် အောက်ပါ မက်ထရစ်များကို တွက်ချက်မည်ဆိုပါစို့။

• RMSE : 14.342
• ^R2 : 0.856

RMSE တန်ဖိုးသည် မော်ဒယ်၏ ခန့်မှန်းထားသော အိမ်စျေးနှုန်းနှင့် အမှန်တကယ်အိမ်ပေါက်ဈေးအကြား ပျမ်းမျှကွာခြားချက်မှာ $14,342 ဖြစ်ကြောင်း ကျွန်ုပ်တို့ကို ပြောပြသည်။

R ² တန်ဖိုးသည် မော်ဒယ်၏ ကြိုတင်ခန့်မှန်းကိန်းရှင်များ (စတုရန်းပုံ၊ ရေချိုးခန်း အရေအတွက်နှင့် အိပ်ခန်းအရေအတွက်) သည် အိမ်ရာစျေးနှုန်းများ ကွဲလွဲမှု၏ 85.6% ကို ရှင်းပြနိုင်သည်ဟု ကျွန်ုပ်တို့ကို ပြောပြသည်။

ဤတန်ဖိုးများသည် “ကောင်းသည်” ရှိ၊ မရှိ ဆုံးဖြတ်ရန်၊ ဤတိုင်းတာမှုများကို အခြားပုံစံများနှင့် နှိုင်းယှဉ်နိုင်သည်။

ဥပမာအားဖြင့်၊ ကျွန်ုပ်တို့သည် မတူညီသော ကြိုတင်ခန့်မှန်းကိန်းရှင်များကို အသုံးပြုပြီး ထိုမော်ဒယ်အတွက် အောက်ဖော်ပြပါ မက်ထရစ်များကို တွက်ချက်သည့် အခြားသော ဆုတ်ယုတ်မှုပုံစံနှင့် ကိုက်ညီသည်ဆိုပါစို့။

• RMSE : 19,355
• ^R2 : 0.765

ဤမော်ဒယ်၏ RMSE တန်ဖိုးသည် ယခင်မော်ဒယ်ထက် ပိုမိုမြင့်မားသည်ကို ကျွန်ုပ်တို့တွေ့မြင်နိုင်ပါသည်။ ဤမော်ဒယ်၏ R ² တန်ဖိုးသည် ယခင်မော်ဒယ်ထက် နိမ့်ကြောင်းကိုလည်း တွေ့မြင်နိုင်သည်။ ၎င်းသည် ဤမော်ဒယ်သည် ယခင်မော်ဒယ်ထက် ဒေတာနှင့် အံဝင်ခွင်ကျမဖြစ်ကြောင်း ကျွန်ုပ်တို့ကိုပြောပြသည်။

အကျဉ်းချုပ်

ဤဆောင်းပါးတွင် ဖော်ပြထားသော အဓိကအချက်များမှာ အောက်ပါအတိုင်းဖြစ်သည်။

• RMSE နှင့် R ² သည် ဆုတ်ယုတ်မှုပုံစံသည် ဒေတာအစုံနှင့် မည်မျှကိုက်ညီကြောင်း တွက်ချက်သည်။
• RMSE သည် ဆုတ်ယုတ်မှုပုံစံတစ်ခုသည် တုံ့ပြန်မှုကိန်းရှင်၏တန်ဖိုးကို အကြွင်းမဲ့အသုံးအနှုန်းများဖြင့် ခန့်မှန်းနိုင်သော်လည်း R ² သည် မော်ဒယ်တစ်ခုသည် ရာခိုင်နှုန်းသတ်မှတ်ချက်များတွင် တုံ့ပြန်မှုကိန်းရှင်၏တန်ဖိုးကို မည်မျှကောင်းစွာခန့်မှန်းနိုင်သည်ကို ပြောပြသည်။
• မက်ထရစ်တစ်ခုစီသည် ကျွန်ုပ်တို့အား အသုံးဝင်သောအချက်အလက်များပေးသောကြောင့် ပေးထားသောမော်ဒယ်အတွက် RMSE နှင့် ^R2 နှစ်ခုလုံးကို တွက်ချက်ရန် အသုံးဝင်ပါသည်။

ထပ်လောင်းအရင်းအမြစ်များ

Multiple Linear Regression အကြောင်း နိဒါန်း
R နှင့် R-Square- ကွာခြားချက်ကား အဘယ်နည်း။
ကောင်းသော R-squared တန်ဖိုးဆိုသည်မှာ အဘယ်နည်း။