Root mean square error (rmse) ကို ဘယ်လိုအဓိပ္ပာယ်ဖွင့်မလဲ

Regression analysis သည် တစ်ခု သို့မဟုတ် တစ်ခုထက်ပိုသော ကြိုတင်ခန့်မှန်းကိန်းရှင်များနှင့် တုံ့ပြန်မှု variable အကြား ဆက်နွယ်မှုကို နားလည်ရန် ကျွန်ုပ်တို့ အသုံးပြုနိုင်သည့် နည်းလမ်းတစ်ခုဖြစ်သည်။

ဆုတ်ယုတ်မှုပုံစံတစ်ခုသည် ဒေတာအတွဲတစ်ခုနှင့် ကိုက်ညီမှုရှိမရှိကို အကဲဖြတ်ရန် နည်းလမ်းတစ်ခုမှာ မော်ဒယ်၏ခန့်မှန်းတန်ဖိုးများနှင့် ဒေတာအတွဲ၏ အမှန်တကယ်တန်ဖိုးများကြားရှိ ပျမ်းမျှအကွာအဝေးကို ပြောပြသည့် မက်ထရစ်တစ်ခုဖြစ်သည့် ပျမ်းမျှနှစ်ထပ်အမှားကို တွက်ချက်ခြင်းဖြစ်သည်။

RMSE နိမ့်လေ၊ ပေးထားသော မော်ဒယ်သည် ဒေတာအစုံကို “အံကိုက်” လုပ်နိုင်လေဖြစ်သည်။

ပျမ်းမျှစတုရန်းအမှားကို ရှာဖွေရန် ဖော်မြူလာ၊ မကြာခဏ အတိုကောက် RMSE သည်-

RMSE = √ Σ(P _i – O _i ) ² / n

ရွှေ-

• ∑ သည် “ပေါင်း” ဟု အဓိပ္ပါယ်ရသော ဖန်စီသင်္ကေတတစ်ခုဖြစ်သည်။
• P _i သည် dataset ရှိ ^ith observation အတွက် ခန့်မှန်းထားသော တန်ဖိုးဖြစ်သည်။
• O _i သည် dataset အတွင်းရှိ ^ith observation အတွက် သတိပြုမိသောတန်ဖိုးဖြစ်သည်။
• n သည် နမူနာအရွယ်အစားဖြစ်သည်။

အောက်ဖော်ပြပါ ဥပမာသည် ပေးထားသော ဆုတ်ယုတ်မှုပုံစံအတွက် RMSE ကို မည်သို့အဓိပ္ပာယ်ဖွင့်ဆိုသည်ကို ပြသထားသည်။

ဥပမာ- ဆုတ်ယုတ်မှုပုံစံအတွက် RMSE ကို ဘယ်လိုအဓိပ္ပာယ်ဖွင့်မလဲ။

ကောလိပ်ဝင်ခွင့်စာမေးပွဲတွင် ကျောင်းသားများ၏ “ စာမေးပွဲအဆင့်” ကို ခန့်မှန်းရန် “ နာရီများလေ့လာထားသည်” ကို အသုံးပြု၍ ဆုတ်ယုတ်မှုပုံစံကို တည်ဆောက်လိုသည်ဆိုပါစို့။

ကျောင်းသား 15 ယောက်အတွက် အောက်ပါအချက်အလက်များကို ကျွန်ုပ်တို့စုဆောင်းပါသည်။

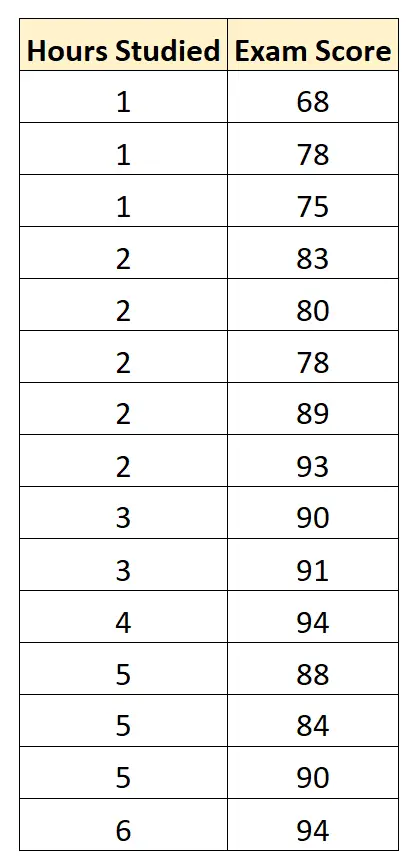
ထို့နောက် ကျွန်ုပ်တို့သည် စာရင်းအင်းဆော့ဖ်ဝဲ (Excel၊ SPSS၊ R၊ Python) စသည်တို့ကို အသုံးပြုပါသည်။ အောက်ပါ တပ်ဆင်ထားသော ဆုတ်ယုတ်မှုပုံစံကို ရှာဖွေရန်-

စာမေးပွဲရမှတ် = 75.95 + 3.08* (စာသင်ချိန်)

ထို့နောက် ကျောင်းသားတစ်ဦးစီ၏ စာမေးပွဲရမှတ်ကို ခန့်မှန်းရန် ဤညီမျှခြင်းအား ၎င်းတို့လေ့လာခဲ့သည့် နာရီအရေအတွက်ပေါ် မူတည်၍ ကျွန်ုပ်တို့အသုံးပြုနိုင်သည်-

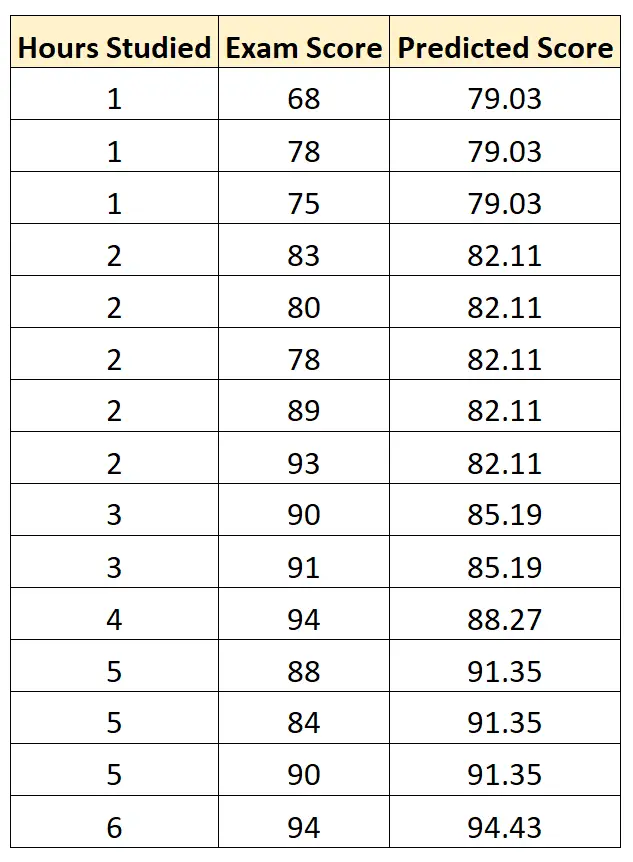
ထို့နောက် ခန့်မှန်းထားသော စာမေးပွဲရမှတ်တစ်ခုစီနှင့် အမှန်တကယ် စာမေးပွဲရမှတ်ကြား နှစ်ထပ်ကိန်းခြားနားချက်ကို ကျွန်ုပ်တို့ တွက်ချက်နိုင်ပါသည်။ ထို့နောက် ဤကွဲပြားမှုများ၏ ပျမ်းမျှနှစ်ထပ်ကိန်းကို ကျွန်ုပ်တို့ယူနိုင်သည်-

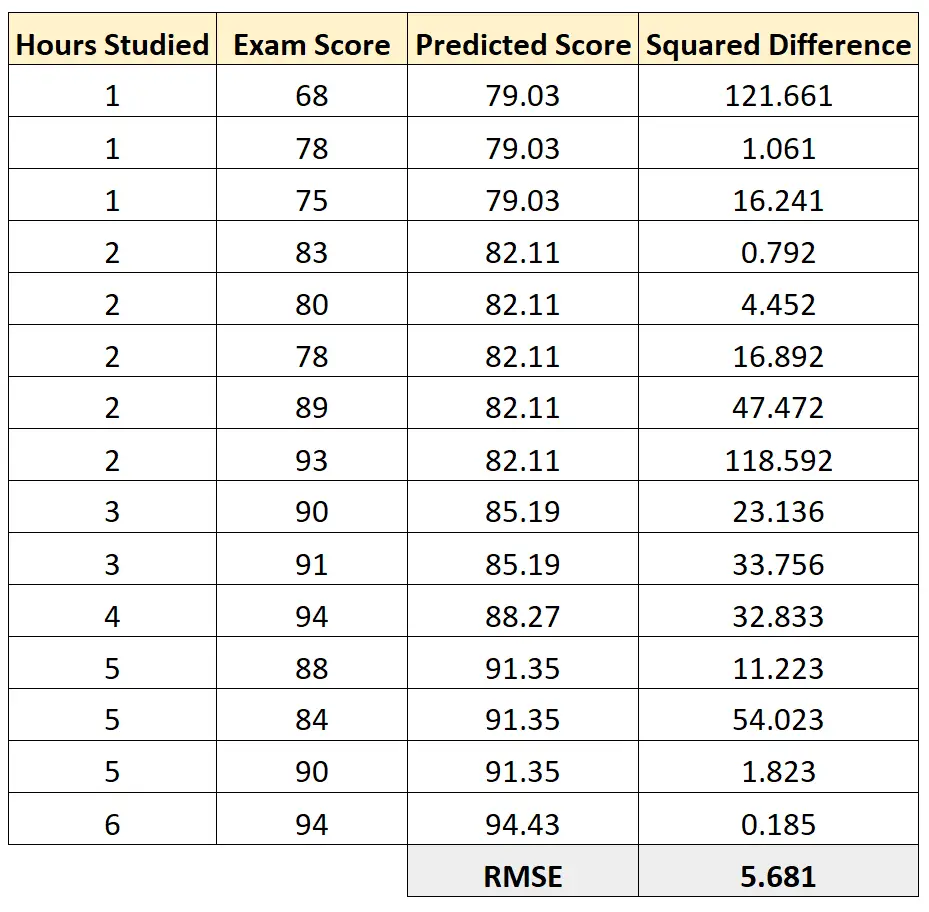
ဤဆုတ်ယုတ်မှုပုံစံ၏ RMSE သည် 5.681 ဖြစ်လာသည်။

ဆုတ်ယုတ်မှုပုံစံတစ်ခု၏ အကြွင်းအကျန်များသည် လေ့လာတွေ့ရှိထားသောဒေတာတန်ဖိုးများနှင့် မော်ဒယ်၏ခန့်မှန်းတန်ဖိုးများကြား ခြားနားချက်များကို သတိရပါ။

လက်ကျန် = (P _i – O _i )

ရွှေ

• P _i သည် dataset ရှိ ^ith observation အတွက် ခန့်မှန်းထားသော တန်ဖိုးဖြစ်သည်။
• O _i သည် dataset အတွင်းရှိ ^ith observation အတွက် သတိပြုမိသောတန်ဖိုးဖြစ်သည်။

ဆုတ်ယုတ်မှုပုံစံတစ်ခု၏ RMSE ကို အောက်ပါအတိုင်း တွက်ချက်ထားကြောင်း သတိရပါ။

RMSE = √ Σ(P _i – O _i ) ² / n

ဆိုလိုသည်မှာ RMSE သည် အကြွင်းအကျန်များ၏ ကွဲလွဲမှု၏ နှစ်ထပ်ကိန်းကို ကိုယ်စားပြုသည်ဟု ဆိုလိုသည်။

ဤသည်မှာ သိထားရန် အသုံးဝင်သော တန်ဖိုးတစ်ခုဖြစ်ပြီး ၎င်းသည် ကျွန်ုပ်တို့အား စောင့်ကြည့်လေ့လာထားသည့် ဒေတာတန်ဖိုးများနှင့် ခန့်မှန်းထားသည့် ဒေတာတန်ဖိုးများကြား ပျမ်းမျှအကွာအဝေးကို အကြံဉာဏ်တစ်ခုပေးသောကြောင့် ဖြစ်သည်။

၎င်းသည် မော်ဒယ်၏ R-squared နှင့် ဆန့်ကျင်ဘက်ဖြစ်ပြီး၊ တုံ့ပြန်မှုကိန်းရှင်တွင် ကွဲလွဲမှု မည်မျှရှိသည်ကို မော်ဒယ်၏ ခန့်မှန်းပေးသူ ကိန်းရှင်(များ) က ရှင်းပြနိုင်သည်။

မတူညီသောမော်ဒယ်များ၏ RMSE တန်ဖိုးများကို နှိုင်းယှဉ်ခြင်း။

RMSE သည် မတူညီသော ဆုတ်ယုတ်မှုပုံစံများ၏ အံအားသင့်မှုကို နှိုင်းယှဉ်ရန်အတွက် အထူးအသုံးဝင်သည်။

ဥပမာအားဖြင့်၊ ကျွန်ုပ်တို့သည် ကျောင်းသားများ၏ စာမေးပွဲရမှတ်များကို ခန့်မှန်းရန် ဆုတ်ယုတ်မှုပုံစံကို တည်ဆောက်လိုသည်ဆိုပါစို့၊ ကျွန်ုပ်တို့သည် ဖြစ်နိုင်ချေရှိသော မော်ဒယ်များစွာတွင် ဖြစ်နိုင်ချေရှိသော အကောင်းဆုံးပုံစံကို ရှာဖွေလိုပါသည်။

ကျွန်ုပ်တို့သည် မတူညီသော ဆုတ်ယုတ်မှုပုံစံသုံးမျိုးနှင့် အံဝင်ခွင်ကျဖြစ်ပြီး ၎င်းတို့၏ သက်ဆိုင်ရာ RMSE တန်ဖိုးများကို ရှာဖွေမည်ဆိုပါစို့။

• မော်ဒယ် 1: 14.5 ၏ RMSE
• မော်ဒယ် 2: 16.7 ၏ RMSE
• မော်ဒယ် 3: 9.8 ၏ RMSE

Model 3 တွင် အနိမ့်ဆုံး RMSE ရှိသည်၊ ၎င်းသည် ဖြစ်နိုင်ချေရှိသော မော်ဒယ်သုံးမျိုးတွင် dataset ကို အကောင်းဆုံး အံဝင်ခွင်ကျဖြစ်စေနိုင်ကြောင်း ကျွန်ုပ်တို့ကိုပြောပြသည်။

ထပ်လောင်းအရင်းအမြစ်များ

RMSE ဂဏန်းတွက်စက်
Excel တွင် RMSE တွက်ချက်နည်း
R ဖြင့် RMSE တွက်နည်း
Python တွင် RMSE တွက်ချက်နည်း