Excel တွင် root mean square error (rmse) ကို တွက်ချက်နည်း
ကိန်းဂဏန်းစာရင်းဇယားများတွင်၊ ဆုတ်ယုတ်မှုခွဲခြမ်းစိတ်ဖြာမှုသည် ကြိုတင်ခန့်မှန်းကိန်းရှင်တစ်ခု၊ x နှင့် တုံ့ပြန်မှုကိန်းရှင် y အကြား ဆက်နွယ်မှုကို နားလည်ရန် ကျွန်ုပ်တို့အသုံးပြုသည့် နည်းလမ်းတစ်ခုဖြစ်သည်။
ကျွန်ုပ်တို့သည် ဆုတ်ယုတ်မှုခွဲခြမ်းစိတ်ဖြာမှုကို လုပ်ဆောင်သောအခါ၊ ခန့်မှန်းသူကိန်းရှင်၏တန်ဖိုးအပေါ်အခြေခံ၍ တုံ့ပြန်မှုကိန်းရှင်၏ ခန့်မှန်းတန်ဖိုးကို ပြောပြသည့် မော်ဒယ်တစ်ခုကို ရရှိပါသည်။
ကျွန်ုပ်တို့၏မော်ဒယ်သည် ပေးထားသောဒေတာအတွဲတစ်ခုနှင့် ကိုက်ညီမှုရှိမရှိကို အကဲဖြတ်ရန် နည်းလမ်းတစ်ခုမှာ ပျမ်းမျှနှစ်ထပ်ကိန်းအမှားကို တွက်ချက်ရန်ဖြစ်ပြီး ကျွန်ုပ်တို့၏ခန့်မှန်းထားသောတန်ဖိုးများသည် ကျွန်ုပ်တို့၏ခန့်မှန်းထားသောတန်ဖိုးများမှ ပျမ်းမျှအားဖြင့် မည်မျှအကွာအဝေးကိုပြသသည့် မက်ထရစ်တစ်ခုဖြစ်သည်။
RMSE ဟုခေါ်သော အများအားဖြင့် ပျမ်းမျှစတုရန်းအမှားကို ရှာဖွေခြင်းအတွက် ဖော်မြူလာမှာ-
RMSE = √[ Σ(P i – O i ) 2 / n ]
ရွှေ-
- ∑ သည် “ပေါင်း” ဟု အဓိပ္ပါယ်ရသော ဖန်စီသင်္ကေတတစ်ခုဖြစ်သည်။
- P i သည် dataset ရှိ ith observation အတွက် ခန့်မှန်းထားသော တန်ဖိုးဖြစ်သည်။
- O i သည် dataset ရှိ ith observation အတွက် သတိပြုမိသောတန်ဖိုးဖြစ်သည်။
- n သည် နမူနာအရွယ်အစားဖြစ်သည်။
နည်းပညာ မှတ်စုများ
- ခန့်မှန်းတန်ဖိုးများကိုထုတ်ပေးသည့် မည်သည့်မော်ဒယ်အမျိုးအစားအတွက်မဆို ပျမ်းမျှစတုရန်းအမှားကို တွက်ချက်နိုင်ပြီး၊ ထို့နောက် ဒေတာအစုတစ်ခု၏ မှတ်သားထားသောတန်ဖိုးများနှင့် နှိုင်းယှဉ်နိုင်သည်။
- Mean square error ကို တစ်ခါတစ်ရံတွင် mean square deviation ဟုခေါ်ပြီး RMSD အဖြစ် အတိုကောက်ခေါ်လေ့ရှိသည်။
ထို့နောက် Excel တွင် mean square error တွက်ချက်နည်း ဥပမာကို ကြည့်ကြပါစို့။
Excel တွင် Mean Square Error တွက်ချက်နည်း
Excel တွင် RMSE တွက်ချက်ရန် built-in function မရှိသော်လည်း၊ ကျွန်ုပ်တို့သည် ၎င်းကိုဖော်မြူလာတစ်ခုတည်းဖြင့် တွက်ချက်နိုင်သည်။ မတူညီသောအခြေအနေနှစ်ခုအတွက် RMSE တွက်ချက်နည်းကို ကျွန်ုပ်တို့ပြသပါမည်။
ဇာတ်လမ်း ၁
အခြေအနေတစ်ခုတွင်၊ သင့်မော်ဒယ်မှ ခန့်မှန်းထားသော တန်ဖိုးများပါဝင်သော ကော်လံတစ်ခုနှင့် လေ့လာတွေ့ရှိထားသည့် တန်ဖိုးများပါဝင်သော အခြားကော်လံတစ်ခု ရှိနိုင်ပါသည်။ အောက်ဖော်ပြပါပုံသည် ဤအခြေအနေ၏ ဥပမာကို ပြသည်-
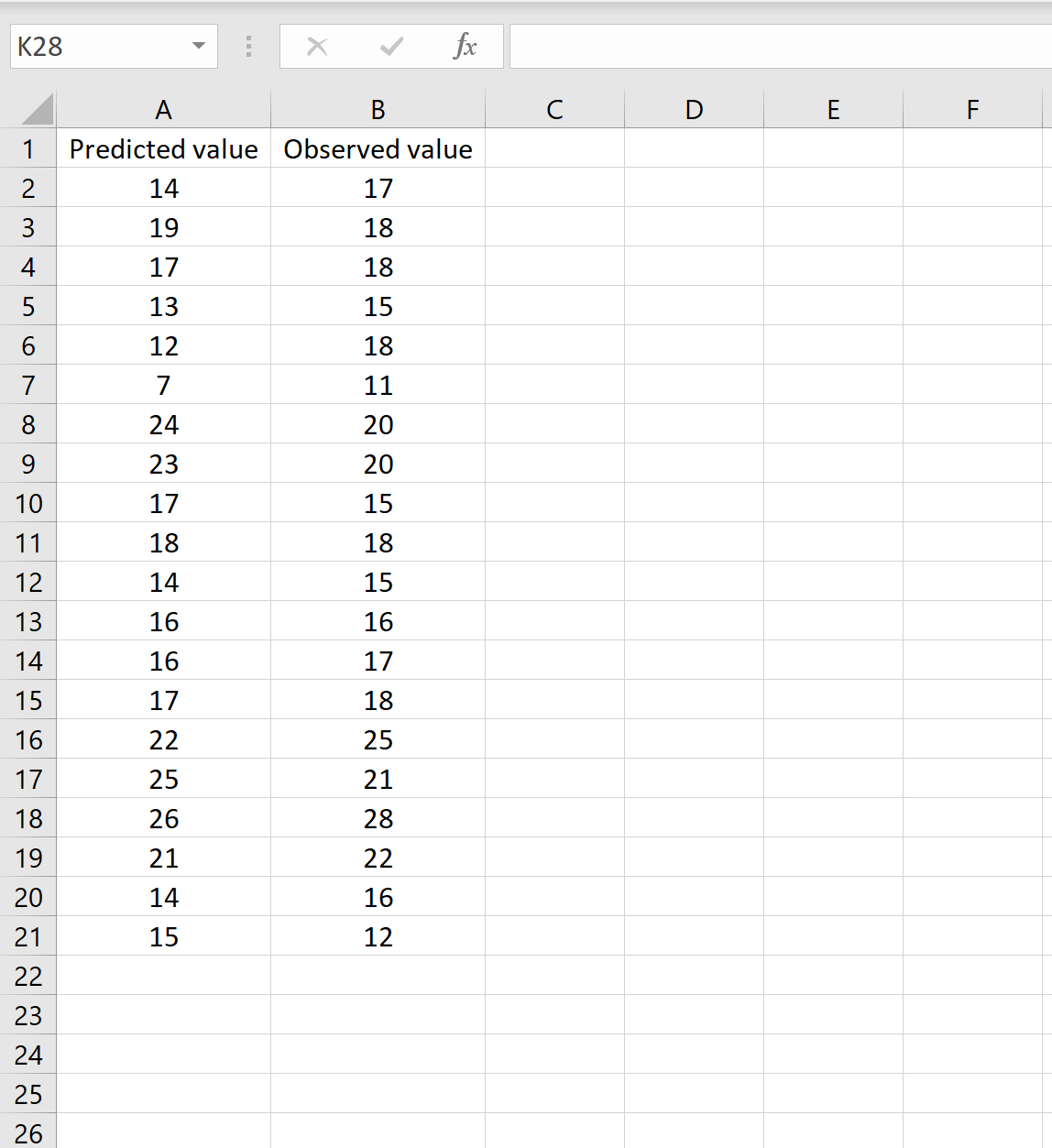
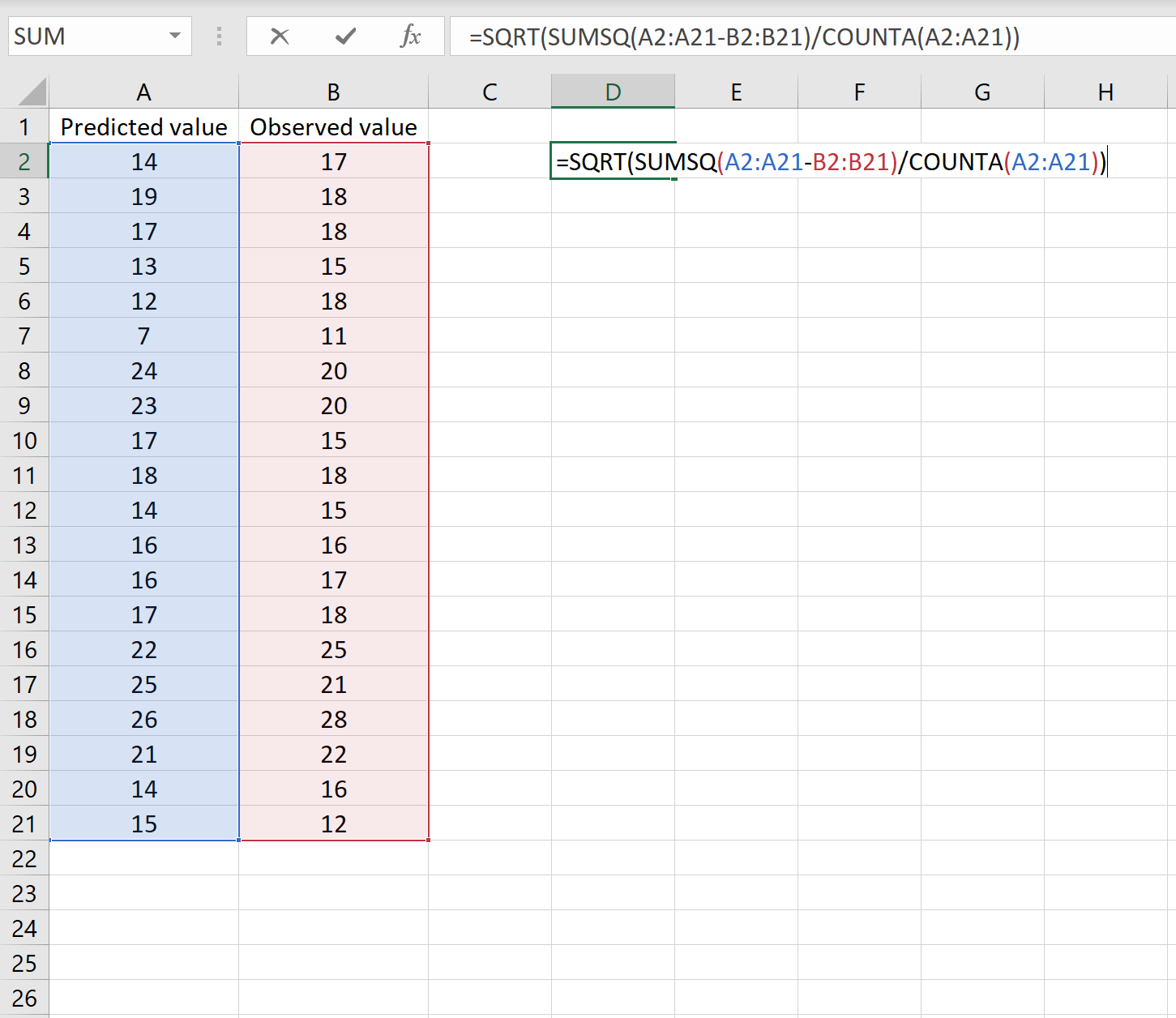
သို့ဆိုလျှင်၊ သင်သည် မည်သည့်ဆဲလ်တွင်မဆို အောက်ပါဖော်မြူလာကို ရိုက်ထည့်ပြီး CTRL+SHIFT+ENTER ကိုနှိပ်ခြင်းဖြင့် RMSE ကို တွက်ချက်နိုင်သည်-
=SQRT(SUMSQ(A2:A21-B2:B21) / COUNT(A2:A21))
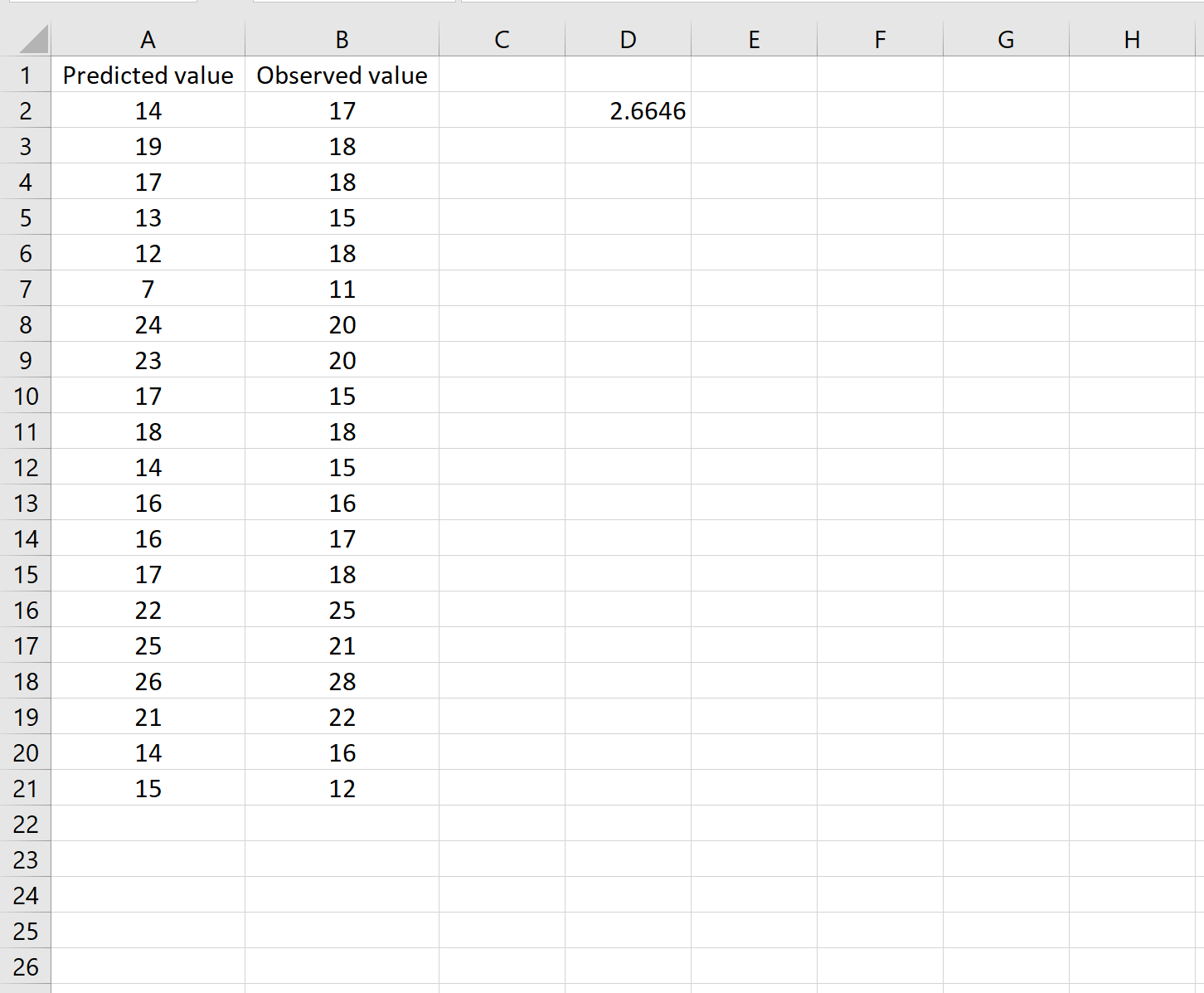
၎င်းသည် ပျမ်းမျှစတုရန်းအမှားသည် 2.6646 ဖြစ်ကြောင်း ကျွန်ုပ်တို့ကိုပြောပြသည်။
ဖော်မြူလာသည် အနည်းငယ် ဆန်းကျယ်ပုံရသော်လည်း ၎င်းကို ဖြိုခွဲလိုက်သည်နှင့် အဓိပ္ပါယ်ရှိလာသည်-
= SQRT( SUMSQ(A2:A21-B2:B21) / COUNT(A2:A21) )
- ဦးစွာ၊ ကျွန်ုပ်တို့သည် SUMSQ() လုပ်ဆောင်ချက်ကို အသုံးပြု၍ ခန့်မှန်းထားသော နှင့် လေ့လာတွေ့ရှိထားသော တန်ဖိုးများအကြား ကွာခြားချက်များ၏ လေးထောင့်ကိန်းများကို တွက်ချက်ပါသည်။
- ထို့နောက်၊ ကျွန်ုပ်တို့သည် အလွတ်မဟုတ်သော အပိုင်းအခြားရှိ ဆဲလ်အရေအတွက်ကို ရေတွက်သည့် COUNTA() ကို အသုံးပြု၍ ဒေတာအတွဲ၏နမူနာအရွယ်အစားဖြင့် ပိုင်းခြားပါသည်။
- နောက်ဆုံးအနေနဲ့၊ SQRT() လုပ်ဆောင်ချက်ကို အသုံးပြုပြီး တွက်ချက်မှုတစ်ခုလုံးရဲ့ နှစ်ထပ်ကိန်းကို ယူပါတယ်။
ဇာတ်လမ်း ၂
အခြားအခြေအနေတွင်၊ သင်သည် ခန့်မှန်းထားသော နှင့် စောင့်ကြည့်ထားသော တန်ဖိုးများကြား ခြားနားချက်များကို တွက်ချက်ပြီးဖြစ်သည်။ ဤကိစ္စတွင် သင်သည် ကွဲပြားမှုများကိုပြသသော ကော်လံတစ်ခုသာရှိသည်။
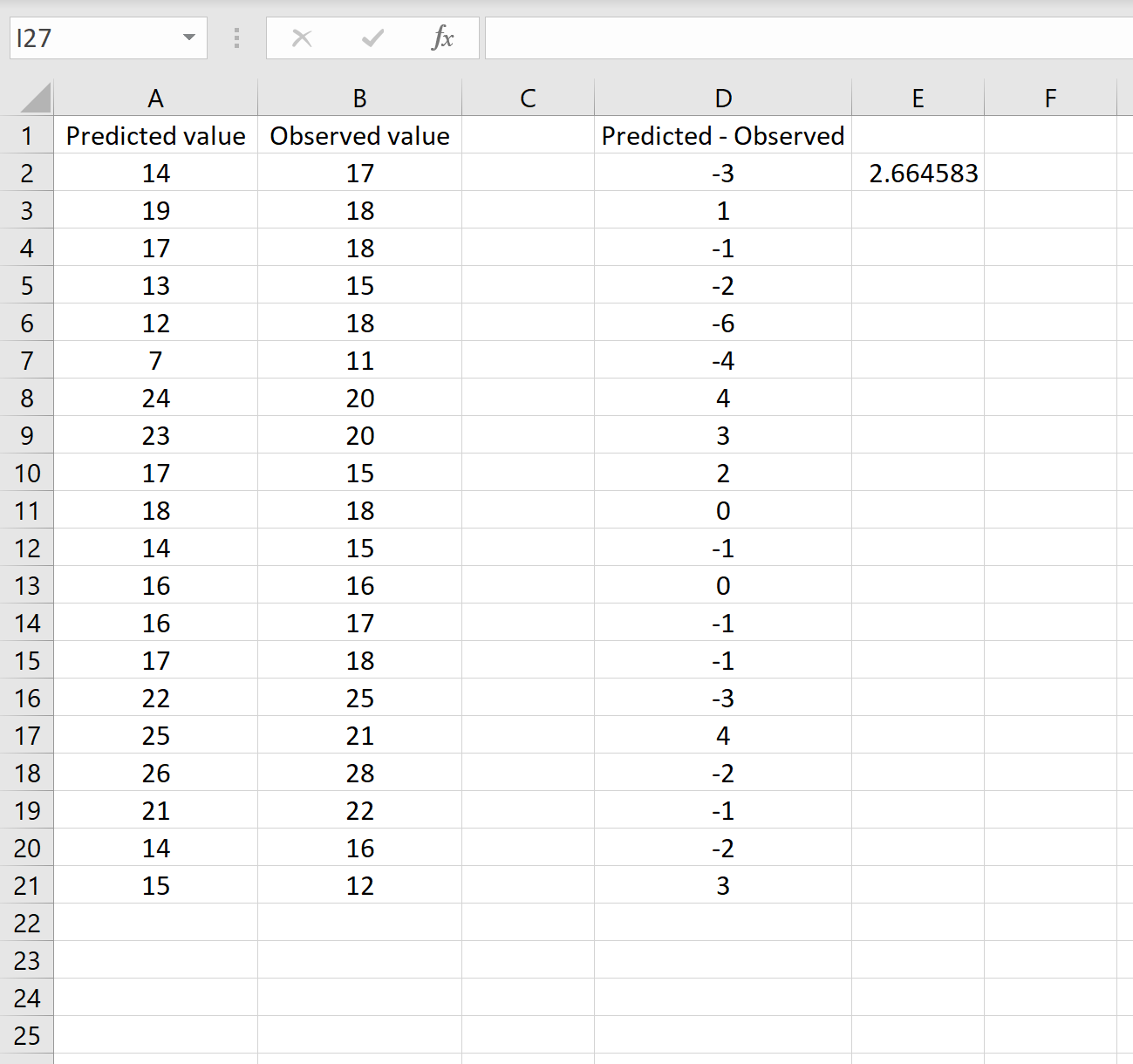
အောက်ဖော်ပြပါပုံသည် ဤအခြေအနေ၏ဥပမာတစ်ခုပြသထားသည်။ ခန့်မှန်းထားသောတန်ဖိုးများကို ကော်လံ A တွင်ပြသသည်၊၊ ကော်လံ B တွင်လေ့လာထားသောတန်ဖိုးများနှင့် ကော်လံ D တွင် ခန့်မှန်းထားသည့်တန်ဖိုးများနှင့် ခြားနားချက်-
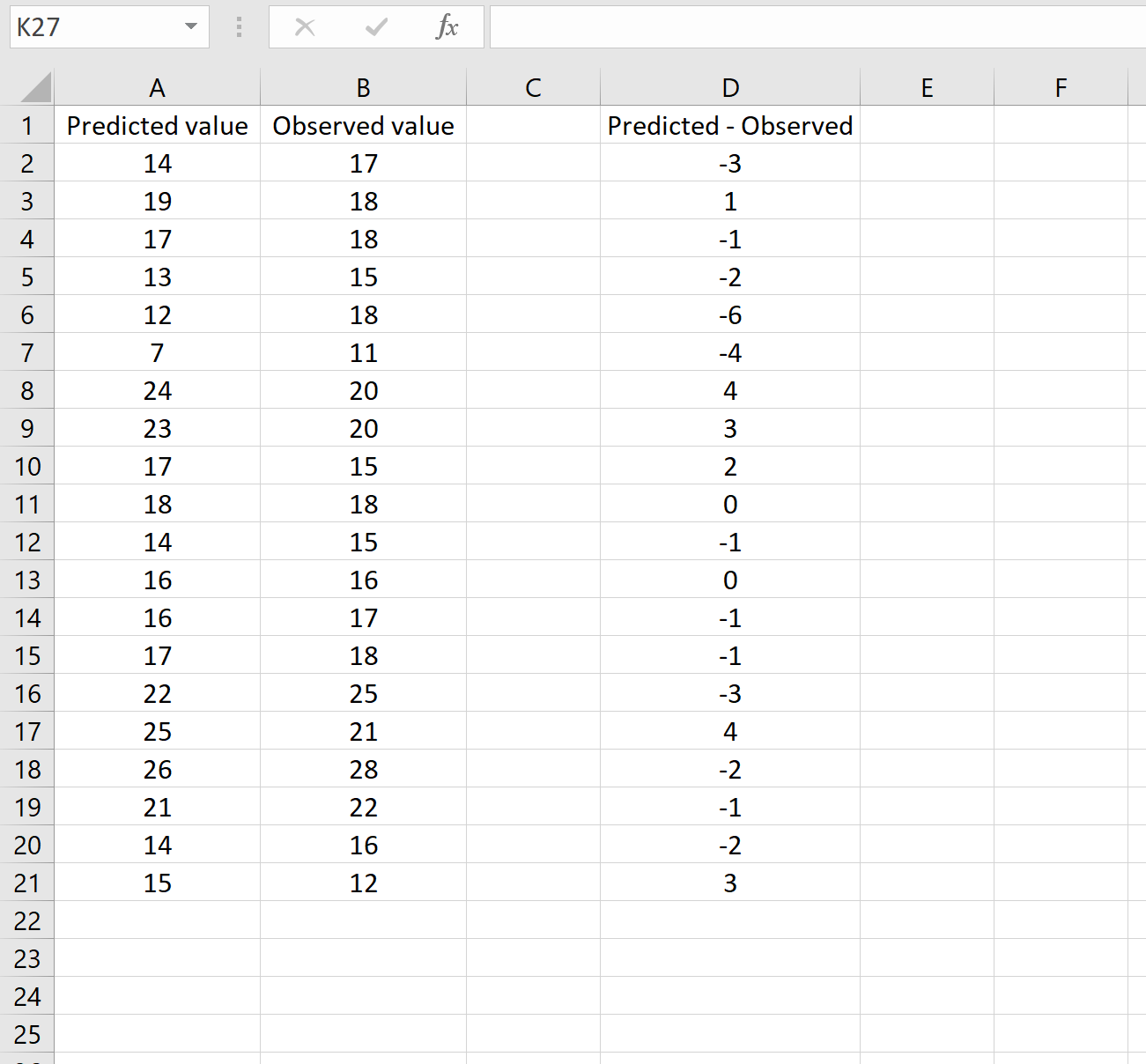
သို့ဆိုလျှင်၊ သင်သည် မည်သည့်ဆဲလ်တွင်မဆို အောက်ပါဖော်မြူလာကို ရိုက်ထည့်ပြီး CTRL+SHIFT+ENTER ကိုနှိပ်ခြင်းဖြင့် RMSE ကို တွက်ချက်နိုင်သည်-
=SQRT(SUMSQ(D2:D21) / COUNT(D2:D21))
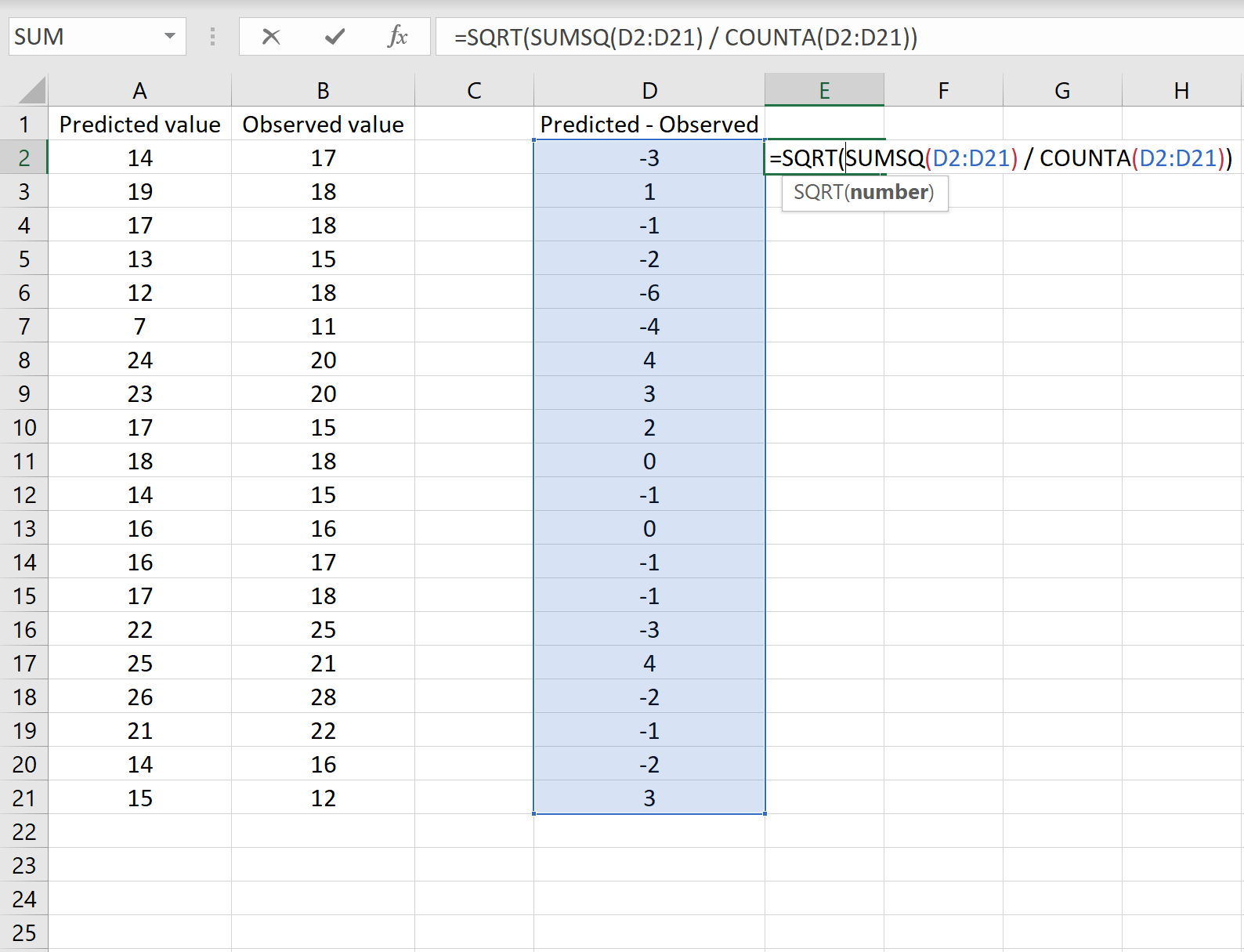
၎င်းသည် ပျမ်းမျှစတုရန်းအမှားသည် 2.6646 ဖြစ်သည်၊ ၎င်းသည် ပထမအခြေအနေတွင်ရရှိသောရလဒ်နှင့် ကိုက်ညီသည်ဟု ကျွန်ုပ်တို့ကိုပြောပြသည်။ RMSE တွက်ချက်ရာတွင် ဤနည်းလမ်းနှစ်ခုသည် တူညီကြောင်း အတည်ပြုပါသည်။
ဤအခြေအနေတွင် ကျွန်ုပ်တို့အသုံးပြုခဲ့သော ဖော်မြူလာသည် ယခင်အခြေအနေတွင် ကျွန်ုပ်တို့အသုံးပြုခဲ့သည့်အရာနှင့် အနည်းငယ်သာ ကွာခြားပါသည်-
= SQRT( SUMSQ(D2:D21) / COUNT(D2:D21) )
- ကော်လံ D တွင် ခန့်မှန်းထားသော နှင့် စောင့်ကြည့်ထားသော တန်ဖိုးများကြား ခြားနားချက်များကို ကျွန်ုပ်တို့ တွက်ချက်ထားပြီးဖြစ်သောကြောင့်၊ SUMSQ() လုပ်ဆောင်ချက်ကို အသုံးပြု၍ နှစ်ထပ်ကိန်းကွဲမှုများ၏ ပေါင်းလဒ်ကို တွက်ချက်နိုင်ပါသည် ။ ကော်လံ D မှတန်ဖိုးများကိုသာလုပ်ဆောင်သည်။
- ထို့နောက်၊ ကျွန်ုပ်တို့သည် အလွတ်မဟုတ်သော အပိုင်းအခြားရှိ ဆဲလ်အရေအတွက်ကို ရေတွက်သည့် COUNTA() ကို အသုံးပြု၍ ဒေတာအတွဲ၏နမူနာအရွယ်အစားဖြင့် ပိုင်းခြားပါသည် ။
- နောက်ဆုံးအနေနဲ့၊ SQRT() လုပ်ဆောင်ချက်ကို အသုံးပြုပြီး တွက်ချက်မှုတစ်ခုလုံးရဲ့ နှစ်ထပ်ကိန်းကို ယူပါတယ် ။
RMSE ကို ဘယ်လိုအဓိပ္ပာယ်ဖွင့်မလဲ။
အစောပိုင်းတွင် ဖော်ပြခဲ့သည့်အတိုင်း RMSE သည် ဆုတ်ယုတ်မှုပုံစံ (သို့မဟုတ် ခန့်မှန်းတန်ဖိုးများကို ထုတ်လုပ်သည့် မော်ဒယ်) သည် ဒေတာအစုတစ်ခုအား မည်မျှ အံဝင်ခွင်ကျဖြစ်စေနိုင်သည်ကို ကြည့်ရန် အသုံးဝင်သောနည်းလမ်းတစ်ခုဖြစ်သည်။
RMSE ကြီးလေလေ၊ ခန့်မှန်းထားသည့်နှင့် စောင့်ကြည့်ထားသော တန်ဖိုးများအကြား ကွာခြားလေလေ၊ ဆုတ်ယုတ်မှုပုံစံသည် ဒေတာနှင့် ကိုက်ညီလေလေဟု ဆိုလိုသည်။ အပြန်အလှန်အားဖြင့်၊ RMSE သေးငယ်လေ၊ မော်ဒယ်သည် ဒေတာကို အံဝင်ခွင်ကျဖြစ်စေနိုင်လေဖြစ်သည်။
ဒေတာနှင့်အကိုက်ညီဆုံးမော်ဒယ်နှစ်ခု၏ RMSE ကိုနှိုင်းယှဉ်ရန် အထူးအသုံးဝင်ပါသည်။
Excel တွင် နောက်ထပ် သင်ခန်းစာများအတွက်၊ စာရင်းဇယားများဆိုင်ရာ Excel သင်ခန်းစာများအားလုံးကို စာရင်းပြုစုထားသည့် ကျွန်ုပ်တို့၏ Excel Guides စာမျက်နှာကို စစ်ဆေးကြည့်ပါ။