Sas တွင် အရေအတွက် ဆုတ်ယုတ်မှုအား မည်သို့လုပ်ဆောင်ရမည်နည်း

Linear regression သည် တစ်ခု သို့မဟုတ် တစ်ခုထက်ပိုသော ကြိုတင်ခန့်မှန်းကိန်းရှင်များနှင့် တုံ့ပြန်မှုကိန်းရှင် အကြား ဆက်နွယ်မှုကို နားလည်ရန် ကျွန်ုပ်တို့ အသုံးပြုနိုင်သည့် နည်းလမ်းတစ်ခုဖြစ်သည်။

ပုံမှန်အားဖြင့်၊ ကျွန်ုပ်တို့သည် linear regression လုပ်ဆောင်သောအခါ၊ တုံ့ပြန်မှုကိန်းရှင်၏ ပျမ်းမျှတန်ဖိုးကို ခန့်မှန်းလိုပါသည်။

သို့သော်၊ ကျွန်ုပ်တို့သည် တုံ့ပြန်မှုတန်ဖိုး၏ ရာခိုင်နှုန်း တန်ဖိုး၊ 30th ရာခိုင်နှုန်း၊ 90th ရာခိုင်နှုန်း၊ 98th ရာခိုင်နှုန်းစသည်ဖြင့် ခန့်မှန်းရန် quantile regression ဟုခေါ်သော နည်းလမ်းကို အသုံးပြုနိုင်သည်။

SAS တွင် quantile regression လုပ်ဆောင်ရန်၊ proc quantreg statement ကို သုံးနိုင်သည်။

အောက်ဖော်ပြပါ ဥပမာသည် လက်တွေ့တွင် SAS တွင် ပမာဏဆုတ်ယုတ်မှုကို မည်သို့လုပ်ဆောင်ရမည်ကို ပြသထားသည်။

ဥပမာ- SAS တွင် Quantile Regression လုပ်ဆောင်ခြင်း။

ကျွန်ုပ်တို့တွင် အတန်းတစ်တန်းရှိ ကျောင်းသားများအတွက် စာမေးပွဲရမှတ်နှင့် သင်ကြားသည့် နာရီအရေအတွက်နှင့် သက်ဆိုင်သော စာမေးပွဲရမှတ်ကို ပြသသော SAS တွင် အောက်ပါဒေတာအစုံရှိသည်ဆိုပါစို့။

 /*create dataset*/
data original_data;
    input hours score;
    datalines ;
1 75
1 79
2 78
2 83
2 85
3 84
3 84
3 89
4 93
4 88
4 79
4 94
5 96
5 98
;
run ;

/*view dataset*/
proc print data = original_data;

ဆက်လက်၍၊ ကျွန်ုပ်တို့သည် ကြိုတင်ခန့်မှန်းကိန်းရှင်ကိန်းရှင်နှင့် တုံ့ပြန်မှုကိန်းရှင်အဖြစ် စာမေးပွဲရမှတ်များအဖြစ် လေ့လာထားသော နာရီများကို အသုံးပြု၍ အရေအတွက် ဆုတ်ယုတ်မှုပုံစံကို ဖြည့်သွင်းပါမည်။

လေ့လာခဲ့သည့် နာရီအရေအတွက်ပေါ်မူတည်၍ မျှော်မှန်းထားသည့် 90th ရာခိုင်နှုန်း စာမေးပွဲရမှတ်များကို ခန့်မှန်းရန် မော်ဒယ်ကို အသုံးပြုပါမည်။

 /*perform quantile regression*/
proc quantreg data =original_data;
    model score = hours / quantile = 0.9 ;
run ;

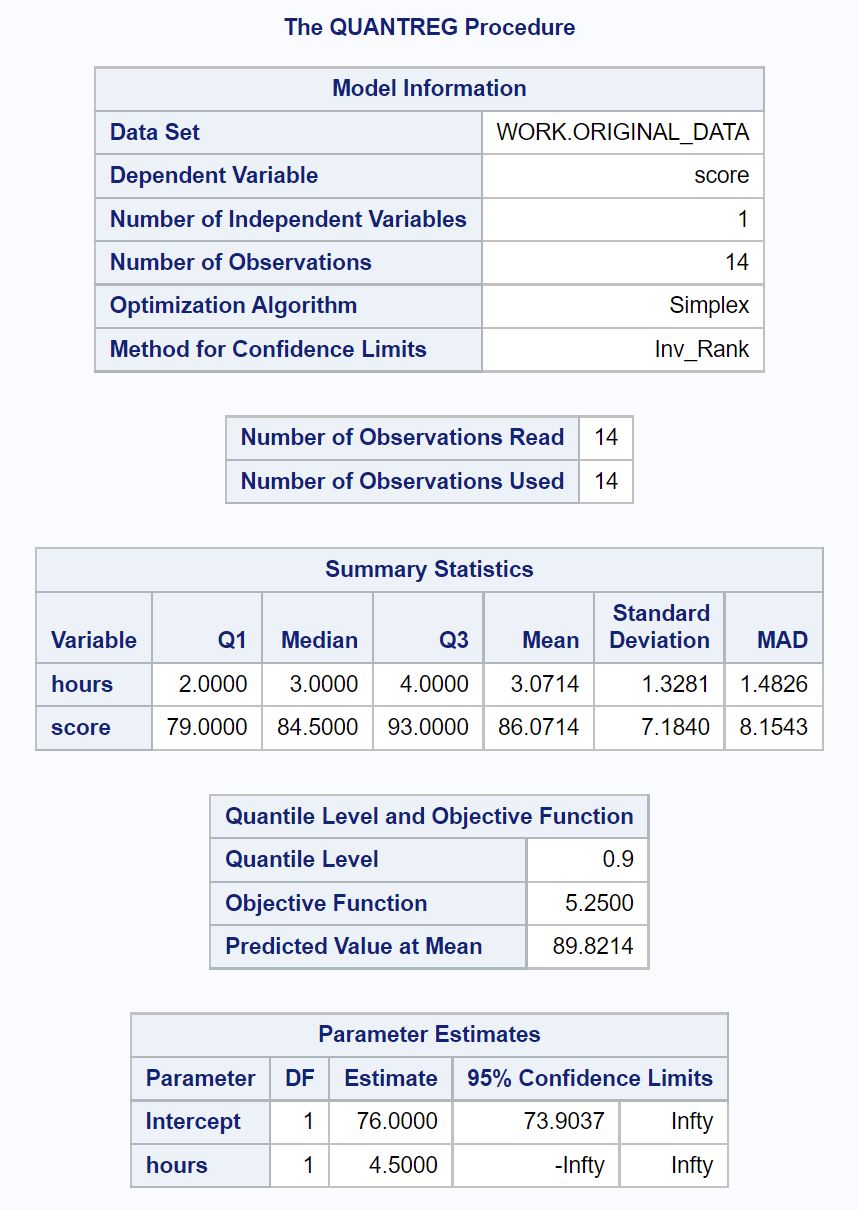
ရလဒ်မှ ခန့်မှန်းခြေ ဆုတ်ယုတ်မှုညီမျှခြင်းကို ကျွန်ုပ်တို့ မြင်နိုင်သည်-

အကြိမ် ၉၀ မြောက် ရာခိုင်နှုန်း စာမေးပွဲ ရမှတ် = ၇၆ + ၄.၅ (နာရီ)

ဥပမာအားဖြင့်၊ 2 နာရီစာလေ့လာသောကျောင်းသားအားလုံး၏ 90th ရာခိုင်နှုန်းရမှတ်သည် 85 ဖြစ်သင့်သည်-

90th ရာခိုင်နှုန်း စာမေးပွဲရမှတ် = 76 + 4.5*(2) = 85 ။

အထွက်သည် ကွက်ကွက်ပေါ်တွင် တပ်ဆင်ထားသော ဆုတ်ယုတ်မှုမျဉ်းနှင့်အတူ ဒေတာအကြမ်း၏ အပိုင်းအစကို ပြသသည်-

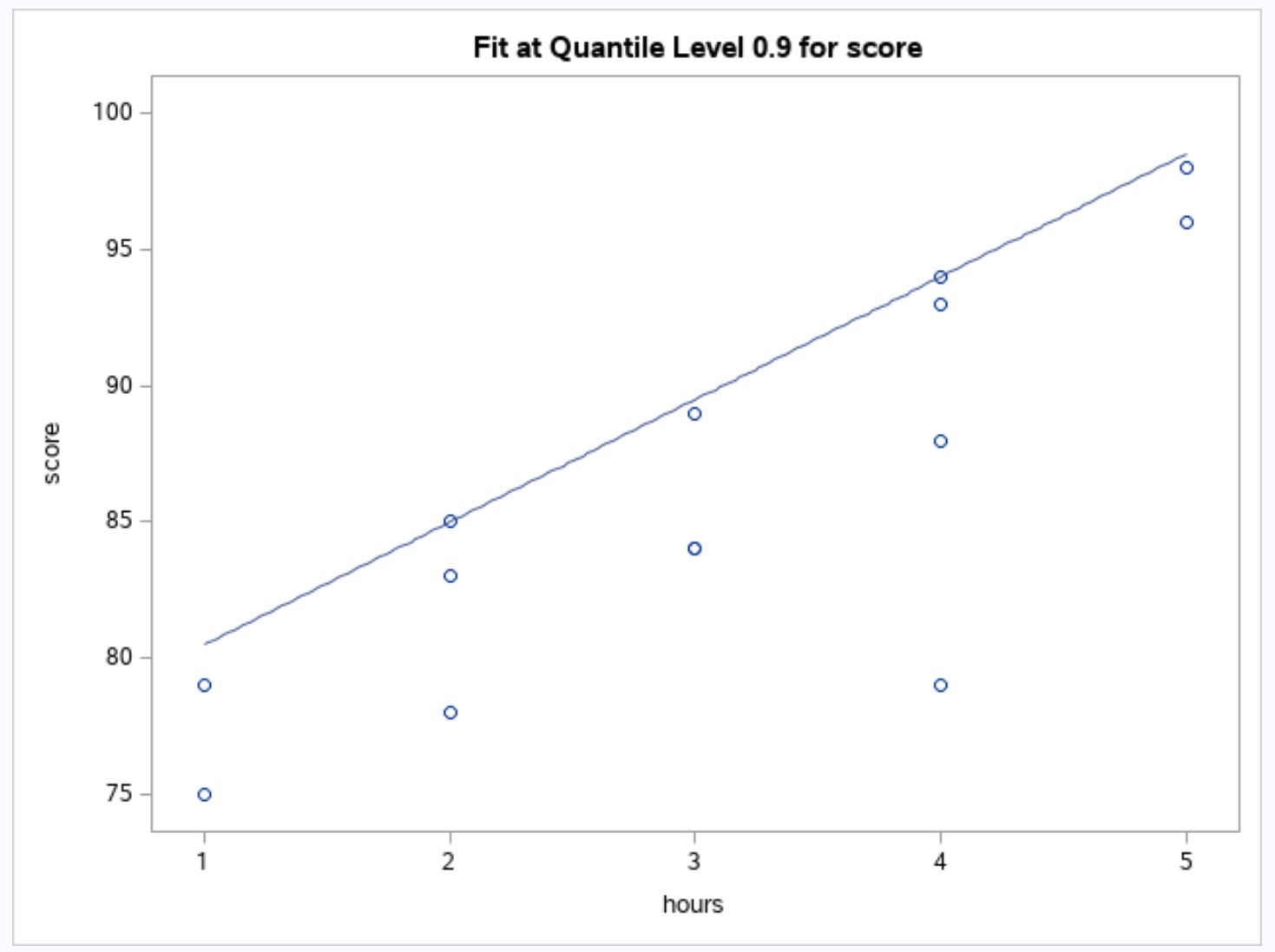
သမားရိုးကျ ဆုတ်ယုတ်မှုပုံစံနှင့်မတူဘဲ၊ ဤဆုတ်ယုတ်မှုပုံစံတွင် တပ်ဆင်ထားသော လိုင်းသည် ခန့်မှန်းသူကိန်းရှင်၏ တန်ဖိုးတစ်ခုစီ၏ 90th ရာခိုင်နှုန်းကို ပျမ်းမျှတန်ဖိုးအစား ဖြတ်သန်းသွားပါသည်။

ထပ်လောင်းအရင်းအမြစ်များ

အောက်ဖော်ပြပါ သင်ခန်းစာများသည် R တွင် အခြားဘုံအလုပ်များကို မည်သို့လုပ်ဆောင်ရမည်ကို ရှင်းပြသည်-

R တွင် ရိုးရှင်းသော linear regression လုပ်နည်း
R တွင် linear regression အများအပြားလုပ်ဆောင်နည်း
R တွင် quadratic regression ကို မည်သို့လုပ်ဆောင်ရမည်နည်း။