Sas တွင် မျဉ်းကြောင်းပြန်ဆုတ်ခြင်းများစွာကို မည်သို့လုပ်ဆောင်ရမည်နည်း။

Multiple linear regression သည် ကြိုတင်ခန့်မှန်းကိန်းရှင် နှစ်ခု သို့မဟုတ် ထို့ထက်ပိုသော ကိန်းရှင်များနှင့် တုံ့ပြန်မှုကိန်းရှင် တစ်ခုကြား ဆက်နွယ်မှုကို နားလည်ရန် ကျွန်ုပ်တို့ အသုံးပြုနိုင်သည့် နည်းလမ်းတစ်ခုဖြစ်သည်။

ဤသင်ခန်းစာသည် SAS တွင် မျဉ်းကြောင်းပြန်ဆုတ်ခြင်းကို မည်သို့လုပ်ဆောင်ရမည်ကို ရှင်းပြထားသည်။

အဆင့် 1: ဒေတာကိုဖန်တီးပါ။

ကျောင်းသားများ၏ နောက်ဆုံးစာမေးပွဲအဆင့်ကို ခန့်မှန်းရန် စာကျက်ချိန်နာရီအရေအတွက်နှင့် လက်တွေ့စာမေးပွဲအရေအတွက်တို့ကို အသုံးပြုသည့် Multiple linear regression model နှင့် ကိုက်ညီလိုသည်ဆိုပါစို့။

စာမေးပွဲရမှတ် = β ₀ + β ₁ (နာရီ) + β ₂ (အကြိုစာမေးပွဲများ)

ပထမဦးစွာ၊ ကျောင်းသား 20 အတွက် ဤအချက်အလက်ပါရှိသော ဒေတာအတွဲကို ဖန်တီးရန် အောက်ပါကုဒ်ကို အသုံးပြုပါမည်။

 /*create dataset*/
data exam_data;
    input hours prep_exams score;
    datalines ;
1 1 76
2 3 78
2 3 85
4 5 88
2 2 72
1 2 69
5 1 94
4 1 94
2 0 88
4 3 92
4 4 90
3 3 75
6 2 96
5 4 90
3 4 82
4 4 85
6 5 99
2 1 83
1 0 62
2 1 76
;
run ;

အဆင့် 2- Multiple Linear Regression ကို လုပ်ဆောင်ပါ။

ထို့နောက်၊ ဒေတာနှင့် များစွာသော linear regression model ကို ကိုက်ညီရန် proc reg ကို အသုံးပြုပါမည်။

 /*fit multiple linear regression model*/
proc reg data =exam_data;
    model score = hours prep_exams;
run ; 

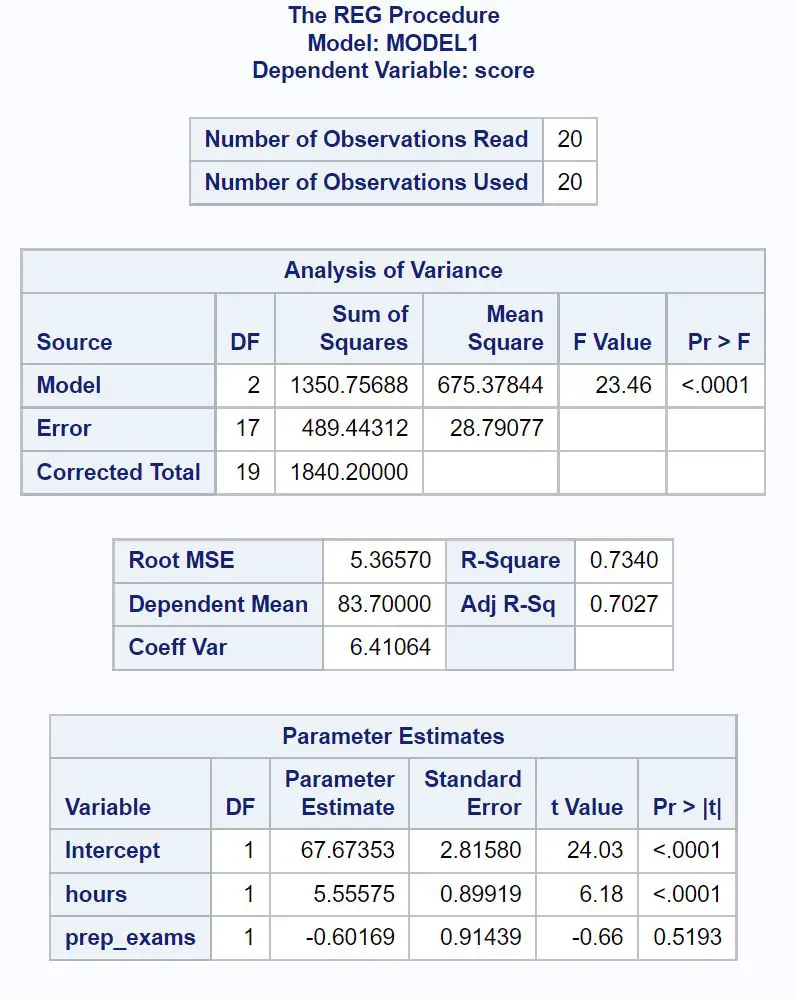
ဇယားတစ်ခုစီရှိ အကိုက်ညီဆုံးနံပါတ်များကို မည်သို့အဓိပ္ပာယ်ဖွင့်ဆိုရမည်ကို ဤတွင် ဖော်ပြပါရှိသည်။

ကွာဟချက် ခွဲခြမ်းစိတ်ဖြာမှုဇယား-

ဆုတ်ယုတ်မှုမော်ဒယ်၏ စုစုပေါင်း F-တန်ဖိုး သည် 23.46 ဖြစ်ပြီး သက်ဆိုင်ရာ p-တန်ဖိုးမှာ <0.0001 ဖြစ်သည်။

ဤ p-value သည် 0.05 ထက်နည်းသောကြောင့်၊ regression model တစ်ခုလုံးသည် စာရင်းအင်းအရ သိသာထင်ရှားသည်ဟု ကျွန်ုပ်တို့ကောက်ချက်ချပါသည်။

မော်ဒယ်အံစာစားပွဲ

R-Square တန်ဖိုးသည် ဖြေဆိုထားသည့် နာရီအရေအတွက်နှင့် ကြိုတင်ပြင်ဆင်သည့် စာမေးပွဲအရေအတွက်အလိုက် ရှင်းပြနိုင်သည့် စာမေးပွဲရမှတ်များတွင် ကွဲလွဲမှုရာခိုင်နှုန်းကို ပြောပြသည်။

ယေဘူယျအားဖြင့်၊ ဆုတ်ယုတ်မှုပုံစံတစ်ခု၏ R-squared တန်ဖိုး ပိုကြီးလေ၊ ခန့်မှန်းသူကိန်းရှင်များသည် တုံ့ပြန်မှုကိန်းရှင်၏တန်ဖိုးကို ခန့်မှန်းရာတွင် ပိုကောင်းလေဖြစ်သည်။

ဤကိစ္စတွင်၊ စာမေးပွဲရမှတ်များ ကွဲလွဲမှု၏ 73.4% ကို လေ့လာသည့် နာရီအရေအတွက်နှင့် ကြိုတင်ပြင်ဆင်ထားသော စာမေးပွဲအရေအတွက်ဖြင့် ရှင်းပြနိုင်သည်။

Root MSE တန်ဖိုးကိုလည်း သိဖို့ အသုံးဝင်ပါတယ်။ ၎င်းသည် သတိပြုမိသော တန်ဖိုးများနှင့် ဆုတ်ယုတ်မှုမျဉ်းကြား ပျမ်းမျှအကွာအဝေးကို ကိုယ်စားပြုသည်။

ဤဆုတ်ယုတ်မှုပုံစံတွင်၊ လေ့လာတွေ့ရှိထားသောတန်ဖိုးများသည် ဆုတ်ယုတ်မှုမျဉ်းမှ ပျမ်းမျှယူနစ် 5.3657 ဖြင့် သွေဖည်သွားပါသည်။

ကန့်သတ်ချက် ခန့်မှန်းချက်ဇယား-

တပ်ဆင်ထားသော regression equation ကိုရေးရန် ဤဇယားရှိ parameter ခန့်မှန်းတန်ဖိုးများကို အသုံးပြုနိုင်သည်။

စာမေးပွဲရမှတ် = 67.674 + 5.556*(နာရီ) – 0.602*(prep_exams)

လေ့လာမှုနာရီအရေအတွက်နှင့် ၎င်းတို့ဖြေဆိုခဲ့သော လက်တွေ့စာမေးပွဲအရေအတွက်အပေါ် အခြေခံ၍ ကျောင်းသားတစ်ဦး၏ ခန့်မှန်းခြေ စာမေးပွဲရမှတ်ကို ရှာဖွေရန် ဤညီမျှခြင်းအား ကျွန်ုပ်တို့ အသုံးပြုနိုင်ပါသည်။

ဥပမာအားဖြင့်၊ ၃ နာရီစာလေ့လာပြီး ကြိုတင်ပြင်ဆင်စာမေးပွဲ ၂ ကြိမ်ဖြေဆိုသော ကျောင်းသားသည် စာမေးပွဲရမှတ် 83.1 ရရှိသင့်သည်-

ခန့်မှန်းခြေ စာမေးပွဲရမှတ် = 67.674 + 5.556*(3) – 0.602*(2) = 83.1

နာရီများအတွက် p-တန်ဖိုး (<0.0001) သည် 0.05 ထက်နည်းသည်၊ ဆိုလိုသည်မှာ ၎င်းသည် စာမေးပွဲရလဒ်နှင့် စာရင်းအင်းအရ သိသာထင်ရှားသော ဆက်စပ်မှုရှိသည်။

သို့သော်၊ ကြိုတင်ပြင်ဆင်မှုစာမေးပွဲများအတွက် p-တန်ဖိုး (0.5193) သည် 0.05 ထက်မနည်းပါ၊ ဆိုလိုသည်မှာ ၎င်းတွင် စာမေးပွဲရလဒ်နှင့် စာရင်းအင်းအရ သိသာထင်ရှားသော ဆက်စပ်မှုမရှိပါ။

၎င်းတို့သည် စာရင်းအင်းအရ သိသာထင်ရှားခြင်းမရှိသောကြောင့် ကြိုတင်ပြင်ဆင်မှုစာမေးပွဲများကို မော်ဒယ်မှဖယ်ရှားရန် ဆုံးဖြတ်နိုင်ပြီး ယင်းအစား ရိုးရှင်းသောမျဉ်းကြောင်းဆုတ်ယုတ်မှုအား တစ်ခုတည်းသော ခန့်မှန်းချက်ကိန်းရှင်အဖြစ် လေ့လာထားသော နာရီများကို အသုံးပြု၍ လုပ်ဆောင်နိုင်ပါသည်။

ထပ်လောင်းအရင်းအမြစ်များ

အောက်ဖော်ပြပါ သင်ခန်းစာများသည် SAS တွင် အခြားဘုံအလုပ်များကို မည်သို့လုပ်ဆောင်ရမည်ကို ရှင်းပြသည်-

SAS တွင် ဆက်စပ်မှုကို တွက်ချက်နည်း
SAS တွင် ရိုးရှင်းသော linear regression လုပ်ဆောင်နည်း
SAS တွင် one-way ANOVA လုပ်ဆောင်နည်း