Sas တွင် odds ratio တွက်ချက်နည်း (နမူနာဖြင့်)

စာရင်းဇယားများတွင်၊ odds ratio သည် ကုသမှုအုပ်စုတစ်ခုတွင် ဖြစ်ပျက်နေသော အဖြစ်အပျက်တစ်ခု၏ မသာမယာအချိုးအစားကို ထိန်းချုပ်သည့်အုပ်စုတွင် ဖြစ်ပျက်နေသည့် အဖြစ်အပျက်တစ်ခု၏ မသာမယာများနှင့် အချိုးကို ပြောပြသည်။

အောက်ပါဖော်မတ်ကိုယူသည့် ဇယား 2 နှင့် 2 တွင် ခွဲခြမ်းစိတ်ဖြာမှုလုပ်ဆောင်သည့်အခါ အချိုးမညီမှုအချိုးကို ကျွန်ုပ်တို့ တွက်ချက်လေ့ရှိသည်-

SAS တွင် ထူးထူးခြားခြား အချိုးတစ်ခုကို တွက်ချက်ရန်၊ ကျွန်ုပ်တို့သည် PROC FREQ ထုတ်ပြန်ချက်ကို အသုံးပြုနိုင်ပါသည်။

အောက်ဖော်ပြပါ ဥပမာသည် ဤဖော်ပြချက်ကို လက်တွေ့တွင် မည်သို့အသုံးပြုရမည်ကို ပြသထားသည်။

ဥပမာ- SAS တွင် ထူးထူးခြားခြား အချိုးတစ်ခုကို တွက်ချက်ခြင်း။

ဘတ်စကတ်ဘောကစားသမား ၅၀ သည် လေ့ကျင့်ရေးအစီအစဉ်အသစ်ကို အသုံးပြုနေပြီး ကစားသမား ၅၀ သည် လေ့ကျင့်ရေးအစီအစဉ်ဟောင်းကို အသုံးပြုနေသည်ဆိုပါစို့။ ပရိုဂရမ်၏အဆုံးတွင်၊ ကစားသမားတစ်ဦးစီသည် ကျွမ်းကျင်မှုစမ်းသပ်မှုတစ်ခုကို ဖြေဆိုအောင်မြင်ကြောင်း သိရှိရန် ကျွန်ုပ်တို့ စမ်းသပ်သည်။

အောက်ပါဇယားတွင် ၎င်းတို့အသုံးပြုခဲ့သည့် ပရိုဂရမ်အပေါ်အခြေခံ၍ အောင်မြင်ပြီး ကျရှုံးခဲ့သော ကစားသမားအရေအတွက်ကို ပြသသည်-

ပရိုဂရမ်အသစ်ကို အသုံးပြု၍ ပရိုဂရမ်ဟောင်းကို အသုံးပြု၍ ပရိုဂရမ်ဟောင်းကို အသုံးပြု၍ ကစားသမားတစ်ဦး၏ အရည်အချင်းစစ်စာမေးပွဲကို အောင်မြင်နိုင်ခြေကို နှိုင်းယှဉ်ရန် အလေးသာအချိုးတစ်ခုကို တွက်ချက်လိုသည်ဆိုကြပါစို့။

ဆက်စပ်အန္တရာယ်တန်ဖိုးများနှင့်အတူ ဤအတိုးနှုန်းများကို တွက်ချက်ရန်အတွက် SAS ရှိ PROC FREQ နှင့် အောက်ပါအထားအသိုကို chisq နှင့် relrisk လမ်းညွှန်ချက်များဖြင့် အသုံးပြုနိုင်ပါသည်။

 /*create dataset*/
data my_data;
    input result $program $count;
    datalines ;
Passed New 34
Passed Old 39
_Failed New 16
_Failed Old 11
;
run ;
/*calculate odds ratio*/
proc freq data =my_data;
    weightcount ;
    tables program * result / chisq relrisk ;
run ;

ရလဒ်၏ ပထမဇယားတွင် အမျိုးအစားအလိုက် ကိန်းရှင်များ ပေါင်းစပ်မှုတစ်ခုစီ၏ ကြိမ်နှုန်းကို ပြသသည်-

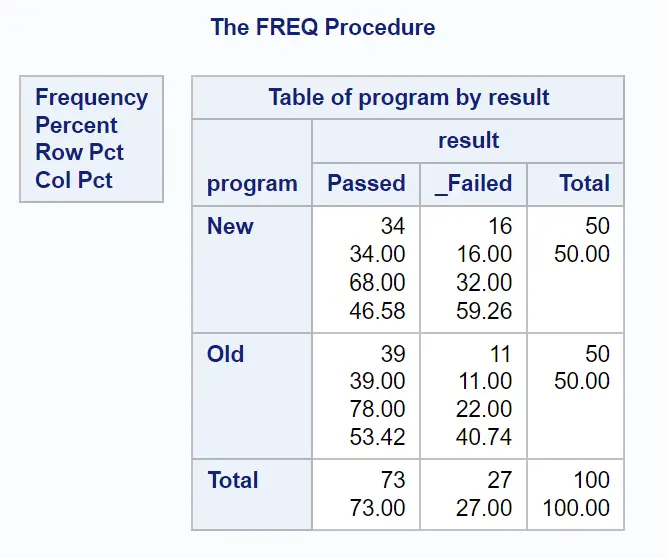
ရလဒ်၏ နောက်ဆုံးဇယားတွင် ကျွန်ုပ်တို့စိတ်ဝင်စားသည့် မသာမယာအချိုးကို ပြသည်-

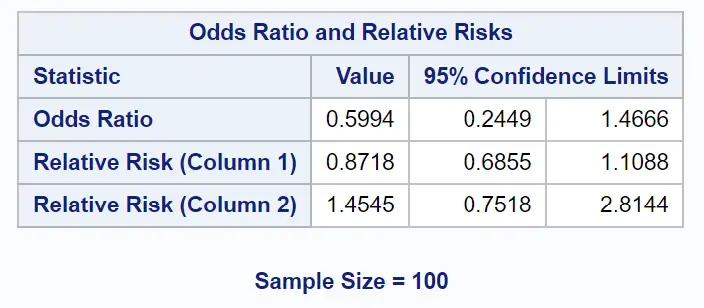
odds အချိုးသည် 0.5994 ဖြစ်သွားသည်။

ပရိုဂရမ်အသစ်ကို အသုံးပြု၍ ပရိုဂရမ်အသစ်ကို အသုံးပြု၍ စာမေးပွဲအောင်မြင်သည့် ကစားသမားတစ်ဦး၏ အခွင့်အလမ်းများသည် ပရိုဂရမ်ဟောင်းကို အသုံးပြု၍ စာမေးပွဲအောင်မြင်သည့် ကစားသမားတစ်ဦး၏ အခွင့်အလမ်းများ 0.5994 ဆ သာရှိသည်ဟု ဆိုလိုခြင်းဖြစ်သည်။

တစ်နည်းဆိုရသော် ပရိုဂရမ်အသစ်ကို အသုံးပြုခြင်းဖြင့် ကစားသမားတစ်ဦး စမ်းသပ်မှုအောင်မြင်နိုင်ခြေကို ခန့်မှန်းခြေအားဖြင့် 40.06% လျော့ကျသွားပါသည်။

ရလဒ် 95% Confidence Limits ကော်လံများတွင်လည်း တန်ဖိုးများကို အသုံးပြုနိုင်ပြီး ကွဲလွဲမှုအချိုးအတွက် အောက်ပါ 95% ယုံကြည်မှုကြားကာလကို တည်ဆောက်နိုင်သည်-

ပေါက်ကြားမှုအချိုးအတွက် 95% ယုံကြည်မှုကြားကာလ- [0.2449, 1.4666] ။

လေ့ကျင့်ရေးပရိုဂရမ်အသစ်နှင့် အဟောင်းကြားရှိ စစ်မှန်သော ကွဲလွဲမှုအချိုးသည် ဤကြားကာလအတွင်းတွင် ရှိနေကြောင်း ကျွန်ုပ်တို့ 95% သေချာပါသည်။

ယုံကြည်မှုကြားကာလတွင် 1 ၏ odds အချိုးတန်ဖိုးများပါ၀င်သောကြောင့်၊ ဆိုလိုသည်မှာ odds အချိုးသည် ကိန်းဂဏန်းအရ သိသာထင်ရှားခြင်းမရှိပါ။

တစ်နည်းဆိုရသော်၊ ပရိုဂရမ်အသစ်ကို အသုံးပြုသည့် ကစားသမားတစ်ဦး၏ အောင်မြင်မှုအခွင့်အလမ်းသည် ပရိုဂရမ်ဟောင်းကို အသုံးပြု၍ အောင်မြင်နိုင်ခြေထက် နည်းပါးကြောင်း ကျွန်ုပ်တို့သိထားသော်လည်း ယင်းအခွင့်အလမ်းများကြား ခြားနားချက်မှာ အမှန်တကယ် ကိန်းဂဏန်းအရ သိသာထင်ရှားခြင်းမရှိပေ။

ထပ်လောင်းအရင်းအမြစ်များ

အောက်ဖော်ပြပါ သင်ခန်းစာများတွင် ထူးထူးခြားခြား အချိုးများအကြောင်း နောက်ထပ်အချက်အလက်များကို ပေးဆောင်သည်-

odds ratio နှင့် relative risk အကြား ခြားနားချက်
ပြီးပြည့်စုံသောလမ်းညွှန်- Odds Ratios ကို မည်သို့အစီရင်ခံမည်နည်း။
အတိုးနှုန်းအချိုးအတွက် ယုံကြည်မှုကြားကာလကို တွက်ချက်နည်း