Sas တွင် skewness & kurtosis တွက်နည်း

ကိန်းဂဏန်းစာရင်းဇယားများတွင်၊ လွဲမှားမှု နှင့် kurtosis သည် ဖြန့်ဖြူးမှုပုံသဏ္ဍာန်ကို တိုင်းတာသည့် နည်းလမ်းနှစ်သွယ်ဖြစ်သည်။

Skewness သည် ဖြန့်ဖြူးမှုတစ်ခု၏ မညီမျှမှုကို တိုင်းတာသည်။

• အနုတ်လက္ခဏာလွဲနေခြင်းက အမြီးသည် ဖြန့်ဖြူးမှု၏ ဘယ်ဘက်ခြမ်းတွင်ရှိကြောင်း ညွှန်ပြသည်။
• အမြီးသည် ဖြန့်ဖြူးမှု၏ ညာဘက်ခြမ်းတွင် ရှိနေကြောင်း အပြုသဘောဆောင်သော စောင်းတံက ဖော်ပြသည်။
• သုည၏တန်ဖိုးသည် ဖြန့်ဖြူးမှုတွင် အချိုးမညီမှုမရှိကြောင်း ညွှန်ပြသည်၊ ဆိုလိုသည်မှာ ဖြန့်ဖြူးမှုသည် လုံးဝအချိုးကျသည်ဟု ဆိုလိုသည်။

Kurtosis သည် ပုံမှန်ဖြန့်ဖြူးမှု တစ်ခုနှင့် နှိုင်းယှဉ်ပါက လေးလံခြင်း သို့မဟုတ် ပေါ့ပါးခြင်းရှိမရှိ တိုင်းတာသည်။

• ပုံမှန်ဖြန့်ဖြူးမှုတစ်ခု၏ kurtosis သည် 0 ဖြစ်သည်။
• ပေးထားသောဖြန့်ဖြူးမှုတစ်ခုတွင် 0 ထက်နည်းသော kurtosis ရှိပါက၊ ၎င်းကို playkurtic ဟုဆိုသည်၊ ဆိုလိုသည်မှာ ၎င်းသည် ပုံမှန်ဖြန့်ဖြူးမှုထက် ပိုနည်းပြီး အစွန်းရောက်အစွန်းထွက်မှုကို ထုတ်ပေးလေ့ရှိသည်။
• ပေးထားသောဖြန့်ဖြူးမှုတစ်ခုတွင် 0 ထက်ကြီးသော kurtosis ရှိပါက၊ ၎င်းကို leptokurtic ဟုဆိုသည်၊ ဆိုလိုသည်မှာ ၎င်းသည် ပုံမှန်ဖြန့်ဖြူးမှုထက် ပိုပိုသာလွန်ကြောင်းကို ဖြစ်ပေါ်စေပါသည်။

SAS ရှိ variable များ၏ skewness နှင့် kurtosis ကိုတွက်ချက်ရန် SKEWNESS နှင့် KURTOSIS ထုတ်ပြန်ချက်များကို PROC MEANS တွင် အသုံးပြုနိုင်သည်။

အောက်ဖော်ပြပါ ဥပမာသည် ဤညွှန်ကြားချက်များကို လက်တွေ့အသုံးချနည်းကို ပြသထားသည်။

ဥပမာ- SAS တွင် Skewness နှင့် Kurtosis တွက်ချက်ခြင်း။

အမျိုးမျိုးသော ဘတ်စကက်ဘောကစားသမားများအကြောင်း အချက်အလက်ပါရှိသော SAS တွင် အောက်ပါဒေတာအစုံရှိသည်ဆိုပါစို့။

 /*create dataset*/
data my_data;
    input team $points assists;
    datalines ;
At 10 2
At 17 5
At 17 6
At 18 3
At 15 0
B 10 2
B 14 5
B 13 4
B 29 0
B 25 2
C 12 1
C 30 1
C 34 3
C 12 4
C 11 7
;
run ;

/*view dataset*/
proc print data =my_data; 

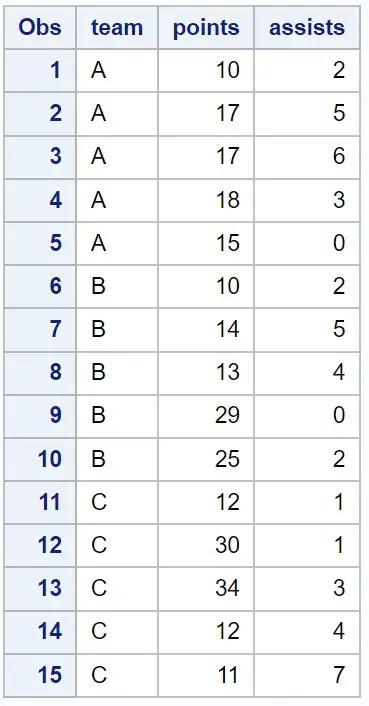
ဒေတာအတွဲရှိ ကိန်းဂဏာန်းတစ်ခုစီ၏ ကွဲလွဲမှုနှင့် kurtosis တို့ကို တွက်ချက်ရန် SKEWNESS နှင့် KURTOSIS ထုတ်ပြန်ချက်များဖြင့် PROC MEANS ကို အသုံးပြုနိုင်ပါသည်။

 /*calculate skewness and kurtosis for each numeric variable*/
proc means data =my_data SKEWNESS KURTOSIS ;
run ; 

အထွက်ဇယားသည် ဒေတာအတွဲရှိ ကိန်းဂဏာန်းကိန်းရှင်တစ်ခုစီအတွက် လွဲချော်မှုနှင့် kurtosis တန်ဖိုးများကို ပြသသည်-

အမှတ် (၁)

• ကိန်းရှင်အမှတ်များသည် 1.009 ၏ လွဲချော်မှု ရှိသည်။ ဤတန်ဖိုးသည် 0 ထက် ကြီးသောကြောင့် အမြီးသည် ဖြန့်ဖြူးမှု၏ ညာဘက်ခြမ်းတွင် ရှိနေသည်ဟု ဆိုလိုသည်။
• အမှတ်များ ပြောင်းလဲနိုင်သော kurtosis သည် -0.299 ရှိသည်။ ဤတန်ဖိုးသည် 0 ထက်နည်းသောကြောင့်၊ ဖြန့်ဖြူးမှုတွင် သာမန်ဖြန့်ဖြူးမှုထက် အနည်းငယ်နည်းပြီး အစွန်းထွက်တန်ဖိုးများ နည်းပါးသည်ဟု ဆိုလိုသည်။

(၂) အကူအညီ

• assists variable သည် 0.304 ၏ skewness ရှိသည်။ ဤတန်ဖိုးသည် 0 ထက် ကြီးသောကြောင့် အမြီးသည် ဖြန့်ဖြူးမှု၏ ညာဘက်ခြမ်းတွင် ရှိနေသည်ဟု ဆိုလိုသည်။
• ပံ့ပိုးမှုကိန်းရှင်တွင် kurtosis -0.782 ရှိသည်။ ဤတန်ဖိုးသည် 0 ထက်နည်းသောကြောင့်၊ ဖြန့်ဖြူးမှုတွင် အထွက်နည်းပြီး ပုံမှန်ဖြန့်ဖြူးမှုထက် လွန်ကဲသောတန်ဖိုးများနည်းသည်ဟု ဆိုလိုသည်။

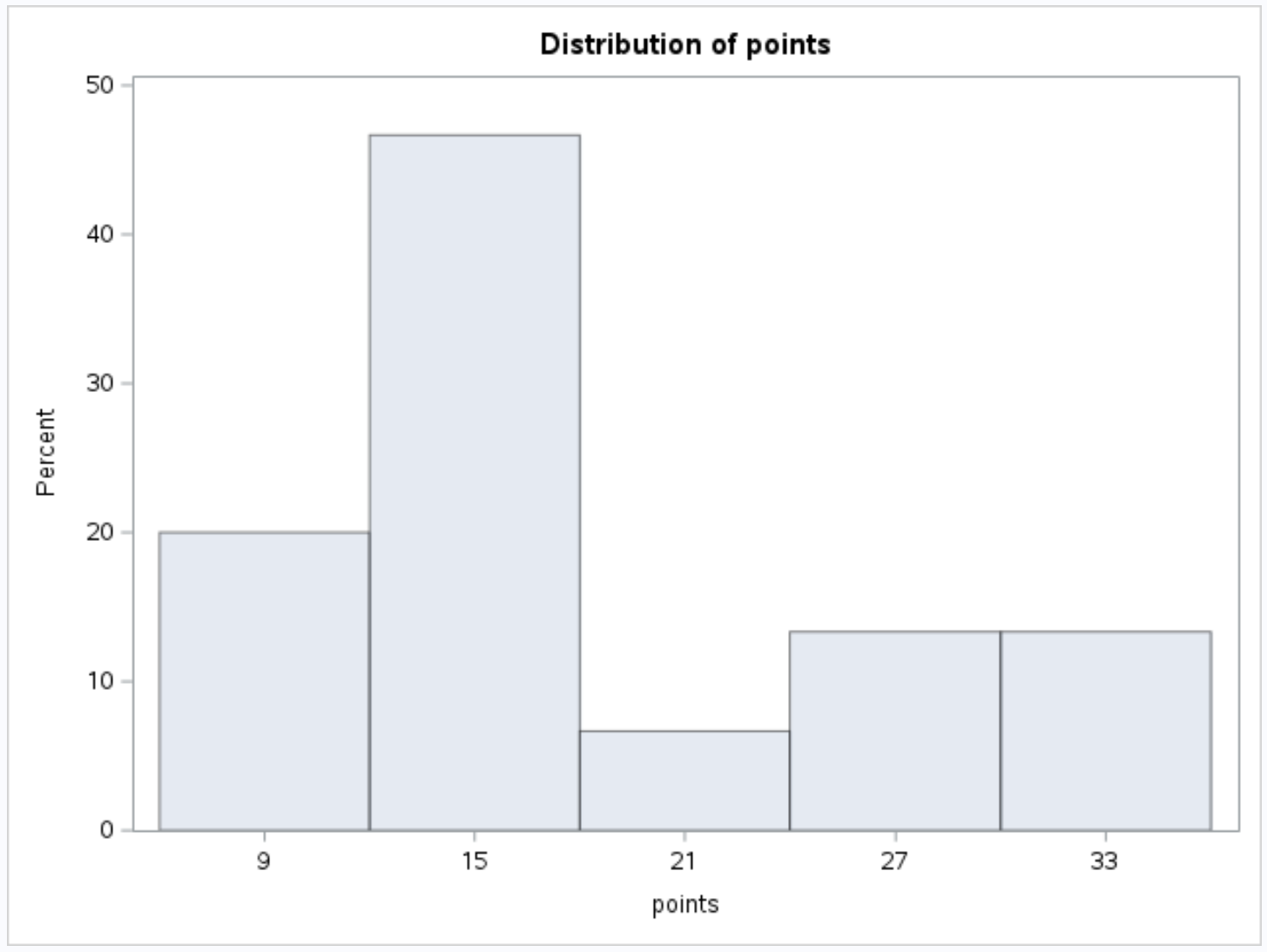
ဒေတာအတွဲရှိ ကိန်းဂဏာန်းကိန်းရှင်တစ်ခုစီအတွက် တန်ဖိုးများ ဖြန့်ဖြူးမှုကို မြင်သာစေရန်၊ အမှတ်အတွက် ဟစ်စတိုဂရမ်များဖန်တီးရန်နှင့် ကိန်းရှင်များကို အထောက်အကူပြုရန် PROC UNIVARIATE ကို သင်အသုံးပြုနိုင်သည်-

 /*create histograms for points and assists variables*/
proc univariate data =my_data;
    var points assists;
    histogram points assists;
run ;

၎င်းသည် အမှတ်များ ပြောင်းလဲနိုင်သော အတွက် အောက်ပါ ဟီစတိုဂရမ်ကို ထုတ်ပေးသည်-

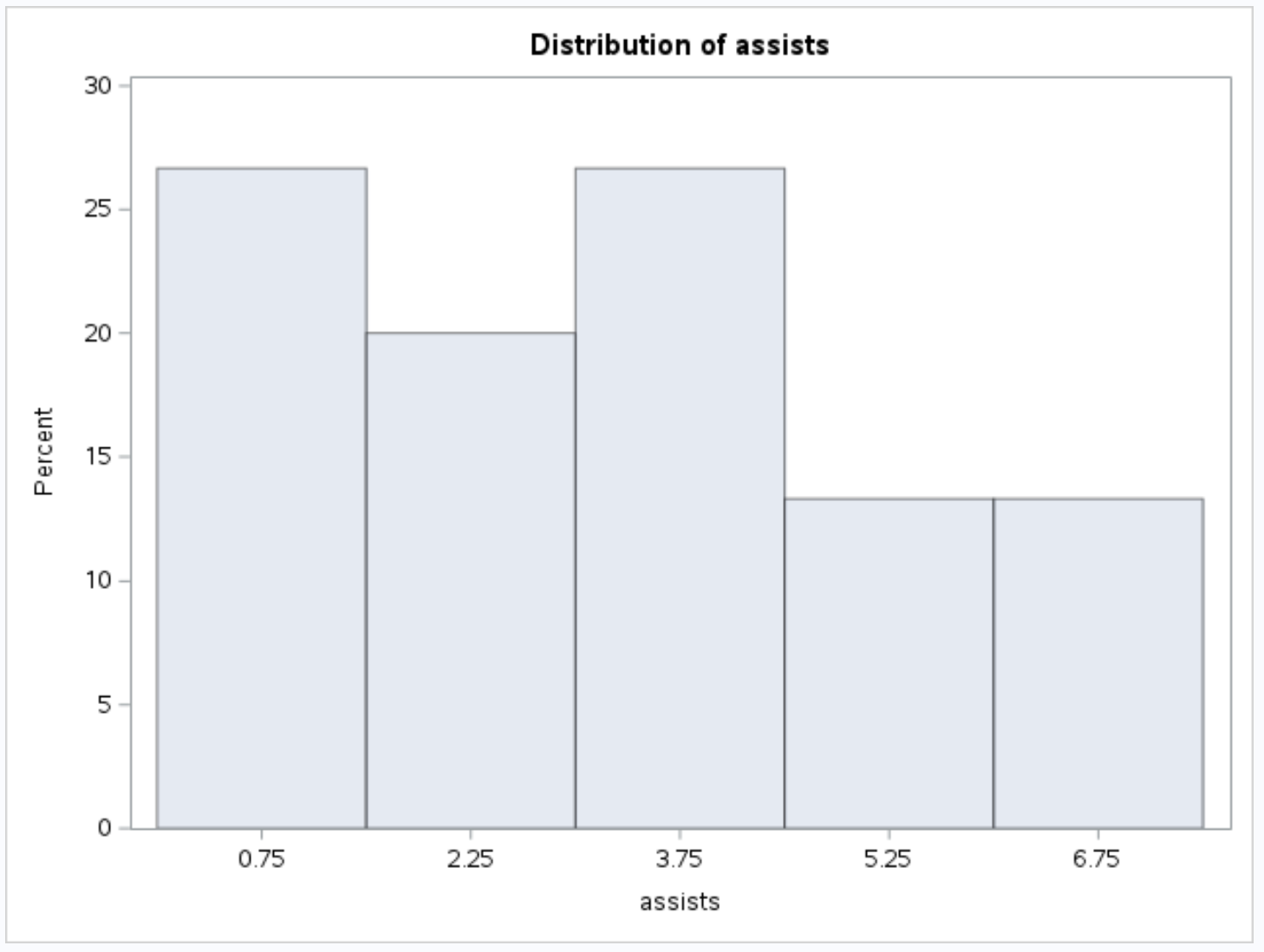
အကူအညီ variable အတွက် အောက်ပါ ဟီစတိုဂရမ်။

ထပ်လောင်းအရင်းအမြစ်များ

အောက်ဖော်ပြပါ သင်ခန်းစာများသည် SAS တွင် အခြားဘုံအလုပ်များကို မည်သို့လုပ်ဆောင်ရမည်ကို ရှင်းပြသည်-

SAS တွင် သရုပ်ဖော်ကိန်းဂဏန်းများ တွက်ချက်နည်း
SAS တွင် ကြိမ်နှုန်းဇယားများ ဖန်တီးနည်း
SAS တွင် ရာခိုင်နှုန်းများ တွက်ချက်နည်း
SAS တွင် PivotTables ဖန်တီးနည်း