Semi-interquartile အပိုင်းအခြား

အားဖြင့် Benjamin Anderson ဩဂုတ် 2, 2023 စာရင်းအင်းများ 0 မှတ်ချက်များ

ဤဆောင်းပါးသည် စာရင်းဇယားများတွင် semi-interquartile အပိုင်းအခြားကို ရှင်းပြထားသည်။ ထို့ကြောင့်၊ semi-interquartile အကွာအဝေးကို တွက်ချက်နည်း၊ ဖြေရှင်းနိုင်သော လေ့ကျင့်ခန်းတစ်ခုနှင့် မည်သည့်ဒေတာနမူနာ၏ semi-interquartile အကွာအဝေးကို တွက်ချက်ရန် အွန်လိုင်းဂဏန်းတွက်စက်ကို သင်တွေ့လိမ့်မည်။

semi-interquartile range ကဘာလဲ။

semi-interquartile အကွာအဝေး (သို့မဟုတ် semi-interquartile အပိုင်းအခြား ) သည် ပထမနှင့် တတိယ quartiles အကြား ထက်ဝက်ကွာခြားသည်။ ထို့ကြောင့်၊ semi-interquartile အပိုင်းအခြားကို တွက်ချက်ရန်၊ သင်သည် တတိယ quartile ကို နုတ်ပြီး ပထမ quartile ကို နုတ်ပြီး နှစ်ဖြင့် ပိုင်းရမည်။

semi-interquartile အကွာအဝေးသည် ဗဟိုတန်ဖိုးများ၏ ကွဲပြားမှုကို ညွှန်ပြသော ပြန့်ကျဲမှုအတိုင်းအတာတစ်ခုဖြစ်သည်။ ထို့ကြောင့်၊ ဒေတာအစုတစ်ခု၏ semi-interquartile အကွာအဝေး ပိုကြီးလေ၊ အလယ်ဗဟိုရှိ တန်ဖိုးများသည် တစ်ခုနှင့်တစ်ခု သက်ဆိုင်လေလေ ဖြစ်သည်။

semi-interquartile အကွာအဝေး၏ ဝိသေသများထဲမှ တစ်ခုမှာ ၎င်းသည် ခိုင်မာသော ကိန်းဂဏန်းဆိုင်ရာ ကန့်သတ်ချက်တစ်ခုဖြစ်ပြီး၊ ထို့ကြောင့် outliers များသည် semi-interquartile အကွာအဝေးကို မထိခိုက်စေပါ။

ထို့ကြောင့်၊ semi-interquartile ကြားကာလသည် ကိန်းဂဏာန်းကြားကာလနှင့် ဆင်တူသော ပြန့်ကျဲနေသော အတိုင်းအတာတစ်ခုဖြစ်ပြီး၊ quartile တန်ဖိုးနှစ်ခုကို နုတ်ခြင်းဖြင့် သတ်မှတ်ဒေတာ၏ ကွဲပြားမှုကို ညွှန်ပြသောကြောင့် ဖြစ်သည်။ သို့သော် ကိန်းဂဏန်းအကွာအဝေးကို တွက်ချက်ရာတွင် အနည်းငယ်ကွဲပြားသည်။

Semi-interquartile အပိုင်းအခြား ဖော်မြူလာ

semi-interquartile အပိုင်းအခြားသည် တတိယ quartile နှင့် ပထမ quartile အကြား ကွာခြားချက်နှင့် ညီမျှပါသည်။ ထို့ကြောင့်၊ semi-interquartile အပိုင်းအခြားကို တွက်ချက်ရန်၊ ပထမနှင့် တတိယ quartile များကို ဦးစွာရှာရမည်ဖြစ်ပြီး ၎င်းတို့ကို နုတ်ကာ နောက်ဆုံးတွင် အနုတ်ရလဒ်ကို နှစ်ပိုင်းခွဲပါ။

ထို့ကြောင့်၊ semi-interquartile အပိုင်းအခြားကို တွက်ချက်ရန် ဖော်မြူလာ မှာ-

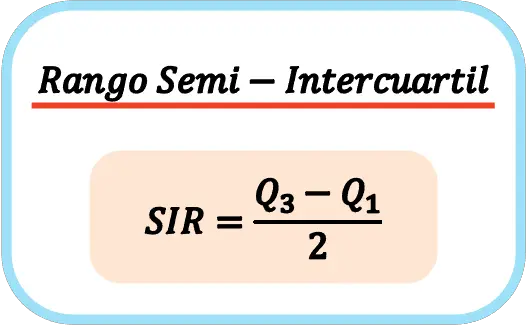
👉 မည်သည့်ဒေတာအစုံ၏ semi-interquartile အကွာအဝေးကို တွက်ချက်ရန် အောက်ပါ ဂဏန်းပေါင်းစက်ကို အသုံးပြုနိုင်သည်။

ယေဘုယျအားဖြင့်၊ semi-interquartile range ကိုကိုယ်စားပြုရန်၊ အတိုကောက် SIR ( Semi Intquartile Range ) ကို ဤစာရင်းအင်းတိုင်းတာမှုအတွက် သင်္ကေတအဖြစ် သုံးလေ့ရှိသည်။

အတိုချုပ်ပြောရလျှင် semi-interquartile range သည် interquartile range ၏ ထက်ဝက်ဖြစ်သည်။

semi-interquartile အပိုင်းအခြားကို တွက်ချက်ခြင်း ဥပမာ

semi-interquartile အကွာအဝေး၏ အဓိပ္ပါယ်ဖွင့်ဆိုချက်နှင့် ၎င်း၏ဖော်မြူလာကို ကြည့်ရှုပြီးနောက်၊ အောက်တွင်၊ semi-interquartile range ကို မည်သို့တွက်ချက်ကြောင်း ရှင်းလင်းစွာ ရှင်းပြရန် အောက်တွင် ခိုင်မာသော ဥပမာတစ်ခုဖြစ်သည်။

ကုမ္ပဏီတစ်ခုတွင် ရင်းနှီးမြုပ်နှံရန် စိတ်ကူးကောင်းရှိမရှိ ကိန်းဂဏန်းများကို ခွဲခြမ်းစိတ်ဖြာလိုပါသည်။ ဒါကိုလုပ်ဖို့၊ ပြီးခဲ့တဲ့ 15 လအတွင်း ဒီကုမ္ပဏီရဲ့ စတော့စျေးနှုန်းဆိုင်ရာ အချက်အလက်တွေကို စုဆောင်းခဲ့ပါတယ်။ အောက်ပါဇယားတွင် အနိမ့်ဆုံးမှ အမြင့်ဆုံးသို့ စီထားသော လေ့လာတွေ့ရှိထားသော အချက်အလက်များကို သင်တွေ့မြင်နိုင်ပါသည်။ ဤဒေတာအစုံ၏ semi-interquartile အပိုင်းအခြားကို တွက်ချက်ပါ။

အထက်တွင်ရှင်းပြထားသည့်အတိုင်း semi-interquartile range ကိုရှာရန်၊ ပထမနှင့်တတိယ quartiles ကို ဦးစွာဆုံးဖြတ်ရပါမည်။

ပထမ quartile သည် တန်ဖိုးများ၏ ပထမနှစ်ဝက်၏ ပျမ်းမျှဖြစ်ပြီး၊ ၎င်းသည် ယူရို 8.95/ရှယ်ယာတန်ဖိုးနှင့် ကိုက်ညီပါသည်။

$Q_1=8,95$

အခြားတစ်ဖက်တွင်၊ တတိယ quartile သည် တန်ဖိုးများ၏ ဒုတိယနှစ်ဝက်၏ အလယ်အလတ်တန်ဖိုးဖြစ်သည်၊ ဆိုလိုသည်မှာ ယူရို 9.83/share ဖြစ်သည်။

$Q_3=9,83$

ပထမနှင့်တတိယ quartile များ၏တန်ဖိုးများကိုကျွန်ုပ်တို့သိသည်နှင့်၎င်း၏တန်ဖိုးကိုရှာဖွေရန် semi-interquartile ကြားကာလအတွက်ဖော်မြူလာကိုရိုးရှင်းစွာအသုံးပြုသည်-

$SIR=\cfrac{Q_3-Q_1}{2}=\cfrac{9,83-8,95}{2}=0,44$

➤ အလယ်အလတ်တန်းစား ကိုကြည့်ပါ။

Semi-interquartile အပိုင်းအခြားဂဏန်းတွက်စက်

၎င်း၏ semi-interquartile အပိုင်းအခြားကို တွက်ချက်ရန် အောက်ပါအွန်လိုင်းဂဏန်းတွက်စက်တွင် သတ်မှတ်ထားသော ကိန်းဂဏန်းအချက်အလက်ကို ထည့်သွင်းပါ။ ဒေတာကို နေရာလွတ်တစ်ခုဖြင့် ပိုင်းခြားထားရမည်ဖြစ်ပြီး ဒဿမပိုင်းခြားခြင်းအဖြစ် ကာလကို အသုံးပြု၍ ထည့်သွင်းရပါမည်။

စာရေးသူအကြောင်း

Benjamin Anderson

မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။