Shapiro-wilk test ကို r ဖြင့် မည်သို့လုပ်ဆောင်ရမည်နည်း (ဥပမာများဖြင့်)

Shapiro-Wilk စစ်ဆေးမှု သည် ပုံမှန်အခြေအနေ၏ စမ်းသပ်မှုဖြစ်သည်။ နမူနာကို ပုံမှန်ဖြန့်ဖြူးမှု မှ လာသလား မဆုံးဖြတ်ရန် ၎င်းကို အသုံးပြုသည်။

ဤစမ်းသပ်မှုအမျိုးအစားသည် ဆုတ်ယုတ်ခြင်း ၊ ANOVA ၊ t-tests နှင့် အခြားများစွာသော ကိန်းဂဏန်းစမ်းသပ်မှုများတွင် အသုံးများသော ယူဆချက်တစ်ခုဖြစ်သည့် ပုံမှန်ဖြန့်ဝေမှုမှ ထွက်ပေါ်လာခြင်းရှိမရှိ ဆုံးဖြတ်ရန်အတွက် အသုံးဝင်သည်။ ‘အခြားသူတွေ။

R တွင် အောက်ပါ built-in လုပ်ဆောင်ချက်ကို အသုံးပြု၍ ပေးထားသည့် ဒေတာအတွဲတစ်ခုတွင် Shapiro-Wilk စမ်းသပ်မှုကို ကျွန်ုပ်တို့ အလွယ်တကူ လုပ်ဆောင်နိုင်သည်-

shapiro.test(x)

ရွှေ-

• x- ဒေတာတန်ဖိုးများ၏ ကိန်းဂဏာန်း vector တစ်ခု။

ဤလုပ်ဆောင်ချက်သည် သက်ဆိုင်ရာ p-value နှင့်အတူ W test statistic ကိုထုတ်ပေးသည်။ p-value သည် α = 0.05 ထက်နည်းပါက၊ နမူနာသည် ပုံမှန်ဖြန့်ဝေထားသော လူဦးရေမှမဟုတ်ဟု ဆိုရန် လုံလောက်သော အထောက်အထားရှိပါသည်။

မှတ်ချက်- shapiro.test() လုပ်ဆောင်ချက်ကို အသုံးပြုရန်အတွက် နမူနာအရွယ်အစားသည် 3 နှင့် 5,000 ကြား ဖြစ်ရပါမည်။

ဤသင်ခန်းစာတွင် ဤလုပ်ဆောင်ချက်ကို လက်တွေ့အသုံးပြုပုံ နမူနာများစွာကို ပြသထားသည်။

ဥပမာ 1- ပုံမှန်ဒေတာအတွက် Shapiro-Wilk စမ်းသပ်မှု

အောက်ပါကုဒ်သည် နမူနာအရွယ်အစား n=100 ပါသော ဒေတာအတွဲတစ်ခုပေါ်တွင် Shapiro-Wilk စမ်းသပ်မှုကို မည်သို့လုပ်ဆောင်ရမည်ကို ပြသသည်-

 #make this example reproducible
set.seed(0)

#create dataset of 100 random values generated from a normal distribution
data <- rnorm(100)

#perform Shapiro-Wilk test for normality
shapiro.test(data)

	Shapiro-Wilk normality test

data:data
W = 0.98957, p-value = 0.6303

စမ်းသပ်မှု၏ p-တန်ဖိုးသည် 0.6303 ဖြစ်လာသည်။ ဤတန်ဖိုးသည် 0.05 ထက်မနည်းသောကြောင့်၊ နမူနာဒေတာသည် ပုံမှန်ဖြန့်ဝေထားသော လူဦးရေမှလာသည်ဟု ကျွန်ုပ်တို့ ယူဆနိုင်ပါသည်။

ပျမ်းမျှ = 0 နှင့် စံသွေဖည် = 1 ဖြင့် ပုံမှန်ဖြန့်ဝေမှုမှ ကျပန်းတန်ဖိုးများကို ထုတ်ပေးသည့် rnorm() လုပ်ဆောင်ချက်ကို အသုံးပြု၍ နမူနာဒေတာကို ထုတ်ပေးသောကြောင့် ဤရလဒ်သည် အံ့သြစရာမဖြစ်သင့်ပါ။

ဆက်စပ်- R တွင် dnorm၊ pnorm၊ qnorm နှင့် rnorm လမ်းညွှန်

နမူနာဒေတာကို ပုံမှန်အတိုင်း ဖြန့်ဝေကြောင်း ရှုမြင်ကြောင်း စစ်ဆေးရန် ဟီစတိုဂရမ်ကိုလည်း ထုတ်လုပ်နိုင်သည်-

 hist(data, col=' steelblue ') 

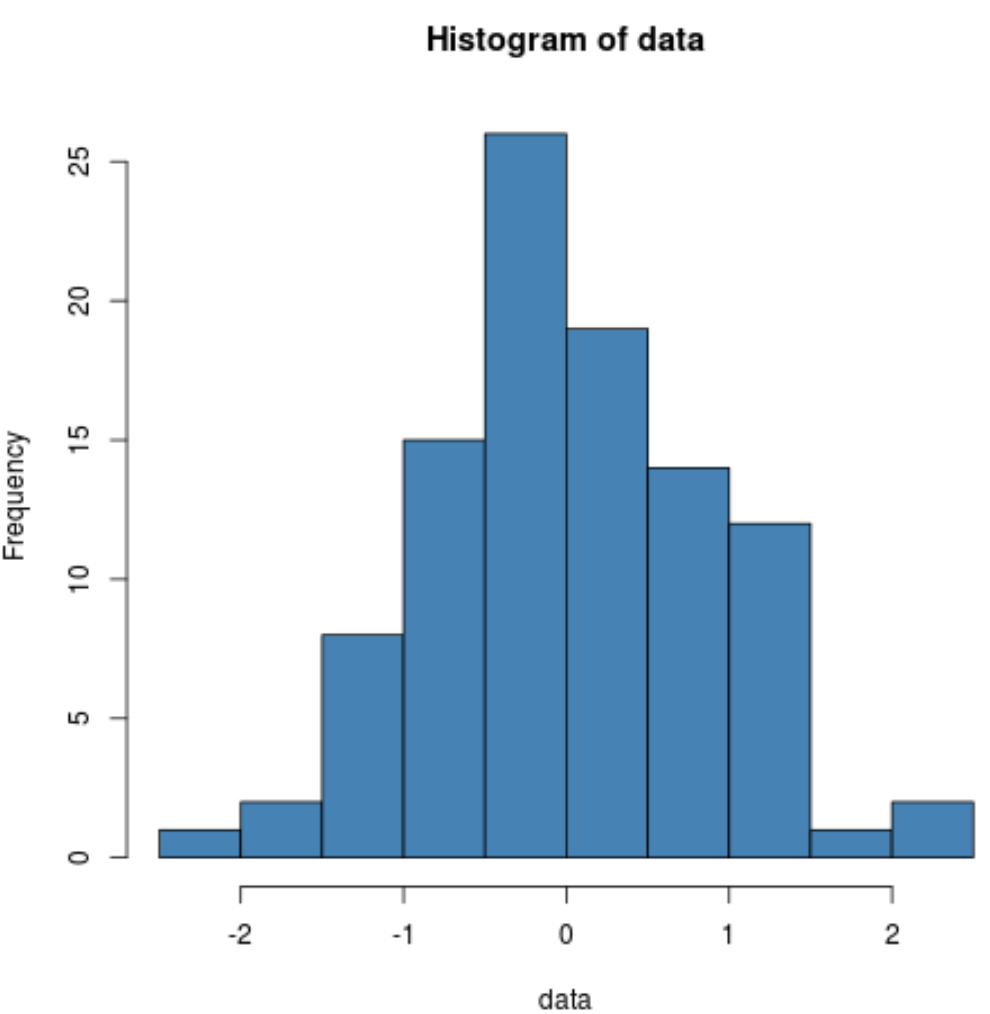
ဖြန့်ဝေမှုမှာ ပုံမှန်အားဖြင့် ဖြန့်ဝေထားသောဒေတာ၏ ပုံမှန်ဖြစ်သည့် ဖြန့်ဖြူးမှု၏ဗဟိုတွင် အထွတ်အထိပ်ဖြင့် အထွတ်အထိပ်ပုံစံဖြင့် ဖြန့်ဖြူးမှုကို ကျွန်ုပ်တို့တွေ့မြင်နိုင်သည်။

ဥပမာ 2- ပုံမှန်မဟုတ်သောဒေတာအတွက် Shapiro-Wilk စမ်းသပ်မှု

အောက်ပါကုဒ်သည် Poisson ဖြန့်ဖြူးမှု မှ တန်ဖိုးများကို ကျပန်းထုတ်ပေးသည့် နမူနာအရွယ်အစား n=100 ပါသည့် ဒေတာအတွဲတစ်ခုတွင် Shapiro-Wilk စမ်းသပ်မှုကို မည်သို့လုပ်ဆောင်ရမည်ကို ပြသသည်-

 #make this example reproducible
set.seed(0)

#create dataset of 100 random values generated from a Poisson distribution
data <- rpois(n=100, lambda=3)

#perform Shapiro-Wilk test for normality
shapiro.test(data)

	Shapiro-Wilk normality test

data:data
W = 0.94397, p-value = 0.0003393

စာမေးပွဲ၏ p-value သည် 0.0003393 ဖြစ်သွားသည်။ ဤတန်ဖိုးသည် 0.05 ထက်နည်းသောကြောင့်၊ နမူနာဒေတာသည် ပုံမှန်ဖြန့်ဝေထားသော လူဦးရေမှ လာမည် မဟုတ်ကြောင်း ပြောရန် လုံလောက်သော အထောက်အထားရှိသည်။

Poisson ဖြန့်ဝေမှုမှ ကျပန်းတန်ဖိုးများကို ထုတ်ပေးသည့် rpois() လုပ်ဆောင်ချက်ကို အသုံးပြု၍ နမူနာဒေတာကို ထုတ်ပေးသောကြောင့် ဤရလဒ်သည် အံ့သြစရာမဟုတ်ပါ။

ဆက်စပ်- R တွင် dpois၊ ppois၊ qpois နှင့် rpois လမ်းညွှန်ချက်

နမူနာဒေတာကို ပုံမှန်ဖြန့်ဝေခြင်းမဟုတ်ကြောင်း မြင်သာမြင်သာစေရန် Histogram ကိုလည်း ထုတ်လုပ်နိုင်သည်-

 hist(data, col=' coral2 ') 

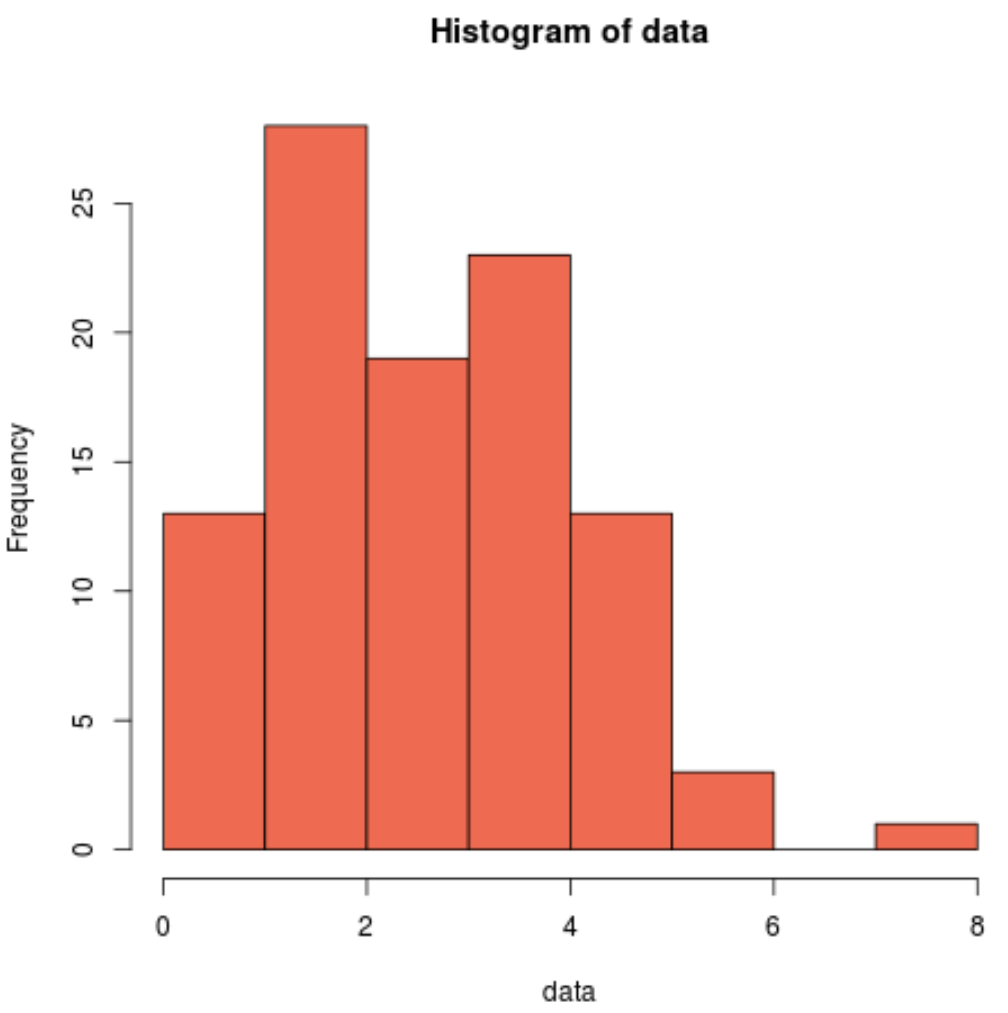
ဖြန့်ချီမှုသည် ညာဘက်စောင်းပြီး ပုံမှန်ဖြန့်ဝေမှုတစ်ခုနှင့် ဆက်စပ်နေသည့် ပုံမှန် “ ခေါင်းလောင်းပုံသဏ္ဍာန်” မပါရှိကြောင်း ကျွန်ုပ်တို့ တွေ့မြင်နိုင်ပါသည်။ ထို့ကြောင့်၊ ကျွန်ုပ်တို့၏ histogram သည် Shapiro-Wilk စမ်းသပ်မှု၏ ရလဒ်များနှင့် ကိုက်ညီပြီး ကျွန်ုပ်တို့၏နမူနာဒေတာသည် ပုံမှန်ဖြန့်ဝေမှုမှ မရောက်ကြောင်း အတည်ပြုပါသည်။

ပုံမှန်မဟုတ်သော ဒေတာဖြင့် ဘာလုပ်ရမည်နည်း။

ပေးထားသည့် ဒေတာအစုံကို ပုံမှန်အတိုင်း မ ဖြန့်ဝေပါက၊ ၎င်းကို ပိုမိုသာမာန်ဖြစ်စေရန် အောက်ပါအသွင်ပြောင်းမှုများထဲမှ တစ်ခုကို ကျွန်ုပ်တို့ မကြာခဏ လုပ်ဆောင်နိုင်သည်-

1. မှတ်တမ်းအသွင်ပြောင်းခြင်း- တုံ့ပြန်မှုကိန်းရှင်ကို y မှ log(y) သို့ ပြောင်းလဲပါ။

2. စတုရန်းအမြစ်အသွင်ပြောင်းခြင်း- တုံ့ပြန်မှုကိန်းရှင်ကို y မှ √y သို့ ပြောင်းလဲပါ။

3. Cube root အသွင်ပြောင်းခြင်း- တုံ့ပြန်မှု variable ကို y မှ y ^1/3 သို့ပြောင်းပါ။

ဤအသွင်ပြောင်းမှုများကို လုပ်ဆောင်ခြင်းဖြင့်၊ တုံ့ပြန်မှုကိန်းရှင်သည် ယေဘုယျအားဖြင့် ပုံမှန်ဖြန့်ဝေမှုကို အနီးစပ်ဆုံး ခန့်မှန်းသည်။

ဤပြောင်းလဲမှုများကို လက်တွေ့တွင် မည်သို့လုပ်ဆောင်ရမည်ကို ကြည့်ရှုရန် ဤသင်ခန်းစာကို ကြည့်ပါ။

ထပ်လောင်းအရင်းအမြစ်များ

R တွင် Anderson-Darling စမ်းသပ်မှုပြုလုပ်နည်း
R တွင် Kolmogorov-Smirnov စမ်းသပ်မှုပြုလုပ်နည်း
Python တွင် Shapiro-Wilk Test ကို မည်သို့လုပ်ဆောင်ရမည်နည်း။