Snedecor f ဖြန့်ဝေခြင်း။
ဤဆောင်းပါးတွင် Snedecor F ဖြန့်ဖြူးမှုသည် အဘယ်အရာနှင့် ၎င်းကိုအသုံးပြုကြောင်း ရှင်းပြထားသည်။ ထို့အပြင်၊ Snedecor F ဖြန့်ဖြူးမှုဂရပ်နှင့် ၎င်း၏ ကိန်းဂဏန်းဂုဏ်သတ္တိများကို သင်တွေ့မြင်နိုင်မည်ဖြစ်သည်။
Snedecor F ဖြန့်ဖြူးမှုကား အဘယ်နည်း။
Snedecor F ဖြန့်ဖြူးမှုသည် Fisher-Snedecor F ဖြန့်ဖြူးမှု သို့မဟုတ် ရိုးရိုး F ဖြန့်ဝေခြင်း ဟုလည်း ခေါ်သည် ၊ အထူးသဖြင့် ကွဲပြားမှုကို ခွဲခြမ်းစိတ်ဖြာရာတွင် အသုံးပြုသည့် ဆက်တိုက်ဖြစ်နိုင်ခြေဖြန့်ဝေမှုတစ်ခုဖြစ်သည်။
Snedecor F ဖြန့်ဖြူးမှု၏ ဂုဏ်သတ္တိများထဲမှ တစ်ခုမှာ ၎င်းတို့၏ လွတ်လပ်မှုဒီဂရီများကို ညွှန်ပြသည့် အစစ်အမှန် ဘောင်နှစ်ခုဖြစ်သည့် m နှင့် n တို့၏ တန်ဖိုးဖြင့် သတ်မှတ်ခြင်းဖြစ်သည်။ ထို့ကြောင့်၊ Snedecor ဖြန့်ချီမှု F အတွက် သင်္ကေတသည် F m၊n ဖြစ်ပြီး m နှင့် n သည် ဖြန့်ဖြူးမှုကို သတ်မှတ်ပေးသည့် ဘောင်များဖြစ်သည်။

![Rendered by QuickLaTeX.com \left.\begin{array}{c} X\sim \chi_m^2\\[2ex] Y\sim \chi_n^2\end{array}\right\}\color{orange}\bm{\longrightarrow}\color{black}\ F_{m,n}= \cfrac{X/m}{Y/n}](https://statorials.org/wp-content/ql-cache/quicklatex.com-d407869e61ca4357ffbcb40df3bd83ab_l3.png)
Fisher-Snedecor F ဖြန့်ချီမှုသည် အင်္ဂလိပ်စာရင်းအင်းပညာရှင် Ronald Fisher နှင့် အမေရိကန်စာရင်းအင်းပညာရှင် George Snedecor တို့ထံ ပေးဆောင်ထားသည်။
စာရင်းဇယားများအရ Fisher-Snedecor F ဖြန့်ဖြူးမှုတွင် မတူညီသော အပလီကေးရှင်းများရှိသည်။ ဥပမာအားဖြင့်၊ Fisher-Snedecor F ဖြန့်ဖြူးမှုကို မတူညီသော မျဉ်းကြောင်းဆုတ်ယုတ်မှုပုံစံများကို နှိုင်းယှဉ်ရန်အတွက် အသုံးပြုပြီး ဤဖြစ်နိုင်ခြေဖြန့်ဝေမှုကို ကွဲလွဲမှု (ANOVA) ခွဲခြမ်းစိတ်ဖြာမှုတွင် အသုံးပြုပါသည်။
Snedecor F ဖြန့်ဖြူးမှု ပုံကြမ်း
Snedecor F ဖြန့်ဖြူးမှု၏ အဓိပ္ပါယ်ဖွင့်ဆိုချက်ကို ကျွန်ုပ်တို့မြင်ပြီးသည်နှင့်၊ ၎င်း၏သိပ်သည်းဆလုပ်ဆောင်မှု၏ဂရပ်နှင့် ၎င်း၏ စုစည်းဖြစ်နိုင်ခြေ၏ဂရပ်ကို အောက်တွင်ပြသထားသည်။
အောက်ဖော်ပြပါဂရပ်တွင် လွတ်လပ်မှုဒီဂရီအမျိုးမျိုးဖြင့် Snedecor F ဖြန့်ဝေမှုများ၏နမူနာများစွာကို သင်တွေ့မြင်နိုင်ပါသည်။
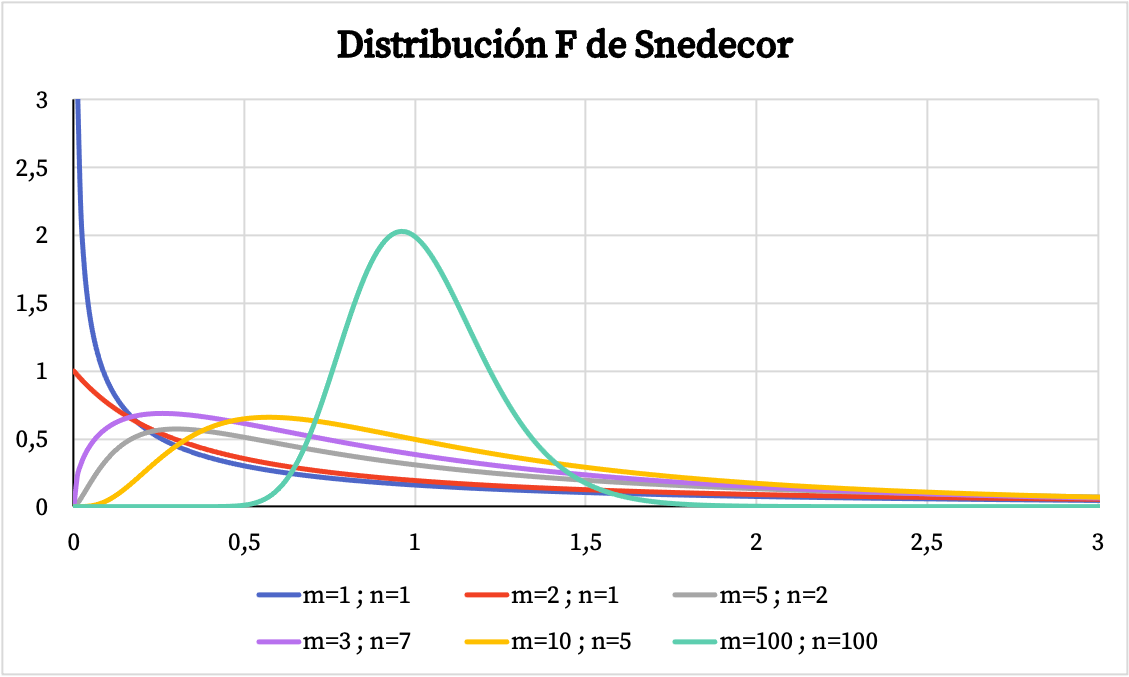
အခြားတစ်ဖက်တွင်၊ အောက်ဖော်ပြပါဂရပ်တွင် Snedecor F ဖြန့်ဖြူးမှု၏ တိုးပွားလာနိုင်သည့် ဖြစ်နိုင်ခြေရှိသော ဂရပ်သည် ၎င်း၏ဝိသေသတန်ဖိုးများပေါ်မူတည်၍ မည်သို့ကွဲပြားသည်ကို သင်တွေ့မြင်နိုင်ပါသည်။
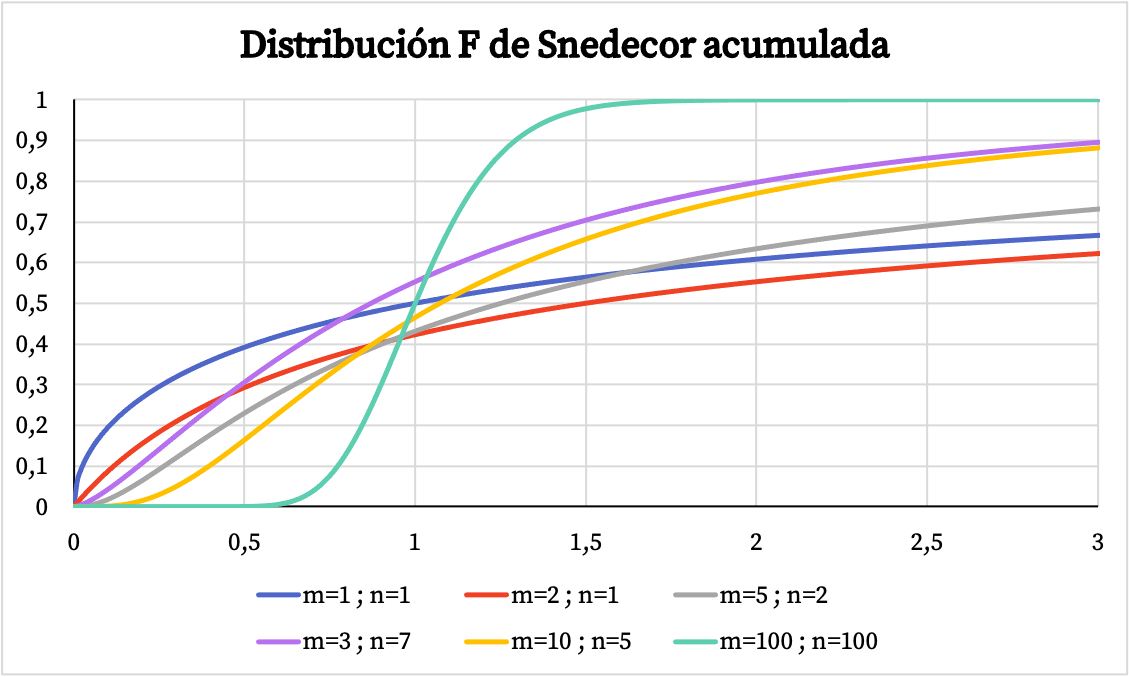
Snedecor F ဖြန့်ဖြူးခြင်း၏ လက္ခဏာများ
နောက်ဆုံးတွင်၊ ဤကဏ္ဍသည် Snedecor F ဖြန့်ဖြူးမှု၏ အရေးကြီးဆုံးသောလက္ခဏာများကို တင်ဆက်ထားသည်။
- Snedecor F ဖြန့်ဖြူးမှု၏ လွတ်လပ်မှုဒီဂရီ၊ m နှင့် n သည် ဖြန့်ဖြူးမှု၏ပုံသဏ္ဍာန်ကို သတ်မှတ်ပေးသည့် ဘောင်နှစ်ခုဖြစ်သည်။ Snedecor F ဖြန့်ဖြူးမှု၏ ဤလက္ခဏာတန်ဖိုးများသည် အပြုသဘောဆောင်သော ကိန်းပြည့်များဖြစ်သည်။
![\begin{array}{c}m,n \in \mathbb{Z}\\[2ex] m,n>0\end{array}” title=” Rendered by QuickLaTeX.com” height=” 54″ width=” 68″ style=” vertical-align: 0px;” ></p>
</p>
<ul>
<li> Snedecor F ဖြန့်ဖြူးမှု၏ ဒိုမိန်းတွင် သုညထက်ကြီးသော သို့မဟုတ် ညီမျှသော ကိန်းဂဏာန်းများအားလုံး ပါဝင်သည်။</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-043df156b055e7088fa83fe733825632_l3.png)
![]()
- n 2 ထက်ကြီးသောတန်ဖိုးများအတွက်၊ Snedecor F ဖြန့်ဖြူးမှု၏ပျမ်းမျှသည် n အနှုတ် 2 ၏နုတ်တွင် n နှင့်ညီမျှသည်။
![\begin{array}{c}X\sim F_{m,n}\\[2ex] E[X]=\cfrac{n}{n-2} \qquad \text{para }n>2\end{array} ” title=” Rendered by QuickLaTeX.com” height=” 75″ width=” 225″ style=” vertical-align: 0px;” ></p>
</p>
<ul>
<li> သတ်မှတ်ချက် <em>n</em> သည် 2 ထက် ကြီးသောအခါ၊ Snedecor ဖြန့်ဖြူးမှု F ၏ ကွဲလွဲမှုကို အောက်ပါဖော်မြူလာကို အသုံးပြုခြင်းဖြင့် တွက်ချက်နိုင်သည်-</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-5861b8fbc6e7aef8cac0eb21cad00c9f_l3.png)
![\begin{array}{c}X\sim F_{m,n}\\[2ex] Var(X)=\cfrac{2n^2\cdot (m+n-2)}{m\cdot (n-2)^2\cdot (n-4)} \qquad \text{para }n>4\end{array} ” title=” Rendered by QuickLaTeX.com” height=” 80″ width=” 366″ style=” vertical-align: 0px;” ></p>
</p>
<ul>
<li> ကန့်သတ်ဘောင် <em>m</em> သည် 2 ထက် ကြီးပါက၊ Snedecor ဖြန့်ချီရေး F ၏ မုဒ်ကို အောက်ပါ စကားရပ်ဖြင့် တွက်ချက်နိုင်သည်-</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-9a284413da889eec7ac2e9a95e255169_l3.png)
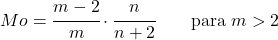
![Rendered by QuickLaTeX.com \displaystyle P[X=x]=\frac{\Gamma\left(\frac{m+n}{2}\right)}{\Gamma\left(\frac{m}{2}\right)\Gamma\left(\frac{n}{2}\right)}\left(\frac{m}{n}\right)^{\frac{m}{2}}\cdot\frac{x^{\frac{m-2}{2}}}{\left(1+\frac{mx}{n}\right)^{\frac{m+n}{2}}}](https://statorials.org/wp-content/ql-cache/quicklatex.com-06871a7baaf462b75f545a02eac7dd11_l3.png)
- ကိန်းရှင်တစ်ခုသည် လွတ်လပ်မှုဒီဂရီ m နှင့် n ဖြင့် Snedecor F ဖြန့်ဖြူးမှုကို လိုက်နာပါက၊ ထိုကိန်းရှင်၏ ပြောင်းပြန်သည် Snedecor F ဖြန့်ဖြူးမှုနောက်တွင် တူညီသောလွတ်လပ်မှုဒီဂရီနှင့် ၎င်း၏တန်ဖိုးများကို အစီအစဥ်ပြောင်းလဲစေသည်။
![]()
- ကျောင်းသား ဖြန့်ဖြူးမှုတွင် Snedecor F ဖြန့်ဖြူးမှုနှင့် အောက်ပါ ဆက်ဆံရေး ရှိသည်။
![]()