Spss တွင် မျဉ်းကြောင်းပြန်ဆုတ်မှု အများအပြားကို မည်သို့လုပ်ဆောင်ရမည်နည်း။

Multiple linear regression သည် နှစ်ခု သို့မဟုတ် နှစ်ခုထက်ပိုသော explanatory variable နှင့် response variable အကြား ဆက်နွယ်မှုကို နားလည်ရန် ကျွန်ုပ်တို့ အသုံးပြုနိုင်သည့် နည်းလမ်းတစ်ခုဖြစ်သည်။

ဤသင်ခန်းစာတွင် SPSS တွင် linear regression မျိုးစုံကို မည်သို့လုပ်ဆောင်ရမည်ကို ရှင်းပြထားသည်။

ဥပမာ- SPSS ရှိ Multiple Linear Regression

စာကျက်ချိန်နာရီအရေအတွက်နှင့် စာမေးပွဲဖြေဆိုသည့် အကြိမ်အရေအတွက်သည် ပေးထားသည့် စာမေးပွဲတွင် ကျောင်းသားလက်ခံသည့် အတန်းအပေါ် သက်ရောက်မှုရှိမရှိ သိချင်သည်ဆိုပါစို့။ ၎င်းကိုလေ့လာရန်၊ အောက်ဖော်ပြပါ variable များကိုအသုံးပြု၍ linear regression အများအပြားလုပ်ဆောင်နိုင်သည်-

ရှင်းပြချက် ကိန်းရှင်များ-

• နာရီများကို လေ့လာခဲ့သည်။
• အကြို စာမေးပွဲတွေ ပြီးတယ်။

တုံ့ပြန်မှုပြောင်းလဲနိုင်သော

• စာမေးပွဲရလဒ်

SPSS တွင် ဤမျဉ်းကြောင်းအတိုင်း ဆုတ်ယုတ်မှုများစွာကို လုပ်ဆောင်ရန် အောက်ပါအဆင့်များကို အသုံးပြုပါ။

အဆင့် 1: ဒေတာကိုထည့်ပါ။

သင်ကြားခဲ့သည့် နာရီအရေအတွက်၊ ကြိုတင်ပြင်ဆင်မှုစာမေးပွဲများနှင့် ကျောင်းသား 20 အတွက် လက်ခံရရှိသော စာမေးပွဲရလဒ်များအတွက် အောက်ပါဒေတာကို ထည့်သွင်းပါ-

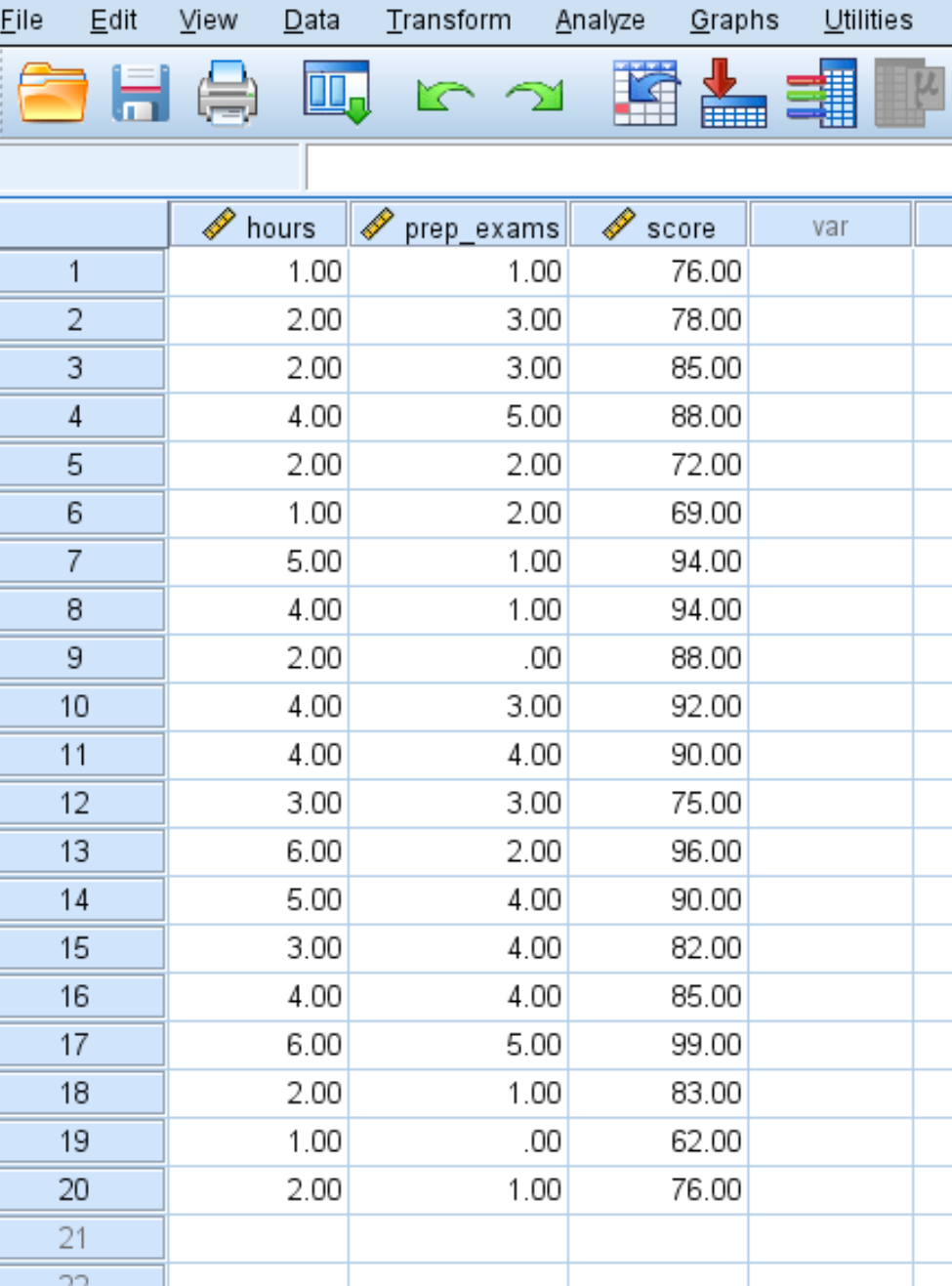
အဆင့် 2- မျဉ်းကြောင်းအတိုင်း ဆုတ်ယုတ်မှုများစွာကို လုပ်ဆောင်ပါ။

Analyze tab ကိုနှိပ်ပါ၊ ထို့နောက် Regression ၊ ထို့နောက် Linear :

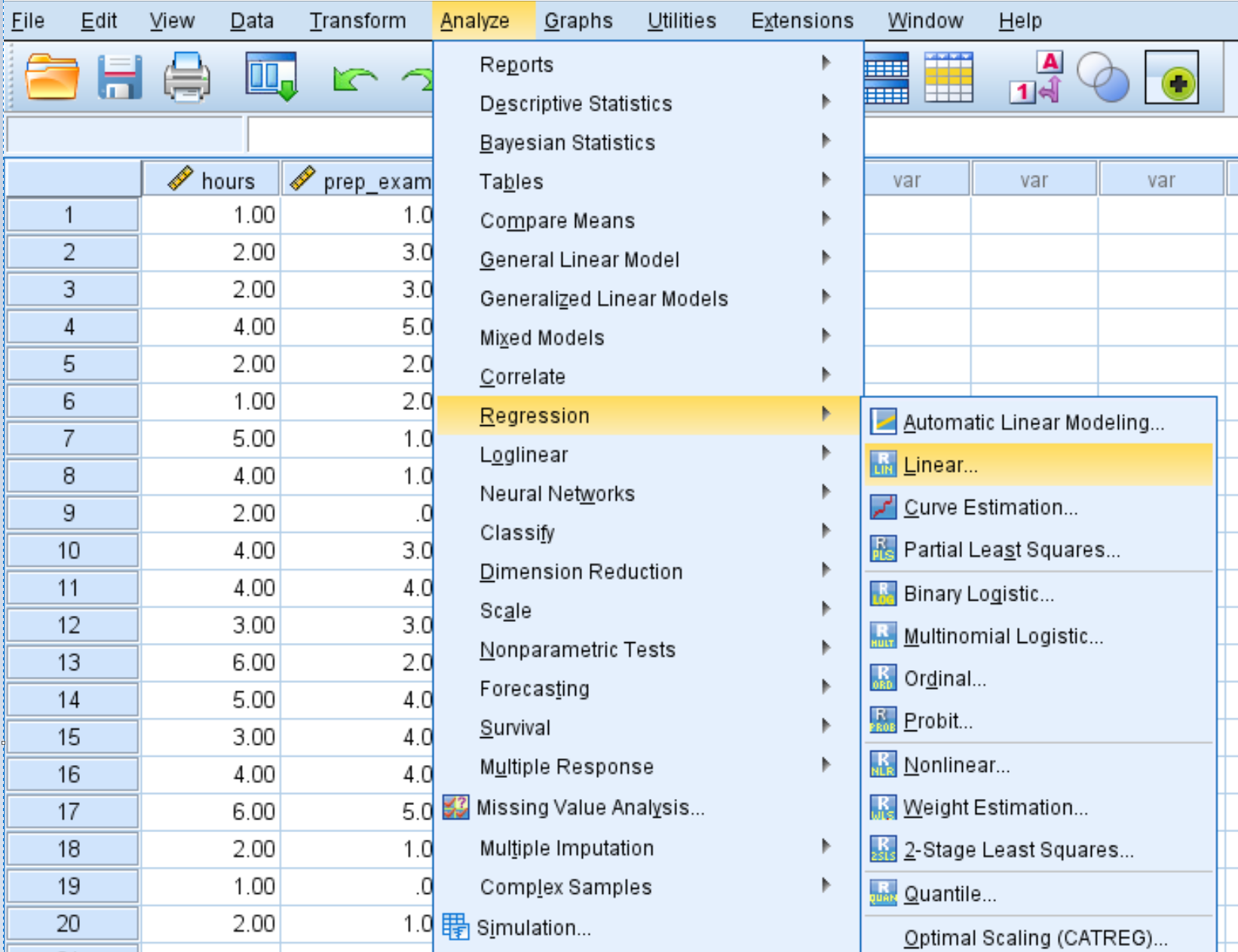
Dependent ဟုအမည်တပ်ထားသော အကွက်ထဲသို့ ပြောင်းလဲနိုင်သော ရမှတ်ကို ဆွဲယူပါ။ Independent(s) တံဆိပ်တပ်ထားသော အကွက်ထဲသို့ နာရီ နှင့် prep_exam ကိန်းရှင်များကို ဆွဲယူပါ။ ထို့နောက် OK ကိုနှိပ်ပါ။

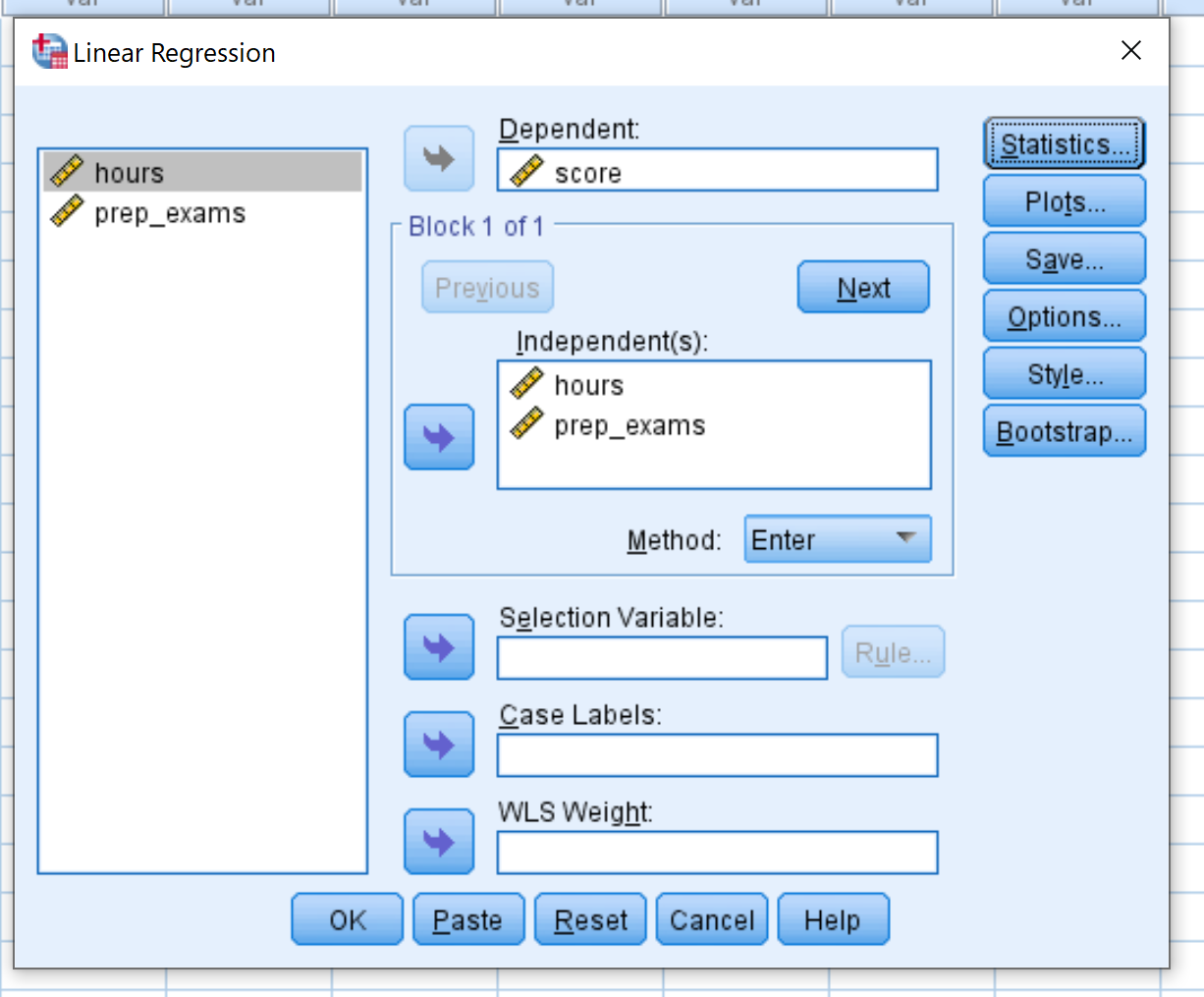
အဆင့် 3- ရလဒ်ကို ဘာသာပြန်ပါ။

OK ကို နှိပ်လိုက်သည်နှင့်၊ များစွာသော linear regression ရလဒ်များသည် window အသစ်တစ်ခုတွင် ပေါ်လာမည်ဖြစ်သည်။

ကျွန်ုပ်တို့စိတ်ဝင်စားသော ပထမဇယားကို Model Summary ဟုခေါ်သည် ။

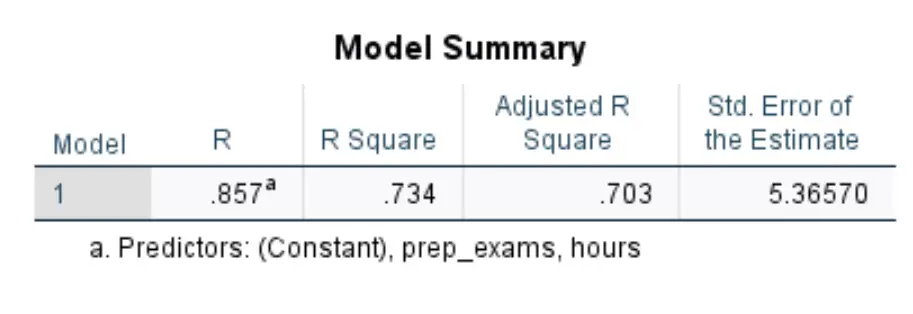
ဤဇယားရှိ အသက်ဆိုင်ဆုံးနံပါတ်များကို မည်သို့အဓိပ္ပာယ်ပြန်ဆိုရမည်ကို ဤတွင်ဖော်ပြထားသည်-

• R Square- ဤသည်မှာ ရှင်းလင်းချက် ကိန်းရှင်များဖြင့် ရှင်းပြနိုင်သော တုံ့ပြန်မှုကိန်းရှင်ရှိ ကွဲလွဲမှု၏ အချိုးအစားဖြစ်သည်။ ဤဥပမာတွင်၊ စာမေးပွဲရမှတ်များ ကွဲလွဲမှု၏ 73.4% ကို နာရီနှင့် ကြိုတင်ပြင်ဆင်ထားသော စာမေးပွဲအရေအတွက်ဖြင့် ရှင်းပြနိုင်သည်။
• စံ။ ခန့်မှန်းချက်အမှား- စံအမှား သည် သတိပြုမိသောတန်ဖိုးများနှင့် ဆုတ်ယုတ်မှုမျဉ်းကြားရှိ ပျမ်းမျှအကွာအဝေးဖြစ်သည်။ ဤဥပမာတွင်၊ လေ့လာထားသောတန်ဖိုးများသည် ဆုတ်ယုတ်မှုမျဉ်းမှ ပျမ်းမျှယူနစ် 5.3657 ဖြင့် သွေဖည်သွားပါသည်။

ကျွန်ုပ်တို့စိတ်ဝင်စားသော နောက်ဇယားကို ANOVA ဟုခေါ်သည်။

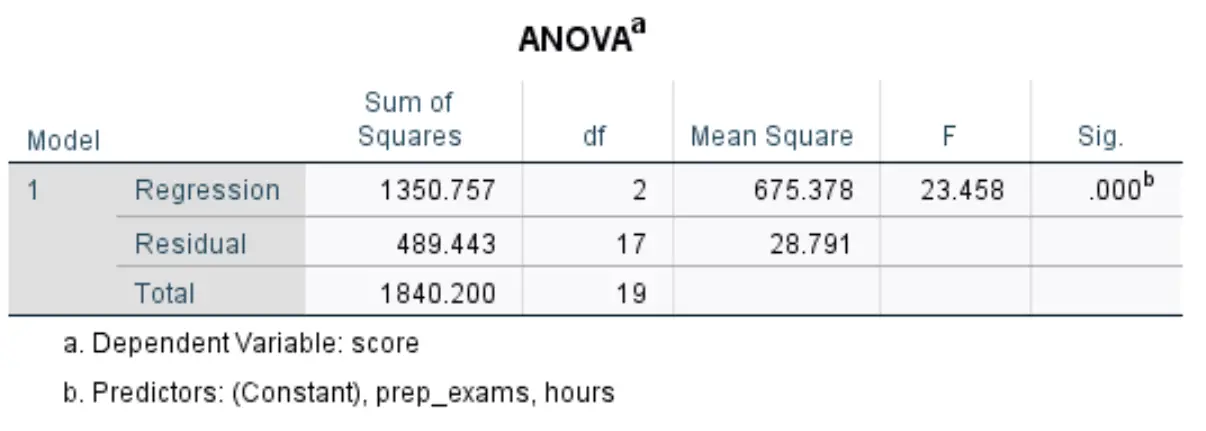
ဤဇယားရှိ အသက်ဆိုင်ဆုံးနံပါတ်များကို မည်သို့အဓိပ္ပာယ်ပြန်ဆိုရမည်ကို ဤတွင်ဖော်ပြထားသည်-

• F- ဤသည်မှာ Mean Square Regression / Mean Square Residual အဖြစ် တွက်ချက်ထားသော ဆုတ်ယုတ်မှုပုံစံအတွက် အလုံးစုံ F ကိန်းဂဏန်းဖြစ်သည်။
• Sig- ဤသည်မှာ အလုံးစုံ F ကိန်းဂဏန်းနှင့်ဆက်စပ်နေသည့် p-တန်ဖိုးဖြစ်သည်။ ၎င်းသည် ဆုတ်ယုတ်မှုပုံစံတစ်ခုလုံးအား ကိန်းဂဏန်းအချက်အလတ်အရ သိသာထင်ရှားမှုရှိ၊ မရှိ ကျွန်ုပ်တို့အား ပြောပြသည်။ တစ်နည်းအားဖြင့်၊ ရှင်းပြချက်နှစ်ခုပေါင်းစပ်ထားသော ကိန်းရှင်နှစ်ခုသည် တုံ့ပြန်မှုကိန်းရှင်နှင့် ကိန်းဂဏန်းအရ သိသာထင်ရှားသော ဆက်စပ်မှုရှိမရှိကို ပြောပြသည်။ ဤကိစ္စတွင်၊ p-value သည် 0.000 နှင့် ညီမျှသည်၊ ၎င်းသည် ရှင်းပြထားသော variables များ၊ လေ့လာထားသော နာရီများနှင့် ကြိုတင်ပြင်ဆင်ထားသော စာမေးပွဲများသည် စာမေးပွဲရလဒ်နှင့် ကိန်းဂဏန်းအရ သိသာထင်ရှားစွာ ဆက်စပ်မှုရှိသည်ကို ညွှန်ပြပါသည်။

ကျွန်ုပ်တို့စိတ်ဝင်စားသော အောက်ပါဇယားသည် Coefficients ခေါင်းစဉ်ဖြစ်သည်။

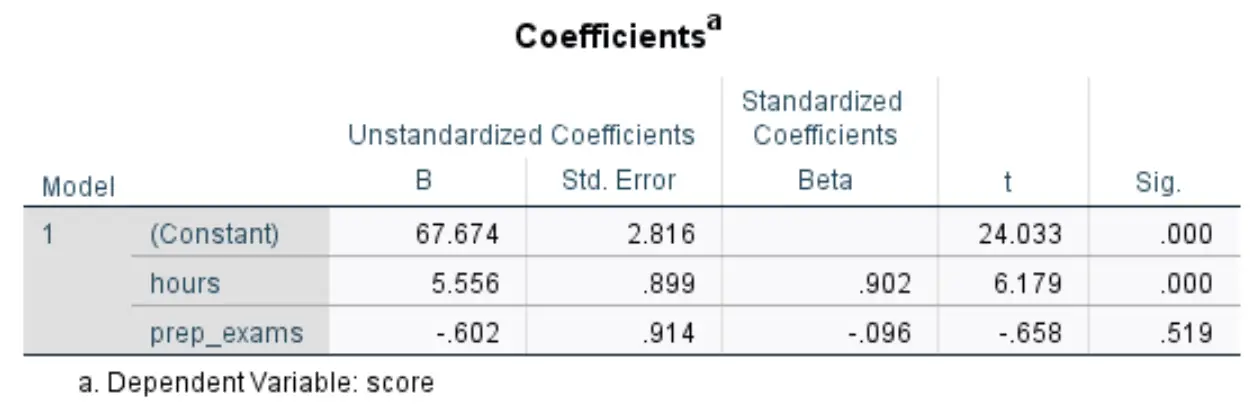
ဤဇယားရှိ အသက်ဆိုင်ဆုံးနံပါတ်များကို မည်သို့အဓိပ္ပာယ်ပြန်ဆိုရမည်ကို ဤတွင်ဖော်ပြထားသည်-

• B စံချိန်စံညွှန်းမရှိသော (ကိန်းသေ)- ခန့်မှန်းသူကိန်းရှင်နှစ်ခုလုံးသည် သုညဖြစ်သောအခါ ၎င်းသည် ကျွန်ုပ်တို့အား တုံ့ပြန်မှုကိန်းရှင်၏ ပျမ်းမျှတန်ဖိုးကို ပြောပြသည်။ ဤဥပမာတွင်၊ နာရီပိုင်းလေ့လာပြီး ကြိုတင်ပြင်ဆင်သည့်စာမေးပွဲနှစ်ခုစလုံးသည် သုညဖြစ်နေသောအခါ ပျမ်းမျှစာမေးပွဲရမှတ်မှာ 67,674 ဖြစ်သည်။
• စံချိန်စံညွှန်းမမီသော B (နာရီများ)- ၎င်းသည် လေ့လာမှုနာရီများတွင် တစ်ယူနစ်တိုးခြင်းနှင့် ဆက်စပ်သော စာမေးပွဲရမှတ်များ၏ ပျမ်းမျှပြောင်းလဲမှုကို ကျွန်ုပ်တို့အား ပြောပြသည်၊၊ ကြိုတင်ပြင်ဆင်ထားသော စာမေးပွဲအရေအတွက်သည် ဆက်တိုက်ရှိနေသည်ဟု ယူဆပါသည်။ ဤကိစ္စတွင်၊ စာကျက်ချိန် နောက်ထပ်တစ်နာရီတိုင်းသည် စာမေးပွဲရမှတ် 5,556 မှတ် တိုးလာခြင်းနှင့် ဆက်စပ်နေပြီး၊ ဖြေဆိုခဲ့သော အလေ့အကျင့်စာမေးပွဲများ အရေအတွက်သည် စဉ်ဆက်မပြတ်ရှိနေသည်ဟု ယူဆပါသည်။
• စံချိန်စံညွှန်းမမီသော B (prep_exams)- ၎င်းသည် ဖြေဆိုထားသော ကြိုတင်စာမေးပွဲများတွင် တစ်ယူနစ်တိုးလာခြင်းနှင့် ဆက်စပ်သော စာမေးပွဲရမှတ်တွင် ပျမ်းမျှပြောင်းလဲမှုကို ပြောပြသည်၊၊ လေ့လာသည့်နာရီအရေအတွက်သည် အမြဲမပြတ်ရှိနေသည်ဟု ယူဆပါသည်။ ဤကိစ္စတွင်၊ ဖြေဆိုခဲ့သော နောက်ထပ်ကြိုတင်ပြင်ဆင်မှုတစ်ခုစီသည် စာမေးပွဲရမှတ်တွင် 0.602 မှတ် လျော့ကျသွားခြင်းနှင့် ဆက်စပ်နေသောကြောင့် သင်ကြားခဲ့သည့် နာရီအရေအတွက်သည် စဉ်ဆက်မပြတ်ရှိနေသည်ဟု ယူဆပါသည်။
• ဆိုင်းဘုတ်။ (နာရီ) : ဤသည်မှာ ရှင်းလင်းချက်ပြောင်းနိုင်သော နာရီ များအတွက် p-တန်ဖိုးဖြစ်သည်။ ဤတန်ဖိုး (0.000) သည် 0.05 ထက်နည်းသောကြောင့်၊ လေ့လာသည့်နာရီများသည် စာမေးပွဲရမှတ်များနှင့် စာရင်းအင်းအရ သိသာထင်ရှားသောဆက်စပ်မှုရှိသည်ဟု ကျွန်ုပ်တို့ကောက်ချက်ချနိုင်ပါသည်။
• ဆိုင်းဘုတ်။ (prep_exams): ဤသည်မှာ prep_exams ၏ ရှင်းလင်းချက်ပြောင်းနိုင်သော variable အတွက် p-value ဖြစ်သည်။ ဤတန်ဖိုး (0.519) သည် 0.05 ထက်မနည်းသောကြောင့်၊ ဖြေဆိုခဲ့သော ကြိုတင်ပြင်ဆင်စာမေးပွဲအရေအတွက်သည် စာမေးပွဲရလဒ်နှင့် စာရင်းအင်းအရ သိသာထင်ရှားသော ဆက်စပ်မှုရှိသည်ဟု ကျွန်ုပ်တို့ ကောက်ချက်မချနိုင်ပါ။

နောက်ဆုံးတွင်၊ ကျွန်ုပ်တို့သည် ကိန်းသေ ၊ နာရီ နှင့် prep_exams အတွက် ဇယားတွင်ပြထားသော တန်ဖိုးများကို အသုံးပြု၍ ဆုတ်ယုတ်မှုညီမျှခြင်းတစ်ခုကို ဖန်တီးနိုင်သည်။ ဤကိစ္စတွင်၊ ညီမျှခြင်းမှာ-

ခန့်မှန်းခြေ စာမေးပွဲရမှတ် = 67.674 + 5.556*(နာရီ) – 0.602*(prep_exams)

လေ့လာမှုနာရီအရေအတွက်နှင့် ၎င်းတို့ဖြေဆိုခဲ့သော လက်တွေ့စာမေးပွဲအရေအတွက်အပေါ် အခြေခံ၍ ကျောင်းသားတစ်ဦး၏ ခန့်မှန်းခြေ စာမေးပွဲရမှတ်ကို ရှာဖွေရန် ဤညီမျှခြင်းအား ကျွန်ုပ်တို့ အသုံးပြုနိုင်ပါသည်။ ဥပမာအားဖြင့်၊ ၃ နာရီစာလေ့လာပြီး ကြိုတင်ပြင်ဆင်မှု ၂ ကြိမ်ဖြေဆိုသော ကျောင်းသားသည် စာမေးပွဲရမှတ် 83.1 ရရှိသင့်သည်-

ခန့်မှန်းခြေ စာမေးပွဲရမှတ် = 67.674 + 5.556*(3) – 0.602*(2) = 83.1

မှတ်ချက်- ကြိုတင်ပြင်ဆင်မှုစာမေးပွဲများအတွက် ရှင်းလင်းချက်ကိန်းရှင်သည် ကိန်းဂဏန်းအရ သိသာထင်ရှားစွာမတွေ့သောကြောင့်၊ ၎င်းကို မော်ဒယ်မှဖယ်ရှားရန် ဆုံးဖြတ်ပြီး တစ်ခုတည်းသော ရှင်းပြချက်ကိန်းရှင်အဖြစ် လေ့လာထားသော နာရီများကို အသုံးပြု၍ ရိုးရှင်းသောမျဉ်းကြောင်းဆုတ်ယုတ်မှုကို လုပ်ဆောင်နိုင်သည်။