Spss တွင် ရိုးရှင်းသော linear regression လုပ်ဆောင်နည်း

Simple linear regression သည် ကြိုတင်ခန့်မှန်းကိန်းရှင်နှင့် တုံ့ပြန်မှုကိန်းရှင်ကြားရှိ ဆက်နွယ်မှုကို နားလည်ရန် ကျွန်ုပ်တို့အသုံးပြုနိုင်သည့် နည်းလမ်းတစ်ခုဖြစ်သည်။

ဤသင်ခန်းစာတွင် SPSS တွင် ရိုးရှင်းသောမျဉ်းကြောင်းပြန်ဆုတ်ခြင်းကို မည်သို့လုပ်ဆောင်ရမည်ကို ရှင်းပြထားသည်။

ဥပမာ- SPSS ရှိ ရိုးရှင်းသော မျဉ်းကြောင်းဆုတ်ယုတ်မှု

ကျွန်ုပ်တို့တွင် ကျောင်းသား 20 မှ ရရှိသော စာကျက်ချိန်နှင့် စာမေးပွဲအဆင့်ကို ပြသသည့် အောက်ပါဒေတာအတွဲရှိသည် ဆိုကြပါစို့။

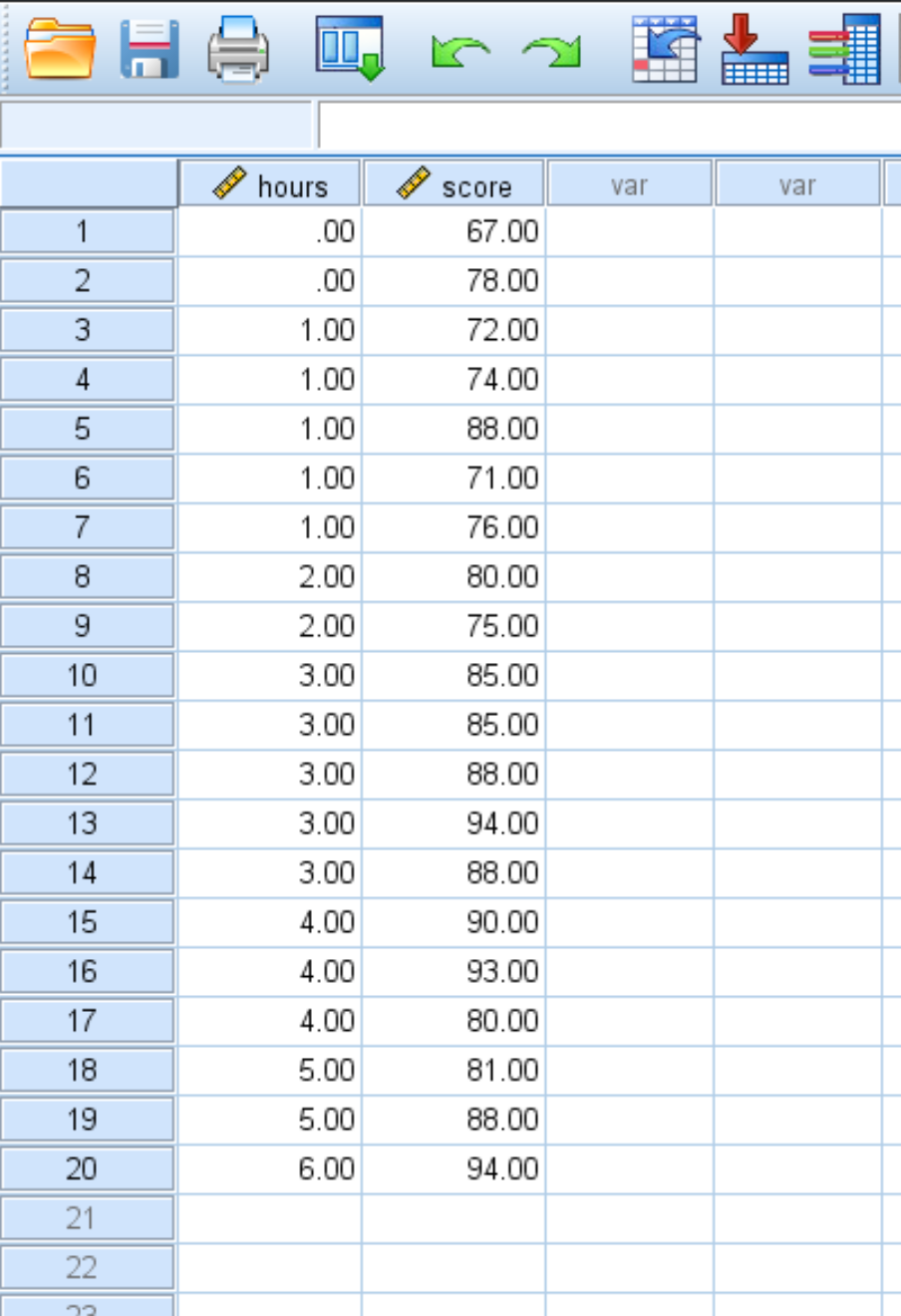
နာရီနှင့် စာမေးပွဲရမှတ်တို့ကြား ဆက်နွယ်မှုကို တွက်ချက်ရန် ဤဒေတာအတွဲတွင် ရိုးရှင်းသော မျဉ်းကြောင်းပြန်ဆုတ်ခြင်းကို လုပ်ဆောင်ရန် အောက်ပါအဆင့်များကို သုံးပါ-

အဆင့် 1- ဒေတာကို မြင်ယောင်ကြည့်ပါ။

ပထမဦးစွာ၊ ကိန်းရှင်နှစ်ခုကြားက မျဉ်းသားပုံပေါ်ကြောင်း သေချာစေရန် နာရီနှင့် ရမှတ်များကြား ဆက်စပ်မှုကို မြင်သာစေရန် အပိုင်းအစတစ်ခုကို ဖန်တီးပါမည်။ မဟုတ်ပါက၊ ရိုးရှင်းသော linear regression ကို အသုံးပြုရန် သင့်လျော်သော နည်းလမ်းတစ်ခု မဟုတ်ပေ။

Charts tab ကိုနှိပ်ပါ၊ ထို့နောက် Chart Builder ကိုနှိပ်ပါ။

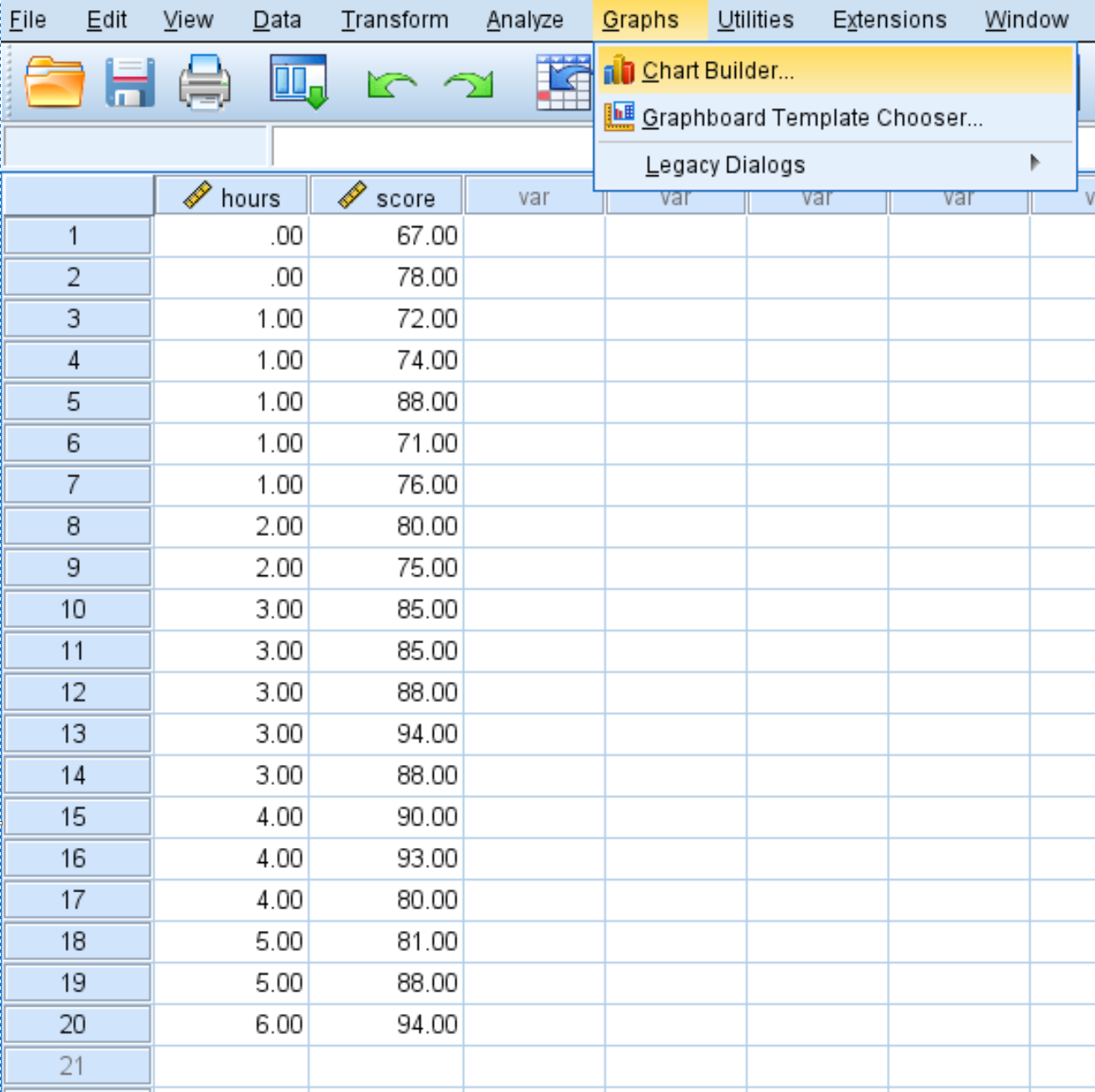
Choose From မီနူးမှ ပင်မတည်းဖြတ်ဝင်းဒိုးသို့ Scatter/Dot ကို နှိပ်ပြီး ဆွဲယူပါ။ ထို့နောက် ပြောင်းလဲနိုင်သော အကြိမ်များကို x-ဝင်ရိုးပေါ်သို့ ဆွဲတင်ကာ ရမှတ်ကို y-ဝင်ရိုးပေါ်သို့ ဆွဲတင်ပါ။

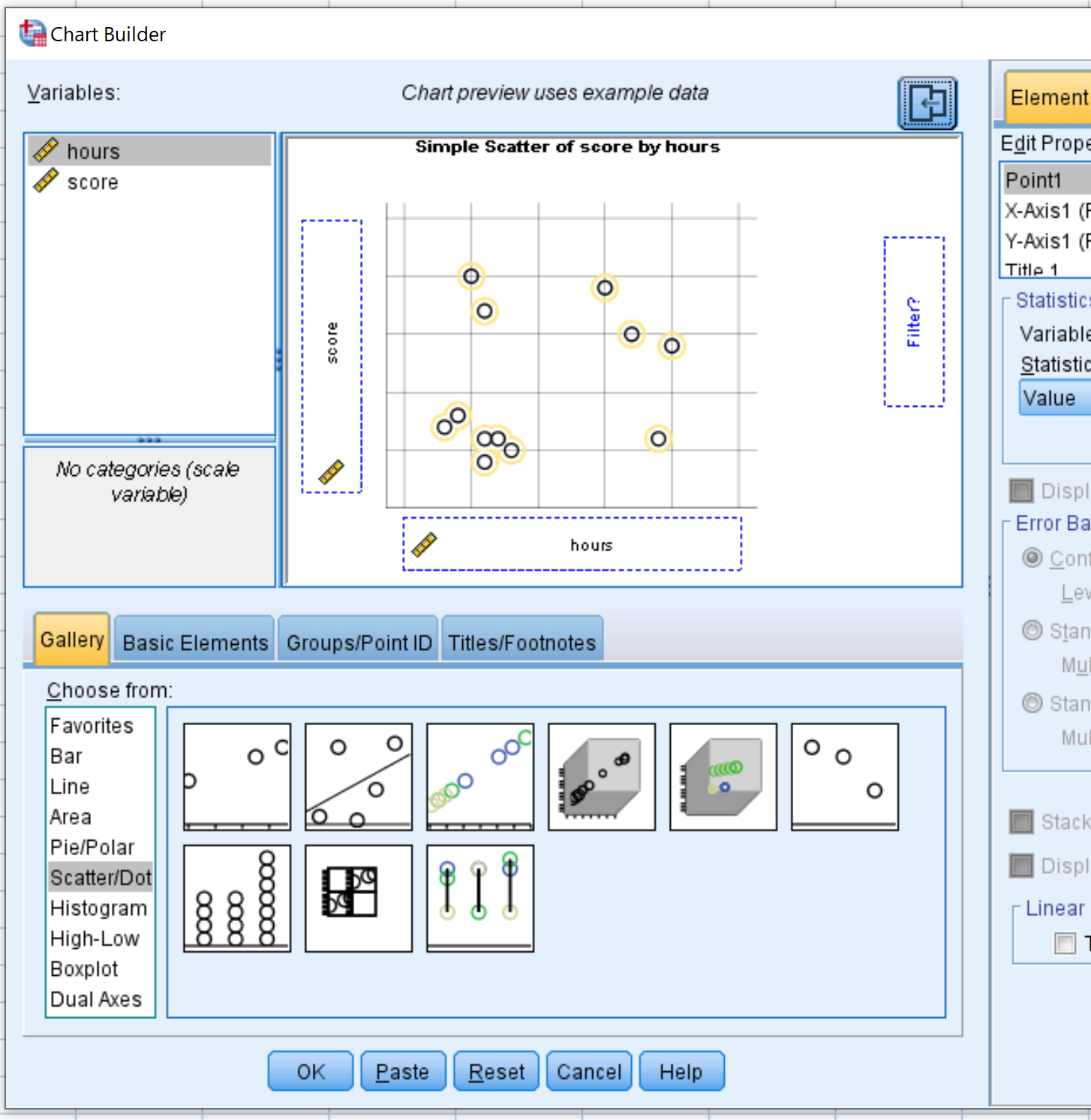
OK ကိုနှိပ်လိုက်သည်နှင့် အောက်ပါ scatter plot ပေါ်လာပါမည်။

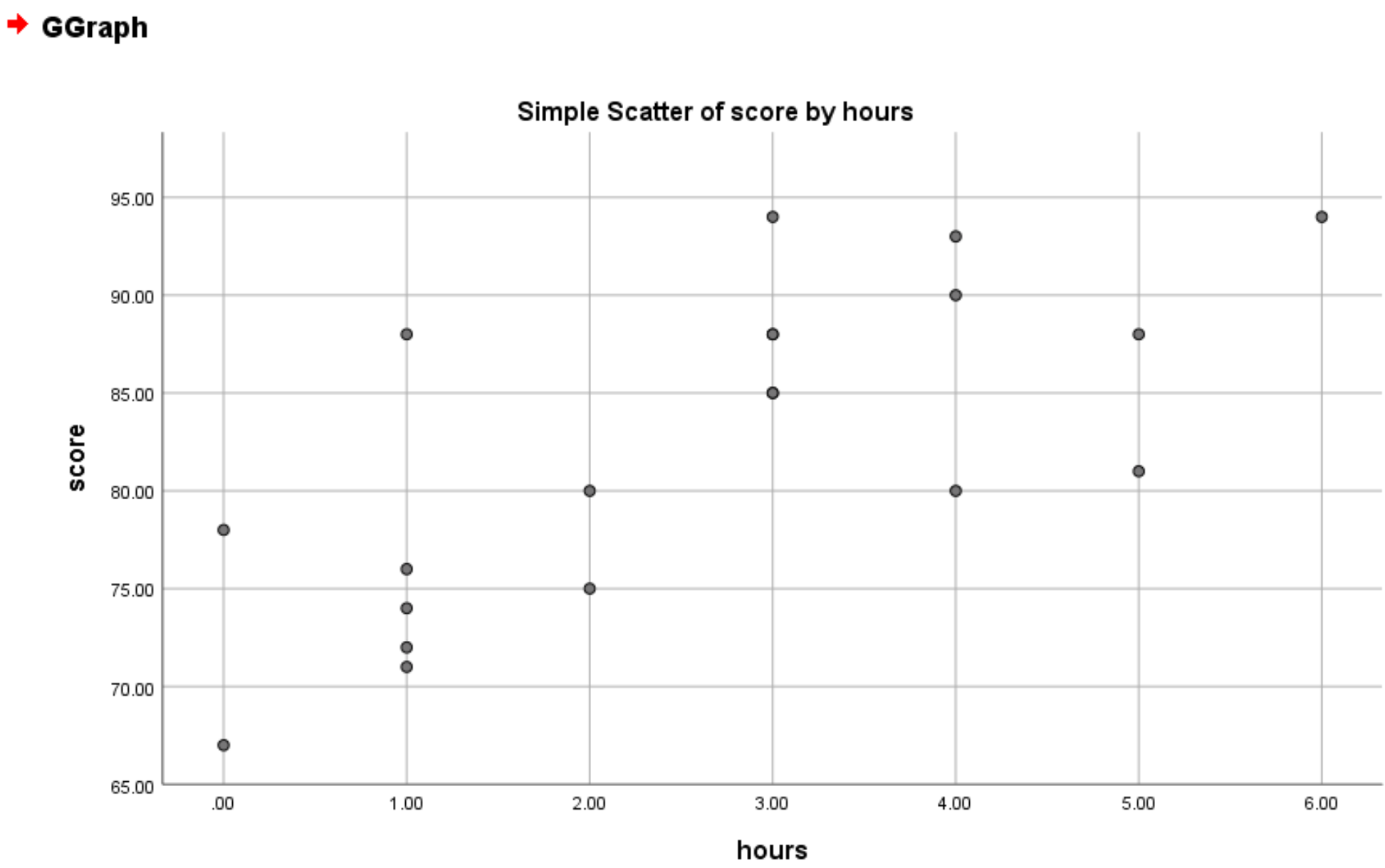
ဂရပ်မှ၊ နာရီနှင့် ရမှတ်ကြားတွင် အပြုသဘောဆောင်သော linear ဆက်နွယ်မှုရှိကြောင်း ကျွန်ုပ်တို့ တွေ့နိုင်ပါသည်။ ယေဘူယျအားဖြင့်၊ နာရီပိုလေ့လာသော ကျောင်းသားများသည် မြင့်မားသောရမှတ်များ ရှိသည်။

ကိန်းရှင်နှစ်ခုကြားတွင် ရှင်းလင်းပြတ်သားသော မျဉ်းသားဆက်နွယ်မှုရှိနေသောကြောင့်၊ ကျွန်ုပ်တို့သည် ရိုးရှင်းသောမျဉ်းဖြောင့်ဆုတ်ယုတ်မှုပုံစံကို ဒေတာအစုံနှင့် အံဝင်ခွင်ကျဖြစ်အောင် ဆက်လက်လုပ်ဆောင်သွားပါမည်။

အဆင့် 2- ရိုးရှင်းသော linear regression model ကို ကိုက်ညီပါ။

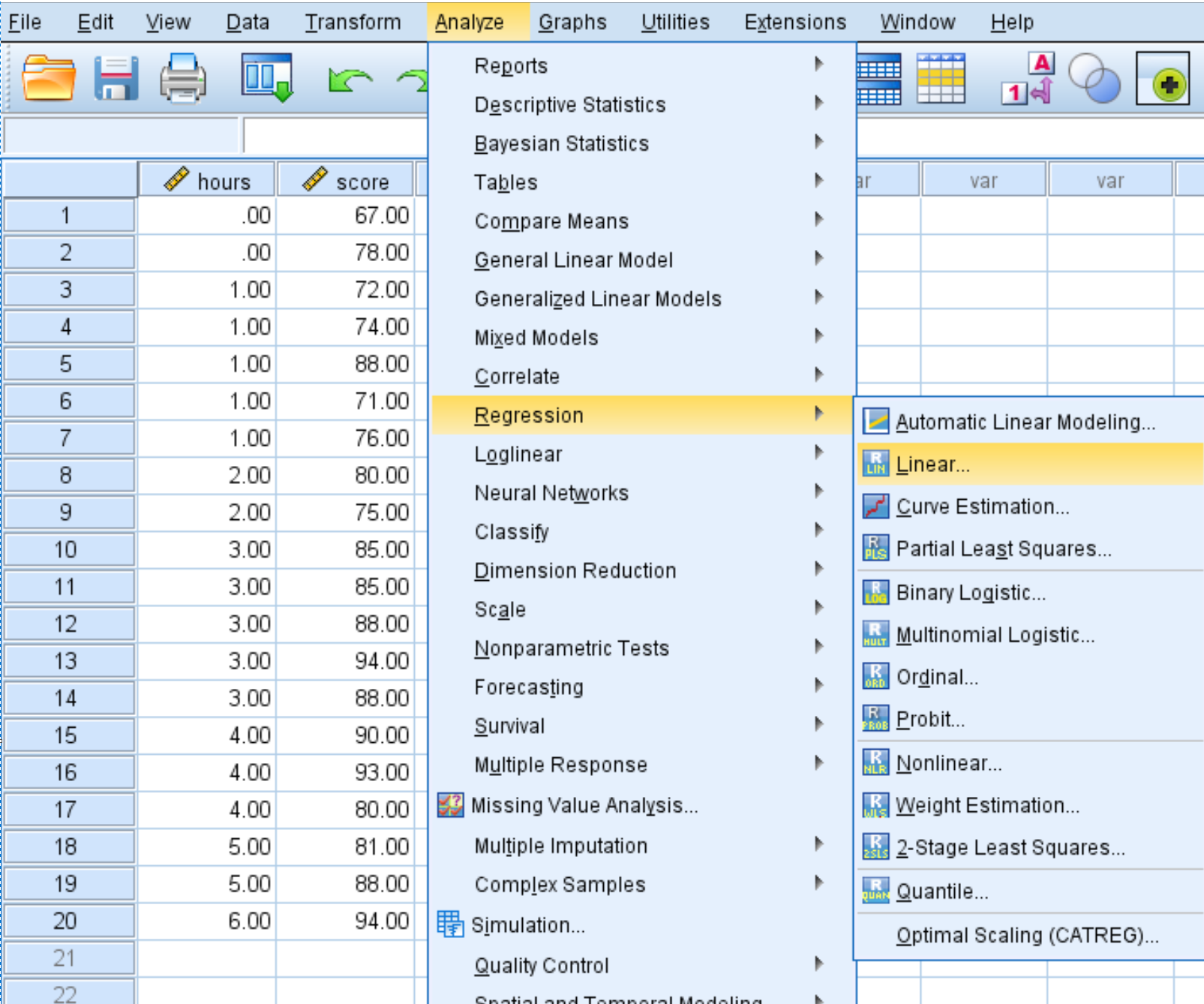
Analyze tab ကိုနှိပ်ပါ၊ ထို့နောက် Regression ၊ ထို့နောက် Linear :

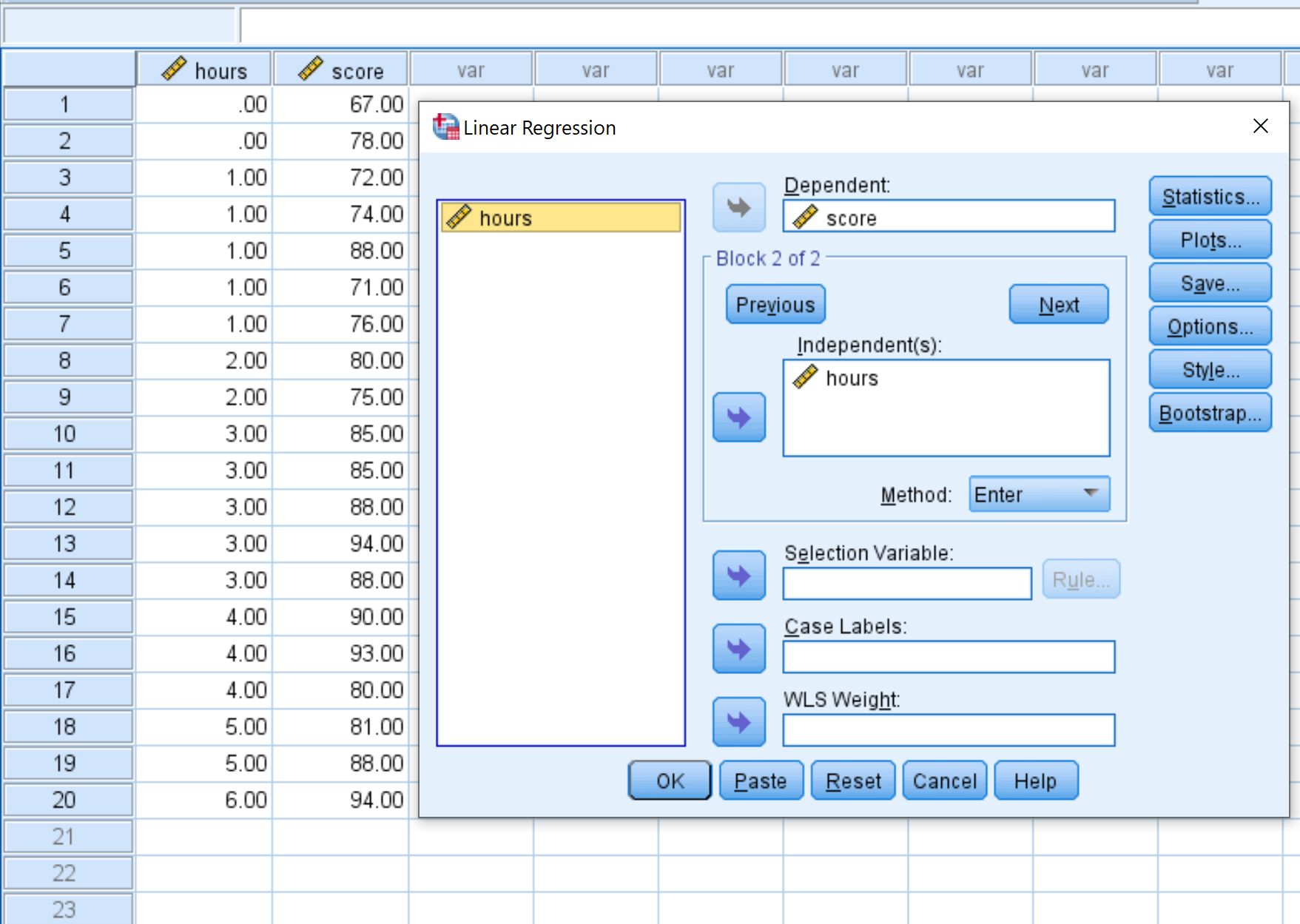
ပေါ်လာသည့် ဝင်းဒိုးအသစ်တွင်၊ မှီခိုမှုဟု တံဆိပ်တပ်ထားသော အကွက်ထဲသို့ ပြောင်းလဲနိုင်သော ရမှတ်ကို ဆွဲယူပြီး လွတ်လပ်သော တံဆိပ်တပ်ထားသော အကွက်ထဲသို့ နာရီများကို ဆွဲယူပါ။ ထို့နောက် OK ကိုနှိပ်ပါ။

အဆင့် 3- ရလဒ်များကို ဘာသာပြန်ပါ။

OK ကိုနှိပ်လိုက်သည်နှင့်၊ ရိုးရှင်းသော linear regression ရလဒ်များပေါ်လာလိမ့်မည်။ ကျွန်ုပ်တို့ စိတ်ဝင်စားသော ပထမဇယားမှာ မော်ဒယ် အကျဉ်းချုပ် ဖြစ်သည် ။

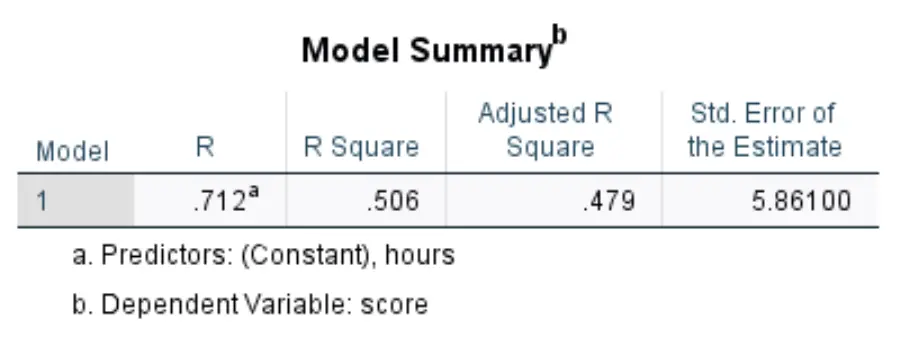
ဤဇယားရှိ အသက်ဆိုင်ဆုံးနံပါတ်များကို မည်သို့အဓိပ္ပာယ်ပြန်ဆိုရမည်ကို ဤတွင်ဖော်ပြထားသည်-

• R Square- ဤအရာသည် explanatory variable ဖြင့် ရှင်းပြနိုင်သော တုံ့ပြန်မှုကိန်းရှင်ရှိ ကွဲလွဲမှုအချိုးအစားဖြစ်သည်။ ဤဥပမာတွင်၊ စာမေးပွဲရမှတ်များ၏ ကွဲလွဲမှု 50.6% ကို နာရီများဖြင့် ရှင်းပြနိုင်သည်။
• စံ။ ခန့်မှန်းချက်အမှား- စံအမှား သည် သတိပြုမိသောတန်ဖိုးများနှင့် ဆုတ်ယုတ်မှုမျဉ်းကြားရှိ ပျမ်းမျှအကွာအဝေးဖြစ်သည်။ ဤဥပမာတွင်၊ လေ့လာတွေ့ရှိထားသောတန်ဖိုးများသည် ဆုတ်ယုတ်မှုမျဉ်းမှ ပျမ်းမျှယူနစ် 5,861 ဖြင့် သွေဖည်သွားပါသည်။

ကျွန်ုပ်တို့စိတ်ဝင်စားသော အောက်ပါဇယားသည် Coefficients ခေါင်းစဉ်ဖြစ်သည်။

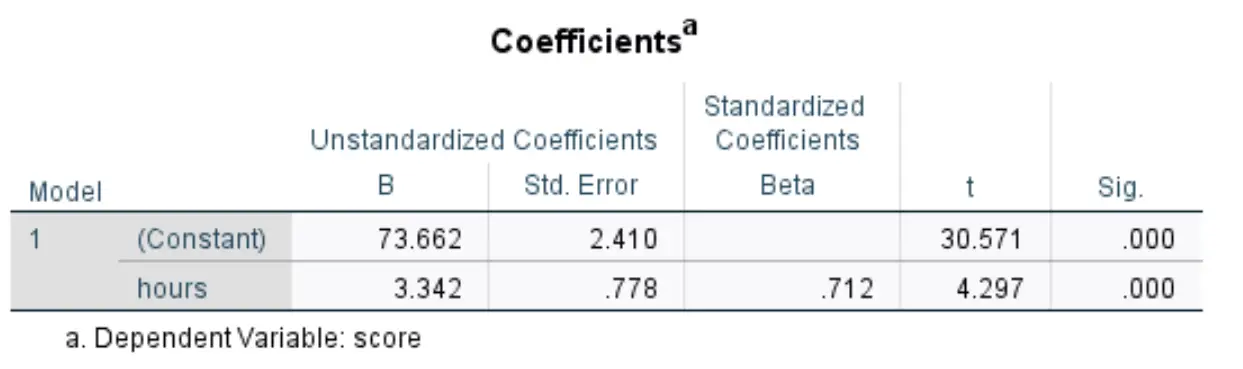
ဤဇယားရှိ အသက်ဆိုင်ဆုံးနံပါတ်များကို မည်သို့အဓိပ္ပာယ်ပြန်ဆိုရမည်ကို ဤတွင်ဖော်ပြထားသည်-

• Unstandardized B (Constant) : ကြိုတင်ခန့်မှန်းကိန်းရှင်သည် သုညဖြစ်သောအခါ ၎င်းသည် တုံ့ပြန်မှုကိန်းရှင် ၏ ပျမ်းမျှတန်ဖိုးကို ပြောပြသည်။ ဤဥပမာတွင်၊ လေ့လာသည့်နာရီသည် သုညဖြစ်ပြီး ပျမ်းမျှ စာမေးပွဲရမှတ်မှာ 73.662 ဖြစ်သည်။
• B စံချိန်စံညွှန်းမမီသော (နာရီများ)- ၎င်းသည် ခန့်မှန်းသူကိန်းရှင်၏ တစ်ယူနစ်တိုးလာမှုနှင့်ဆက်စပ်နေသော တုံ့ပြန်မှုကိန်းရှင်၏ ပျမ်းမျှပြောင်းလဲမှုကို ပြောပြသည်။ ဤဥပမာတွင်၊ လေ့လာမှုတစ်ခုစီသည် ပျမ်းမျှအားဖြင့် စာမေးပွဲရမှတ် 3,342 တိုးခြင်းနှင့် ဆက်စပ်နေသည်။
• Sig (နာရီ)- ၎င်းသည် နာရီပိုင်းအတွင်း စမ်းသပ်စာရင်းအင်းနှင့် ဆက်စပ်နေသည့် p-တန်ဖိုး ဖြစ်သည်။ ဤကိစ္စတွင်၊ ဤတန်ဖိုးသည် 0.05 ထက်နည်းသောကြောင့်၊ ကြိုတင်ခန့်မှန်းနိုင်သော ပြောင်းလဲနိုင်သော နာရီများသည် စာရင်းအင်းအရ သိသာထင်ရှားသည်ဟု ကျွန်ုပ်တို့ ကောက်ချက်ချနိုင်ပါသည်။

နောက်ဆုံးတွင်၊ ကျွန်ုပ်တို့သည် ကိန်းသေ နှင့် နာရီ တန်ဖိုးများကို အသုံးပြု၍ ဆုတ်ယုတ်မှုညီမျှခြင်းကို ဖွဲ့နိုင်သည်။ ဤကိစ္စတွင်၊ ညီမျှခြင်းမှာ-

ခန့်မှန်းခြေ စာမေးပွဲရမှတ် = 73.662 + 3.342*(နာရီ)

လေ့လာခဲ့သည့် နာရီအရေအတွက်ပေါ်အခြေခံ၍ ကျောင်းသားတစ်ဦး၏ ခန့်မှန်းခြေ စာမေးပွဲရမှတ်ကို ရှာဖွေရန် ဤညီမျှခြင်းအား ကျွန်ုပ်တို့ အသုံးပြုနိုင်ပါသည်။

ဥပမာအားဖြင့်၊ ၃ နာရီကြာလေ့လာသော ကျောင်းသားသည် စာမေးပွဲရမှတ် 83.688 ရရှိသင့်သည်-

ခန့်မှန်းစာမေးပွဲရမှတ် = 73.662 + 3.342*(3) = 83.688

အဆင့် 4- ရလဒ်များကို သတင်းပို့ပါ။

နောက်ဆုံးတွင်၊ ကျွန်ုပ်တို့သည် ကျွန်ုပ်တို့၏ရိုးရှင်းသော မျဉ်းဖြောင့်ဆုတ်ယုတ်မှု၏ရလဒ်များကို အကျဉ်းချုပ်တင်ပြလိုပါသည်။ ဤသည်မှာ ဤအရာကို ပြုလုပ်ပုံ၏ ဥပမာတစ်ခုဖြစ်သည်။

လေ့လာမှုနာရီနှင့် စာမေးပွဲအဆင့်ကြား ဆက်နွယ်မှုကို တွက်ချက်ရန် ရိုးရှင်းသော မျဉ်းတန်းဆုတ်ယုတ်မှုကို လုပ်ဆောင်ခဲ့သည်။ ခွဲခြမ်းစိတ်ဖြာမှုတွင် ကျောင်းသား ၂၀ ၏ နမူနာကို အသုံးပြုခဲ့သည်။

ရလဒ်များက လေ့လာမှုနာရီနှင့် စာမေးပွဲအဆင့် (t = 4.297, p < 0.000) အကြား ကိန်းဂဏန်းအချက်အလတ် သိသိသာသာ ဆက်စပ်မှုရှိသည်ကို ပြသခဲ့ပြီး ထိုနာရီများသည် စာမေးပွဲအဆင့်တွင် ရှင်းပြထားသော ကွဲလွဲမှု၏ 50.6% ဖြစ်သည်။ စာမေးပွဲ။

ဆုတ်ယုတ်မှုညီမျှခြင်းမှာ-

ခန့်မှန်းခြေ စာမေးပွဲရမှတ် = 73.662 + 3.342*(နာရီ)

လေ့လာမှုတစ်ခုစီသည် ပျမ်းမျှအားဖြင့် စာမေးပွဲရမှတ် 3,342 တိုးလာခြင်းနှင့် ဆက်စပ်နေသည်။

ထပ်လောင်းအရင်းအမြစ်များ

အောက်ဖော်ပြပါ သင်ခန်းစာများသည် SPSS တွင် အခြားဘုံအလုပ်များကို မည်သို့လုပ်ဆောင်ရမည်ကို ရှင်းပြသည်-

SPSS တွင် မျဉ်းကြောင်းပြန်ဆုတ်မှု အများအပြားကို မည်သို့လုပ်ဆောင်ရမည်နည်း။
SPSS တွင် လေးပုံတပုံ ဆုတ်ယုတ်မှုအား မည်သို့လုပ်ဆောင်ရမည်နည်း။
SPSS တွင် logistic regression လုပ်နည်း