Spss တွင် roc curve ကိုဖန်တီးပြီးအဓိပ္ပာယ်ဖွင့်နည်း

Logistic regression သည် response variable binary ဖြစ်သောအခါ regression model တစ်ခုနှင့် ကိုက်ညီရန် ကျွန်ုပ်တို့အသုံးပြုသည့် ကိန်းဂဏန်းဆိုင်ရာ နည်းလမ်းတစ်ခုဖြစ်သည်။ ထောက်ပံ့ပို့ဆောင်ရေး ဆုတ်ယုတ်မှုပုံစံသည် ဒေတာအစုံနှင့် မည်မျှကိုက်ညီကြောင်း အကဲဖြတ်ရန်၊ အောက်ပါ မက်ထရစ်နှစ်ခုကို ကြည့်နိုင်သည်-

• အာရုံခံစားနိုင်မှု- ရလဒ်အမှန်တကယ်အပြုသဘောဆောင်သောအခါတွင် လေ့လာမှုတစ်ခုအတွက် အပြုသဘောဆောင်သောရလဒ်ကို မော်ဒယ်က ခန့်မှန်းပေးသည့်ဖြစ်နိုင်ခြေ။
• တိကျမှု- ရလဒ်အမှန်တကယ် အနုတ်လက္ခဏာဖြစ်သောအခါ စောင့်ကြည့်မှုတစ်ခုအတွက် အနုတ်ရလဒ်ကို မော်ဒယ်က ခန့်မှန်းသည့် ဖြစ်နိုင်ခြေ။

ဤမက်ထရစ်နှစ်ခုကို မြင်သာစေရန် ရိုးရှင်းသောနည်းလမ်းမှာ ထောက်ပံ့ပို့ဆောင်ရေး ဆုတ်ယုတ်မှုပုံစံ၏ အာရုံခံနိုင်စွမ်းနှင့် တိကျမှုကိုပြသသည့် ဂရပ်တစ်ခုဖြစ်သည့် ROC မျဉ်းကွေးကို ဖန်တီးရန်ဖြစ်သည်။

ဤသင်ခန်းစာသည် SPSS တွင် ROC မျဉ်းကွေးတစ်ခုကို ဖန်တီးပြီး အဓိပ္ပာယ်ပြန်ဆိုနည်းကို ရှင်းပြထားသည်။

ဥပမာ- SPSS ရှိ ROC မျဉ်းကွေး

ကျွန်ုပ်တို့တွင် ဘတ်စကက်ဘောကစားသမားတစ်ဦးအား NBA (0 = မဟုတ်ဘူး၊ 1 = yes) နှင့် ကောလိပ်ရှိ ဂိမ်းပျမ်းမျှအလိုက် ရမှတ်များအလိုက် ဘတ်စကက်ဘောကစားသမားတစ်ဦးကို ရေးဆွဲထားခြင်း ရှိ၊ မရှိကို ပြသသည့် အောက်ပါဒေတာအစုံရှိသည် ဆိုကြပါစို့။

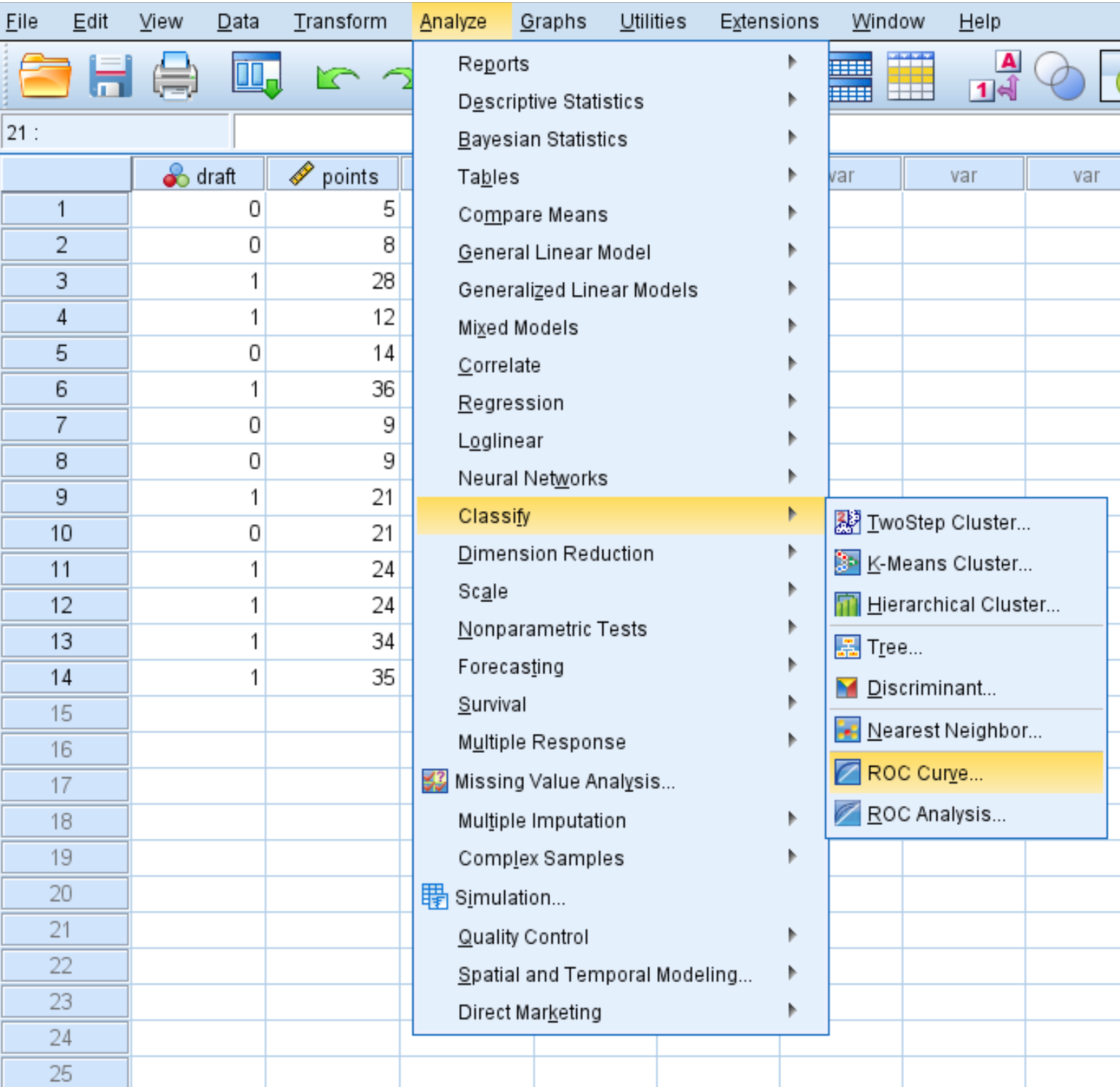
ဤဒေတာအတွဲအတွက် ROC မျဉ်းကွေးကို ဖန်တီးရန်၊ ခွဲခြမ်းစိတ်ဖြာခြင်း tab ကို နှိပ်ပါ၊ ထို့နောက် Classify ၊ ထို့နောက် ROC Curve :

ပေါ်လာသည့် ဝင်းဒိုးအသစ်တွင်၊ State Variable တံဆိပ်တပ်ထားသော ဧရိယာထဲသို့ မူကြမ်းကို ဆွဲယူပါ။ state variable ၏တန်ဖိုးကို 1 သို့သတ်မှတ်ပါ။ (ဤသည်မှာ ကစားသမားတစ်ဦးကို ရေးဆွဲထားသည်ကို ညွှန်ပြသော တန်ဖိုးဖြစ်သည်)။ Test Variable ဟုအမည်တပ်ထားသော ဧရိယာထဲသို့ ပြောင်းလဲနိုင်သော အမှတ်များကို ဆွဲယူပါ။

ထောင့်ဖြတ်အကိုးအကားလိုင်း နှင့် ROC မျဉ်းကွေးအမှတ် သြဒိနိတ်များ နှင့်အတူ ဘေးရှိ အကွက်များကို စစ်ဆေးပါ။ ထို့နောက် OK ကိုနှိပ်ပါ။

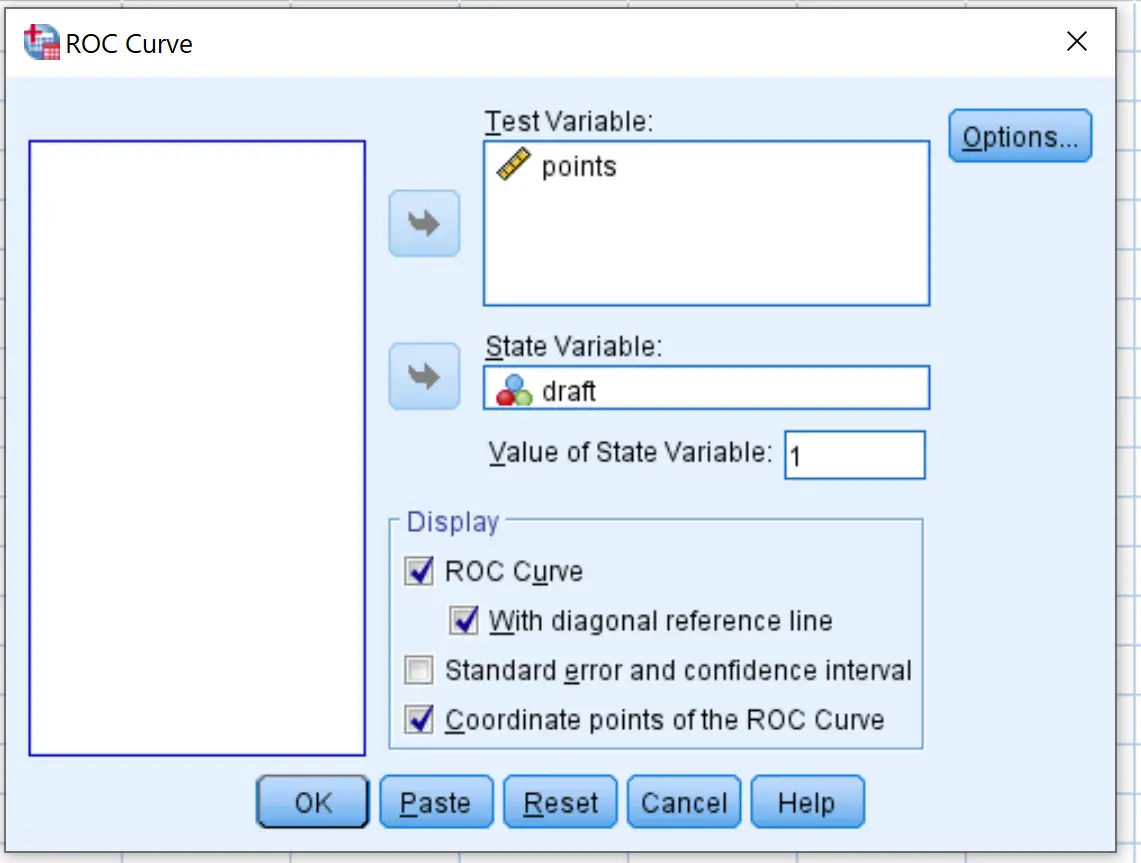
ဤသည်မှာ ရလဒ်ကို မည်သို့အဓိပ္ပာယ်ဖွင့်ဆိုနိုင်သည်-

ဖိုင်လုပ်ဆောင်ခြင်း၏ အကျဉ်းချုပ်-

ဤဇယားသည် ဒေတာအတွဲရှိ အပြုသဘောနှင့် အနုတ်လက္ခဏာကိစ္စများ စုစုပေါင်းအရေအတွက်ကို ပြသသည်။ ဤဥပမာတွင် ကစားသမား 8 ဦးကို ရေးဆွဲထားပြီး (အပြုသဘောဆောင်သောရလဒ်) နှင့် ကစားသမား 6 ဦးကို ရေးဆွဲထားခြင်းမဟုတ်ပါ (အနုတ်လက္ခဏာရလဒ်)။

ROC မျဉ်းကွေး-

လက်ခံသူ၏လည်ပတ်မှုလက္ခဏာရပ် (ROC) မျဉ်းကွေးသည် 0 မှ 1 သို့ပြောင်းလဲသွားသောကြောင့် တံခါးခုံတန်ဖိုးသည် 0 မှ 1 သို့ပြောင်းလဲသွားသောကြောင့် အာရုံခံနိုင်စွမ်းတန်ဖိုးများနှင့် တိကျသေချာမှု 1 နှင့် ကွက်ကွက်တစ်ခုဖြစ်သည်။

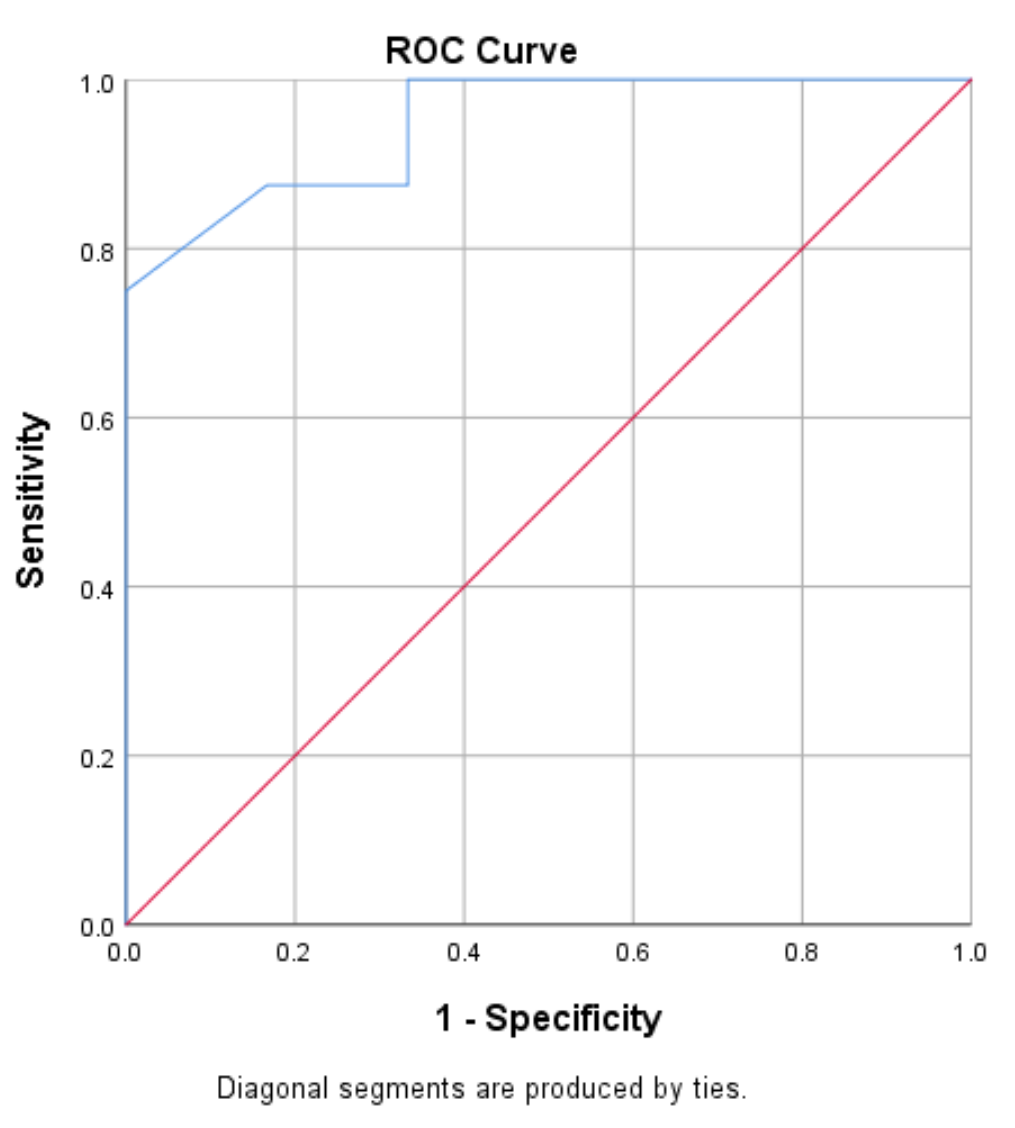
အာရုံခံနိုင်စွမ်းနှင့် တိကျမှုမြင့်မားသော မော်ဒယ်တွင် ကွက်ကွက်၏ ဘယ်ဘက်အပေါ်ထောင့်နှင့် ကိုက်ညီသော ROC မျဉ်းကွေးတစ်ခု ရှိပါမည်။ အာရုံခံနိုင်စွမ်းနည်းပြီး တိကျမှုနည်းသော မော်ဒယ်သည် 45 ဒီဂရီ ထောင့်ဖြတ်အနီးကပ် မျဉ်းကွေးတစ်ခု ရှိပါမည်။

ဤဥပမာရှိ ROC မျဉ်းကွေး (အပြာရောင်မျဉ်း) သည် ကွက်ကွက်၏ ဘယ်ဘက်အပေါ်ထောင့်ကို ပွေ့ဖက်ထားပြီး မော်ဒယ်သည် ကစားသူများ၏ ပျမ်းမျှရမှတ်များပေါ် မူတည်၍ ဂိမ်းတစ်ခုလျှင် ၎င်းတို့၏ ပျမ်းမျှရမှတ်များပေါ် မူတည်၍ ရေးဆွဲခြင်းရှိ၊ . .

မျဉ်းကွေးအောက်ရှိ ဧရိယာ

မျဉ်းကွေးအောက်ရှိ ဧရိယာသည် ကျွန်ုပ်တို့အား မော်ဒယ်၏ အပြုသဘောနှင့် အနုတ်ရလဒ်များကြား ပိုင်းခြားနိုင်စွမ်းကို အကြံဥာဏ်ပေးသည်။ AUC သည် 0 မှ 1 အထိ ကွာဟနိုင်သည်။ AUC မြင့်မားလေ၊ မော်ဒယ်သည် ရလဒ်များကို မှန်ကန်စွာ ခွဲခြားနိုင်လေလေဖြစ်သည်။

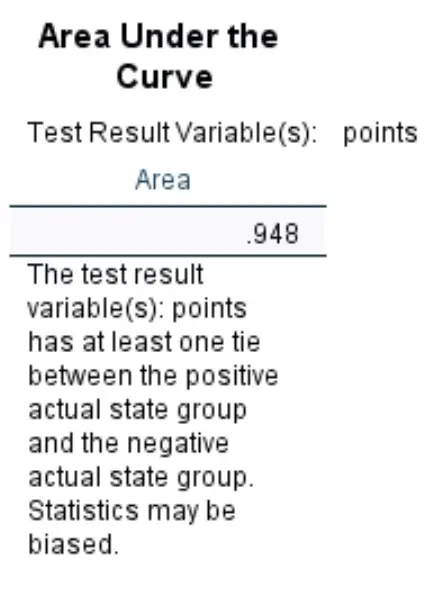
ဤအထူးကုန်စည်ပို့ဆောင်မှုဆုတ်ယုတ်မှုပုံစံအတွက် AUC သည် 0.948 ဖြစ်ပြီး အလွန်မြင့်မားသည်ကို ကျွန်ုပ်တို့တွေ့မြင်နိုင်ပါသည်။ ၎င်းသည် ကစားသမားတစ်ဦးကို ရေးဆွဲမည် သို့မဟုတ် မရေးဆွဲမည်ကို ကြိုတင်ခန့်မှန်းရန် မော်ဒယ်သည် ကောင်းမွန်စွာလုပ်ဆောင်ကြောင်း ဖော်ပြသည်။

မျဉ်းကွေး၏ ညှိနှိုင်းချက်များ

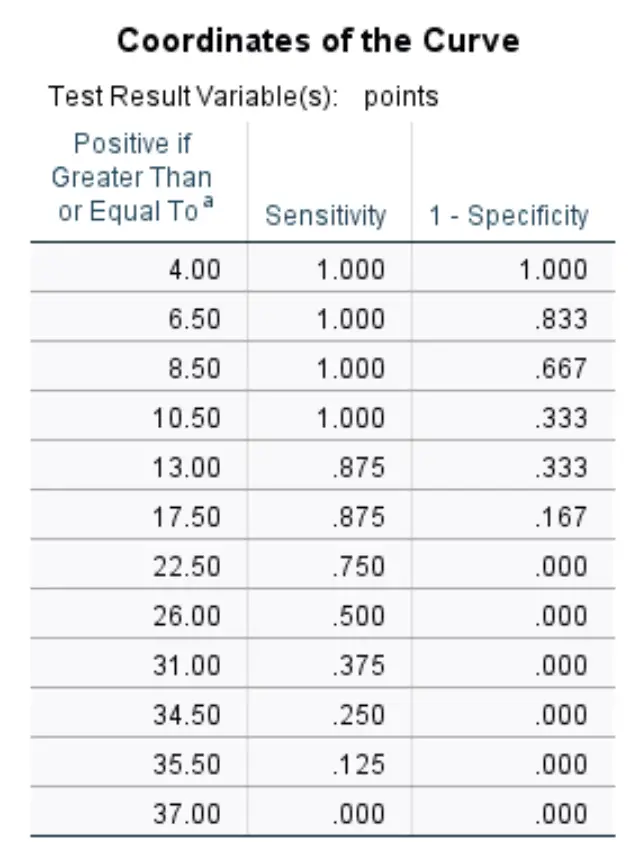
ဤနောက်ဆုံးဇယားသည် မတူညီသောအဆင့်များအတွက် ROC မျဉ်းကွေး၏ sensitivity နှင့် specificity 1 ကိုပြသသည်။

ဥပမာအားဖြင့်:

ကျွန်ုပ်တို့သည် အဆင့်သတ်မှတ်ချက် 8.50 ဖြစ်ခွင့်ပြုပါက၊ ဆိုလိုသည်မှာ ဂိမ်းတစ်ခုလျှင် ရမှတ် 8.50 ထက်နည်းသော ကစားသမားတိုင်းကို မူကြမ်းရေးဆွဲမည်မဟုတ်ကြောင်းနှင့် ဂိမ်းတစ်ခုလျှင် ရမှတ် 8.50 ထက်ပိုသော ကစားသမားများကို ရေးဆွဲပေးမည်ဟု ကျွန်ုပ်တို့ မျှော်လင့်ပါသည်။

၎င်းကို သတ်မှတ်ချက်တစ်ခုအဖြစ် အသုံးပြုခြင်းဖြင့် ကျွန်ုပ်တို့၏ အာရုံခံနိုင်စွမ်း သည် 100% (ဂိမ်းတစ်ခုလျှင် 8.50 မှတ်ထက်နည်းသော ကစားသမားတိုင်းကို အမှန်ပင် မရေးဆွဲထားသောကြောင့်) နှင့် ကျွန်ုပ်တို့၏ တိကျမှု 1 သည် 66.7% ဖြစ်မည် (12 မှတ်ထက် 8.50 မှတ်ထက်ပိုသော ကစားသမား 8 ဦးမှ 8 ဦး ဖြစ်သောကြောင့် ဂိမ်းတစ်ခုစီကို ရေးဆွဲခဲ့သည်။)

အထက်ဖော်ပြပါဇယားသည် ဖြစ်နိုင်ချေအဆင့်တစ်ခုစီအတွက် အာရုံခံနိုင်စွမ်းနှင့် တိကျမှု 1 ကို မြင်နိုင်စေပါသည်။