Sum of squares အတွက် နူးညံ့သောလမ်းညွှန်ချက်- sst၊ ssr၊ sse

Linear regression ကို data အစုအဝေး “ ကိုက်ညီ” အသင့်တော်ဆုံးမျဉ်းကိုရှာရန်အသုံးပြုသည်။

ဆုတ်ယုတ်မှုမျဉ်းသည် ဒေတာနှင့် အမှန်တကယ်ကိုက်ညီမှုရှိမရှိကို တိုင်းတာရန် မတူညီသော လေးထောင့် တန်ဖိုးသုံးခုကို အသုံးပြုလေ့ရှိသည်-

1. စုစုပေါင်းစတုရန်းများ (SST) – တစ်ဦးချင်းဒေတာအချက်များ (y _i ) နှင့် တုံ့ပြန်မှုကိန်းရှင်၏ပျမ်းမျှ ( y ) အကြား ကွာခြားချက်များ၏ လေးထပ်ကိန်းများ။

• SST = Σ(y _i – y ) ^၂

2. Sum of Squares Regression (SSR) – ခန့်မှန်းထားသော ဒေတာအချက်များ (ŷ _i ) နှင့် တုံ့ပြန်မှု variable ၏ပျမ်းမျှ ( y ) အကြားကွာခြားချက်များ၏ နှစ်ထပ်ကိန်းများ။

• SSR = Σ(ŷ _i – y ) ^၂

3. Sum of Squares Error (SSE) – ခန့်မှန်းထားသော ဒေတာအချက်များ (ŷ _i ) နှင့် စောင့်ကြည့်လေ့လာထားသော ဒေတာအချက်များ (y _i ) အကြား ကွာခြားချက်များ၏ လေးထပ်ကိန်းများ။

• SSE = Σ(ŷ _i – y _i ) ^၂

ဤအစီအမံသုံးခုကြားတွင် အောက်ပါ ဆက်စပ်မှု ရှိပါသည်။

SST = SSR + SSE

ထို့ကြောင့် ဤတိုင်းတာမှုနှစ်ခုကို ကျွန်ုပ်တို့သိပါက တတိယမြောက်ကို တွက်ချက်ရန် ရိုးရှင်းသော အက္ခရာသင်္ချာကို အသုံးပြုနိုင်သည်။

SSR၊ SST နှင့် R-Square

R-squared သည် တစ်ခါတစ်ရံတွင် ဆုံးဖြတ်ခြင်း၏ coefficient ဟုခေါ်သည်၊ သည် linear regression model တစ်ခုသည် data set တစ်ခုနှင့် မည်မျှ အံဝင်ခွင်ကျဖြစ်သနည်းဟူသည့် အတိုင်းအတာတစ်ခုဖြစ်သည်။ ခန့်မှန်းသူကိန်းရှင်က ရှင်းပြနိုင်သည့် တုံ့ပြန်မှုကိန်း ရှင်ရှိ ကွဲလွဲမှု၏ အချိုးအစားကို ကိုယ်စားပြုသည်။

R-squared တန်ဖိုးသည် 0 မှ 1 အထိ ကွာဟနိုင်သည်။ 0 တန်ဖိုးသည် ခန့်မှန်းသူကိန်းရှင်က လုံးဝရှင်းပြမရနိုင်သော တုံ့ပြန်မှုကိန်းရှင်ကို ညွှန်ပြသည်။ 1 ၏တန်ဖိုးသည် တုံ့ပြန်မှုကိန်းရှင်အား ကြိုတင်ခန့်မှန်းကိန်းရှင်မှ အမှားအယွင်းမရှိဘဲ စုံလင်စွာရှင်းပြနိုင်သည်ကို ညွှန်ပြသည်။

SSR နှင့် SST ကိုအသုံးပြု၍ R နှစ်ထပ်ကိန်းကို အောက်ပါအတိုင်း တွက်ချက်နိုင်ပါသည်။

R နှစ်ထပ်ကိန်း = SSR/SST

ဥပမာအားဖြင့်၊ ပေးထားသော regression model အတွက် SSR သည် 137.5 ဖြစ်ပြီး SST သည် 156 ဖြစ်ပါက၊ R နှစ်ထပ်ကိန်းကို အောက်ပါအတိုင်း တွက်ချက်ပါမည်-

R နှစ်ထပ် = 137.5 / 156 = 0.8814

တုံ့ပြန်မှုကိန်းရှင်တွင် ကွဲလွဲမှု 88.14% ကို ကြိုတင်ခန့်မှန်းကိန်းရှင်က ရှင်းပြနိုင်သည်ဟု ၎င်းကဆိုသည်။

SST၊ SSR၊ SSE တွက်ချက်ပါ- အဆင့်ဆင့် ဥပမာ

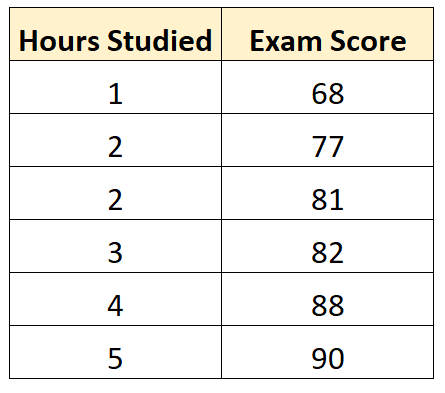
ကျွန်ုပ်တို့တွင် မတူညီသောကျောင်းသားခြောက်ဦးမှ ဖြေဆိုခဲ့သည့် နောက်ဆုံးစာမေးပွဲရမှတ်များနှင့်အတူ အောက်ပါဒေတာအစုံရှိသည်ဆိုပါစို့။

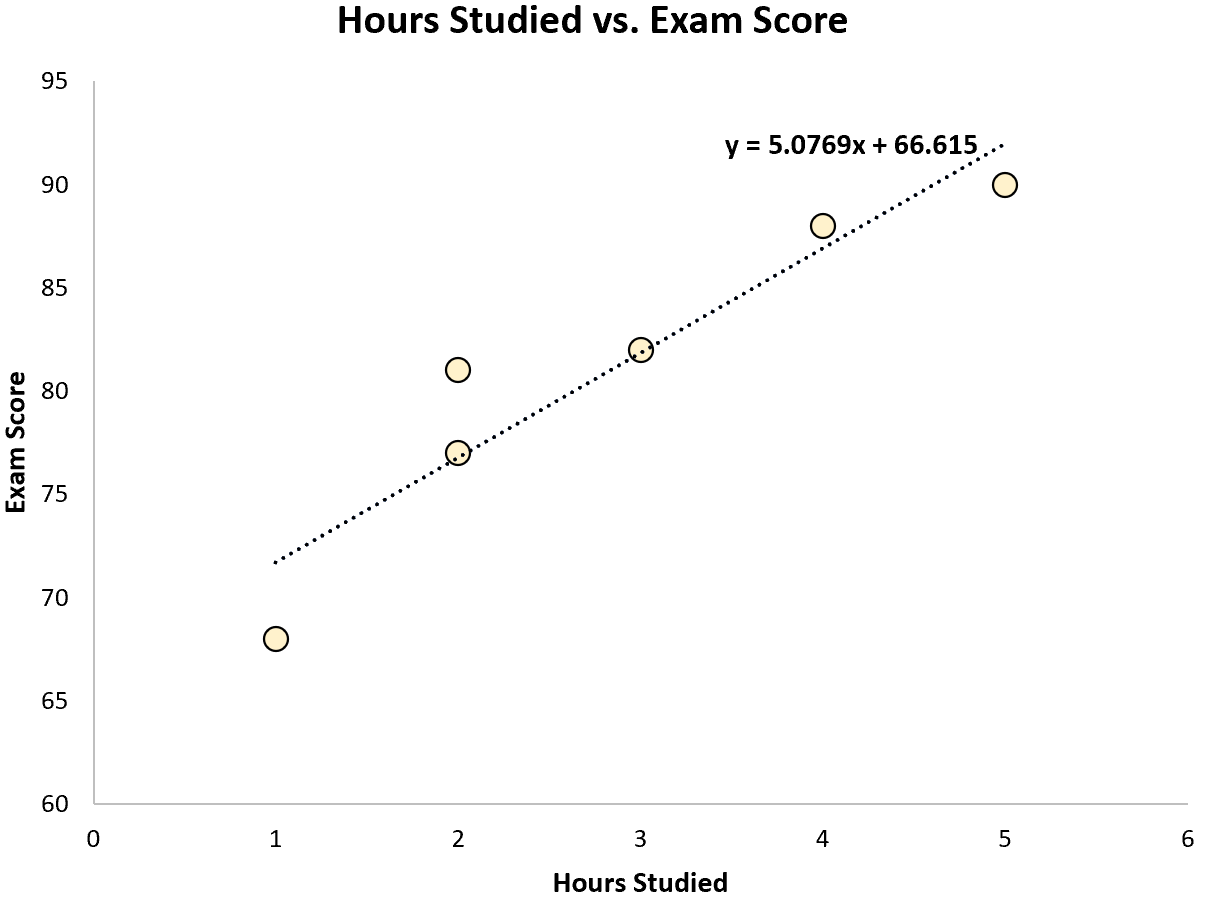
အချို့သော စာရင်းအင်းဆော့ဖ်ဝဲများ ( R ၊ Excel ၊ Python ကဲ့သို့ ) သို့မဟုတ် လက်ဖြင့်ပင် အသုံးပြုခြင်းဖြင့် အကောင်းဆုံး-အံဝင်ခွင်ကျ မျဉ်းကြောင်းကို ကျွန်ုပ်တို့တွေ့မြင်နိုင်သည်-

ရမှတ် = 66.615 + 5.0769*(နာရီ)

အသင့်တော်ဆုံးညီမျှခြင်းမျဉ်းကို ကျွန်ုပ်တို့သိသည်နှင့် SST၊ SSR နှင့် SSE တို့ကို တွက်ချက်ရန် အောက်ပါအဆင့်များကို အသုံးပြုနိုင်ပါသည်။

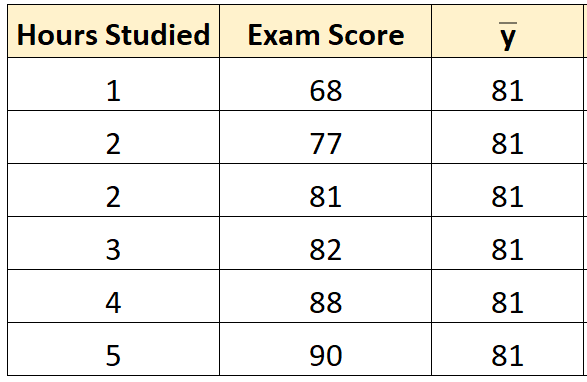
အဆင့် 1- တုံ့ပြန်မှုကိန်းရှင်၏ ပျမ်းမျှအား တွက်ချက်ပါ။

တုံ့ပြန်မှုကိန်းရှင်၏ပျမ်းမျှ ( y ) သည် 81 ဖြစ်လာသည်။

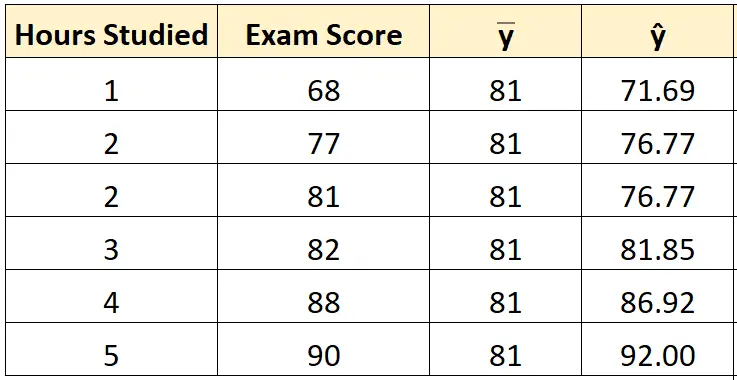
အဆင့် 2- စောင့်ကြည့်မှုတစ်ခုစီအတွက် ခန့်မှန်းတန်ဖိုးကို တွက်ချက်ပါ။

ထို့နောက် ကျောင်းသားတစ်ဦးစီအတွက် ကြိုတင်ခန့်မှန်းထားသော စာမေးပွဲရမှတ် () ကို တွက်ချက်ရန် အသင့်တော်ဆုံး ညီမျှခြင်းမျဉ်းကို ကျွန်ုပ်တို့ အသုံးပြုနိုင်ပါသည်။

ဥပမာအားဖြင့်၊ တစ်နာရီလေ့လာသော ကျောင်းသားအတွက် ခန့်မှန်းထားသော စာမေးပွဲအဆင့်မှာ-

ရမှတ် = 66.615 + 5.0769*(1) = 71.69 ။

ကျောင်းသားတစ်ဦးစီအတွက် ခန့်မှန်းရမှတ်ကို ရှာဖွေရန် တူညီသောချဉ်းကပ်နည်းကို အသုံးပြုနိုင်ပါသည်။

အဆင့် 3- စုစုပေါင်းစတုရန်းများ (SST) ကို တွက်ချက်ပါ။

ထို့နောက် စုစုပေါင်း စတုရန်း၏ ပေါင်းလဒ်ကို တွက်ချက်နိုင်သည်။

ဥပမာ၊ ပထမကျောင်းသားအတွက် စတုရန်းစုစုပေါင်း၏စုစုပေါင်းသည်-

(y _i – y ) ² = (68 – 81) ² = 169 ။

ကျောင်းသားတစ်ဦးစီအတွက် စုစုပေါင်းစတုရန်းများကို ရှာဖွေရန် တူညီသောချဉ်းကပ်နည်းကို အသုံးပြုနိုင်ပါသည်။

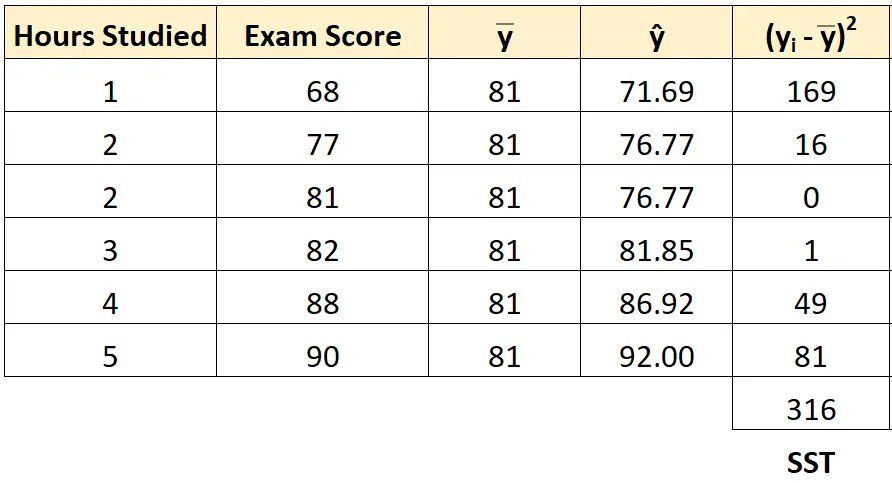
စုစုပေါင်းစတုရန်း၏ပေါင်းလဒ်သည် 316 ဖြစ်သွားသည်။

အဆင့် 4- စတုရန်းဆုတ်ယုတ်မှု၏ပေါင်းလဒ် (SSR) တွက်ချက်ပါ။

ထို့နောက် လေးထောင့်ဆုတ်ယုတ်မှု၏ ပေါင်းလဒ်ကို တွက်ချက်နိုင်သည်။

ဥပမာအားဖြင့်၊ ပထမကျောင်းသားအတွက် နှစ်ထပ်ဆုတ်ယုတ်မှု၏ပေါင်းလဒ်သည်-

( _ŷi – y ) ² = (71.69 – 81) ² = 86.64 ။

ကျောင်းသားတစ်ဦးစီအတွက် နှစ်ထပ်ကိန်းများ၏ ဆုတ်ယုတ်မှုကို ရှာဖွေရန် တူညီသောချဉ်းကပ်နည်းကို အသုံးပြုနိုင်သည်။

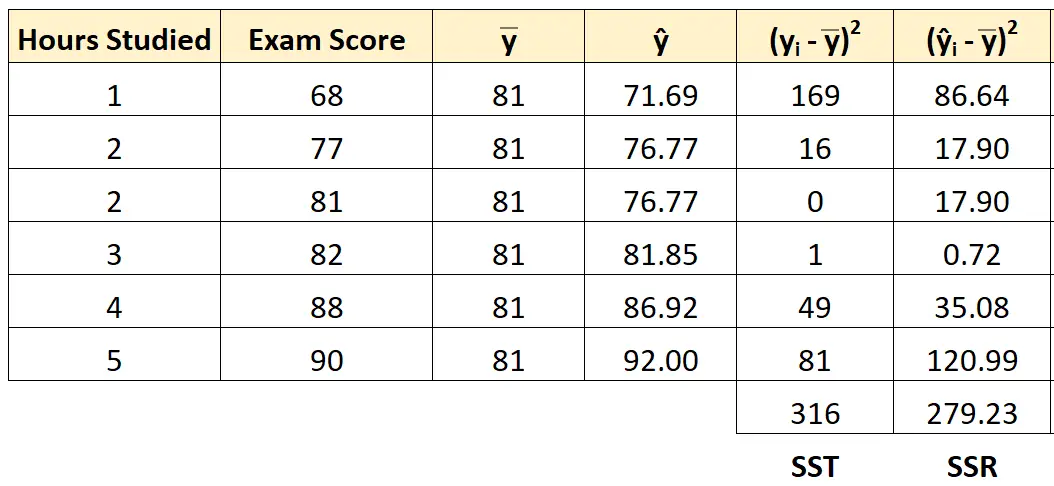
နှစ်ထပ်ဆုတ်ယုတ်မှု၏ပေါင်းလဒ်သည် 279.23 ဖြစ်လာသည်။

အဆင့် 5- စတုရန်းအမှားအမှား (SSE) ၏ပေါင်းလဒ်ကို တွက်ချက်ပါ။

ထို့နောက် လေးထောင့်ပေါင်း၏ အမှားကို တွက်ချက်နိုင်သည်။

ဥပမာ၊ ပထမကျောင်းသားအတွက် စတုရန်းအမှားပေါင်းလဒ်သည်-

(ŷ _i – y _i ) ² = (71.69 – 68) ² = 13.63 ။

ကျောင်းသားတစ်ဦးစီအတွက် စတုရန်းအမှားပေါင်းကို ရှာဖွေရန် တူညီသောချဉ်းကပ်နည်းကို အသုံးပြုနိုင်သည်။

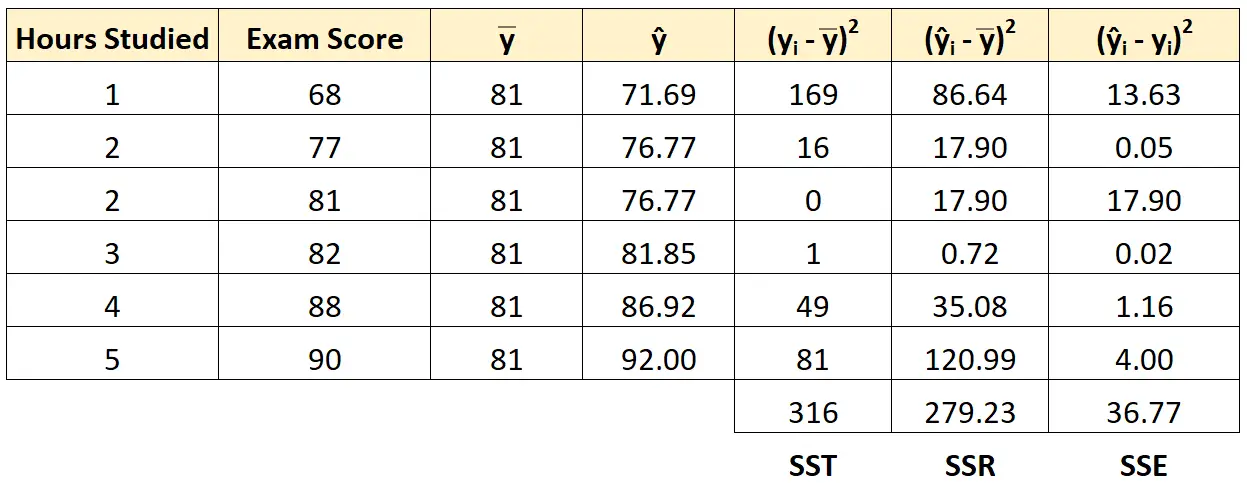
SST = SSR + SSE ကို စစ်ဆေးအတည်ပြုနိုင်ပါသည်။

• SST = SSR + SSE
• 316 = 279.23 + 36.77

အောက်ဖော်ပြပါညီမျှခြင်းကို အသုံးပြု၍ regression model ၏ R နှစ်ထပ်ကိန်းကိုလည်း တွက်ချက်နိုင်သည်။

• R နှစ်ထပ်ကိန်း = SSR/SST
• R နှစ်ထပ် = 279.23/316
• R နှစ်ထပ်ကိန်း = 0.8836

စာမေးပွဲရမှတ်များတွင် ကွဲလွဲမှု 88.36% ကို လေ့လာသည့် နာရီအရေအတွက်ဖြင့် ရှင်းပြနိုင်သည်ဟု ၎င်းကဆိုသည်။

ထပ်လောင်းအရင်းအမြစ်များ

ရိုးရှင်းသော linear regression line အတွက် SST၊ SSR နှင့် SSE ကို အလိုအလျောက်တွက်ချက်ရန် အောက်ပါဂဏန်းတွက်စက်များကို သင်အသုံးပြုနိုင်ပါသည်။

SST ဂဏန်းတွက်စက်
RSS ဂဏန်းတွက်စက်
ESS ဂဏန်းပေါင်းစက်