T-score နှင့် z-score- ၎င်းတို့ကို မည်သည့်အချိန်တွင် အသုံးပြုရမည်နည်း။

စာရင်းအင်းသင်တန်းများတွင် ကျောင်းသားများကို ရှုပ်ထွေးစေသော ဝေါဟာရနှစ်ခုမှာ t-score နှင့် z-scores ဖြစ်သည်။

နှစ်ခုလုံးသည် ယူဆချက်စမ်းသပ်ခြင်း သို့မဟုတ် ယုံကြည်မှုကြားကာလများကို တည်ဆောက်ရာတွင် တွင်ကျယ်စွာအသုံးပြုသော်လည်း ၎င်းတို့သည် အနည်းငယ်ကွဲပြားပါသည်။

ဤသည်မှာ တစ်ခုစီအတွက် ဖော်မြူလာဖြစ်သည်-

ရမှတ် t = ( x – μ) / (s/√ n )

ရွှေ-

• x : နမူနာဆိုလိုသည်။
• μ : လူဦးရေ ပျမ်းမျှ
• s : နမူနာစံသွေဖည်
• n : နမူနာအရွယ်အစား

z-score = ( x – μ) / σ

ရွှေ-

• x : ကုန်ကြမ်းဒေတာတန်ဖိုး
• μ : လူဦးရေ ပျမ်းမျှ
• σ : လူဦးရေစံသွေဖည်

သင့်ဒေတာအပေါ် အခြေခံ၍ တစ်ခုစီကို မည်သည့်အချိန်တွင် အသုံးပြုသင့်သည်ကို ဤအစီအစဥ်ဇယားက ဖော်ပြသည်-

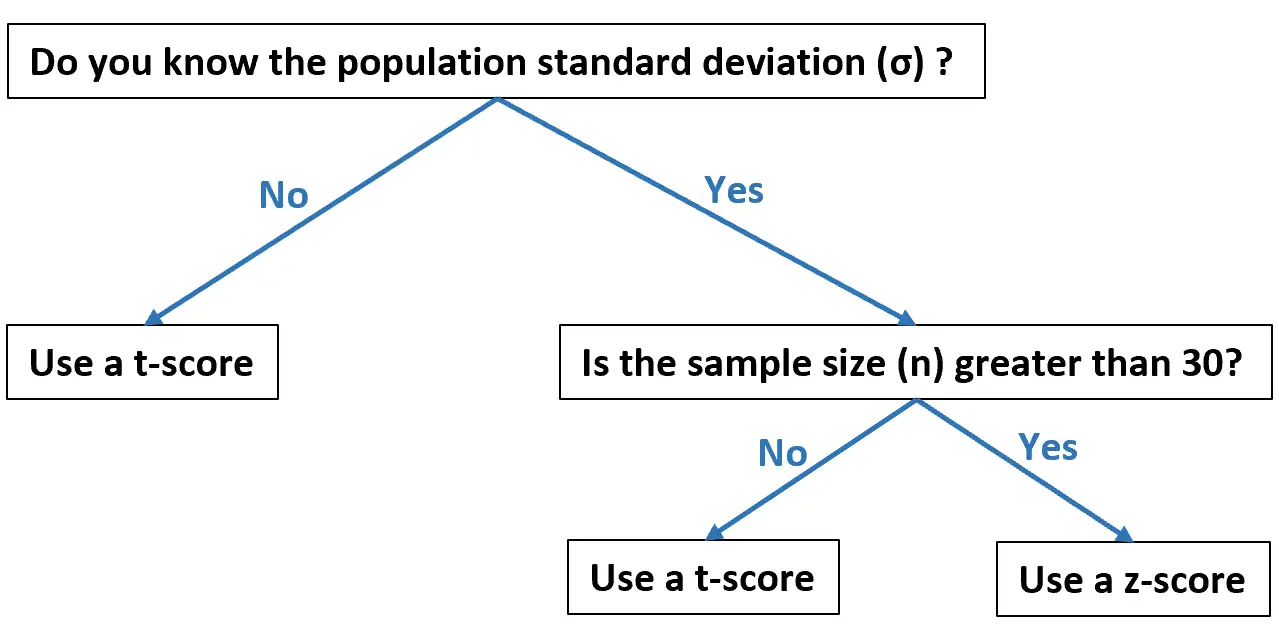
အောက်ဖော်ပြပါ ဥပမာများသည် လက်တွေ့တွင် T-score နှင့် Z-score တွက်ချက်နည်းကို ပြသထားသည်။

ဥပမာ 1- T-Score တွက်ချက်ခြင်း။

စားသောက်ဆိုင်တစ်ဆိုင်သည် ပျမ်းမျှအလေးချိန် μ = 0.25 ပေါင်ရှိသည်ဟုဆိုကာ ဟမ်ဘာဂါပြင်ဆင်သည်ဆိုပါစို့။

ကျွန်ုပ်တို့သည် n = 20 ဟမ်ဘာဂါ၏ ကျပန်းနမူနာကို ယူကာ နမူနာ၏ ပျမ်းမျှအလေးချိန်မှာ x = 0.22 ပေါင်ဖြစ်ပြီး စံသွေဖည်မှု s = 0.05 ပေါင်ဖြစ်သည်ဆိုပါစို့။ ဤစားသောက်ဆိုင်မှ ထုတ်လုပ်သော ဟမ်ဘာဂါအားလုံး၏ အမှန်တကယ် ပျမ်းမျှအလေးချိန်သည် 0.25 ပေါင်နှင့် ညီမျှခြင်းရှိမရှိ ဆုံးဖြတ်ရန် သီအိုရီစစ်ဆေးမှုကို ပြုလုပ်ပါ။

ဤဥပမာအတွက်၊ အောက်ဖော်ပြပါ အခြေအနေနှစ်ခုစလုံးနှင့် မကိုက်ညီသောကြောင့် ယူဆချက်စမ်းသပ်မှုကို လုပ်ဆောင်ရန် T-score ကို အသုံးပြုပါမည်။

• လူဦးရေစံသွေဖည်မှု (σ) ကို သိရှိသည်။ (σ ဤဥပမာတွင် မဖော်ပြထားပါ)
• နမူနာအရွယ်အစားသည် 30 ထက်ကြီးသည်။ (ဤဥပမာတွင် n=20)

ဒီတော့ t-score ကို အောက်ပါအတိုင်း တွက်မယ်။

• ရမှတ် t = ( x – μ) / (s/√ n )
• t-score = (0.22 – 0.25) / (0.05 / √ 20 )
• t-score = -2.68

P-value T-score ဂဏန်းတွက်စက်အရ ၊ ဤ t-score နှင့် ကိုက်ညီသော p-value သည် 0.01481 ဖြစ်သည်။

ဤ p-value သည် 0.05 ထက်နည်းသောကြောင့်၊ ဤစားသောက်ဆိုင်မှထုတ်သော ဟမ်ဘာဂါ၏ပျမ်းမျှအလေးချိန်သည် 0.25 ပေါင်နှင့်ညီမျှသည်မဟုတ်ကြောင်းပြောရန် လုံလောက်သောအထောက်အထားရှိသည်။

ဥပမာ 2- Z ရမှတ်ကို တွက်ချက်ခြင်း။

ကုမ္ပဏီတစ်ခုသည် μ = 20 နာရီ ပျမ်းမျှ နှင့် σ = 5 နာရီ ၏ စံသွေဖည်မှုဖြင့် ပုံမှန် ဖြန့်ဖြူးမှုကို လိုက်နာရန် သက်တမ်းကို သိရှိထားသော ဘက်ထရီများ ထုတ်လုပ်သည်ဟု ယူဆပါ။

ကျွန်ုပ်တို့သည် n=50 ဘက်ထရီကို ကျပန်းနမူနာယူ၍ နမူနာဆိုလိုသည်မှာ x = 21 နာရီဖြစ်သည်ဆိုပါစို့။ ဤကုမ္ပဏီမှထုတ်လုပ်သော ဘက်ထရီအားလုံး၏ ပျမ်းမျှသက်တမ်းသည် နာရီ 20 နှင့် ညီမျှခြင်းရှိ၊ မရှိ ဆုံးဖြတ်ရန် သီအိုရီစမ်းသပ်မှုကို ပြုလုပ်ပါ။

ဤဥပမာအတွက်၊ အောက်ပါအခြေအနေနှစ်ခုစလုံးနှင့်ကိုက်ညီသောကြောင့် သီအိုရီစစ်ဆေးမှုကိုလုပ်ဆောင်ရန် z-score ကို အသုံးပြုပါမည်။

• လူဦးရေစံသွေဖည်မှု (σ) ကို သိရှိသည်။ (σ သည် ဤဥပမာတွင် 5 နှင့် ညီမျှသည်)
• နမူနာအရွယ်အစားသည် 30 ထက်ကြီးသည်။ (ဤဥပမာတွင် n=50)

ထို့ကြောင့် z-score ကို အောက်ပါအတိုင်း တွက်ချက်ပါမည်။

• z-score = ( x – μ) / σ
• z-score = (21 – 20) / 5
• z-ရမှတ် = 0.2

P-value Z-score ဂဏန်းတွက်စက်အရ၊ ဤ z-score နှင့် ကိုက်ညီသော p-value သည် 0.84184 ဖြစ်သည်။

ဤ p-value သည် 0.05 ထက်မနည်းသောကြောင့်၊ ဤကုမ္ပဏီမှထုတ်လုပ်သော ဘက်ထရီအားလုံး၏ပျမ်းမျှသက်တမ်းသည် နာရီ 20 နှင့်ကွာခြားသည်ဟုဆိုရန်လုံလောက်သောအထောက်အထားမရှိပါ။

ထပ်လောင်းအရင်းအမြစ်များ

အောက်ပါသင်ခန်းစာများသည် T ရမှတ်များနှင့် Z ရမှတ်များအကြောင်း နောက်ထပ်အချက်အလက်များကို ပေးဆောင်သည်-

ပုံမှန်ဖြန့်ဖြူးမှုနှင့် t ဖြန့်ဖြူးမှု- ကွာခြားချက်ကား အဘယ်နည်း။
ဖြန့်ချီရေးဇယား t ကိုဖတ်နည်း
Z ဇယားဖတ်နည်း