Excel တွင် နမူနာ t-test နှစ်ခုကို မည်သို့လုပ်ဆောင်ရမည်နည်း။
နမူနာနှစ်ခု t-test ကို လူဦးရေ နှစ်ခု၏ အဓိပ္ပါယ်သည် ညီမျှခြင်း ရှိ၊ မရှိ စမ်းသပ်ရန် အသုံးပြုပါသည်။
ဤသင်ခန်းစာသည် Excel တွင် နမူနာနှစ်ခု t-test ကို မည်သို့လုပ်ဆောင်ရမည်ကို ရှင်းပြထားသည်။
Excel တွင် နမူနာ t-test နှစ်ခုကို မည်သို့လုပ်ဆောင်ရမည်နည်း။
နိုင်ငံတစ်ခုတွင် မတူညီသောအပင်မျိုးစိတ်နှစ်ခုသည် ပျမ်းမျှအမြင့်တူညီမှုရှိမရှိကို သုတေသီများ သိလိုသည်ဆိုပါစို့။ အပင်တစ်ပင်ချင်းစီကို တိုင်းတာရန် အချိန်ကြာလွန်းသောကြောင့် မျိုးစိတ်တစ်ခုစီ၏ အပင် 20 ကို နမူနာယူရန် ဆုံးဖြတ်ခဲ့သည်။
အောက်ဖော်ပြပါပုံသည် နမူနာတစ်ခုစီရှိ အပင်တစ်ခုစီ၏ အမြင့် (လက်မဖြင့်) ကို ပြသသည်-
ဤအဆင့်များကို လိုက်နာခြင်းဖြင့် မျိုးစိတ်နှစ်ခု၏ ပျမ်းမျှအမြင့်ရှိမရှိ ဆုံးဖြတ်ရန် နမူနာနှစ်ခု t-test ကို လုပ်ဆောင်နိုင်သည်-
အဆင့် 1- လူဦးရေကွဲလွဲမှု တူညီခြင်းရှိမရှိ ဆုံးဖြတ်ပါ ။
နမူနာနှစ်ခု t-test ကို ပြုလုပ်သောအခါ လူဦးရေ နှစ်ခုသည် တူညီသည် သို့မဟုတ် မညီမျှသော ကွဲလွဲမှုများ ရှိမရှိကို ဦးစွာ ဆုံးဖြတ်ရပါမည်။ ယေဘူယျအားဖြင့်၊ အများဆုံးနမူနာကွဲလွဲမှု၏ အသေးဆုံးနမူနာကွဲလွဲချက်နှင့် အသေးဆုံးနမူနာကွဲလွဲမှုအချိုးသည် 4:1 ထက်နည်းပါက လူဦးရေများတွင် တူညီသောကွဲလွဲမှုများရှိသည်ဟု ကျွန်ုပ်တို့ယူဆနိုင်ပါသည်။
အောက်ပါပုံတွင်ပြထားသည့်အတိုင်း Excel လုပ်ဆောင်ချက် =VAR.S(ဆဲလ်အကွာအဝေး) ကို အသုံးပြု၍ နမူနာတစ်ခုစီအတွက် ကွဲလွဲမှုကို ကျွန်ုပ်တို့ ရှာဖွေနိုင်သည်-
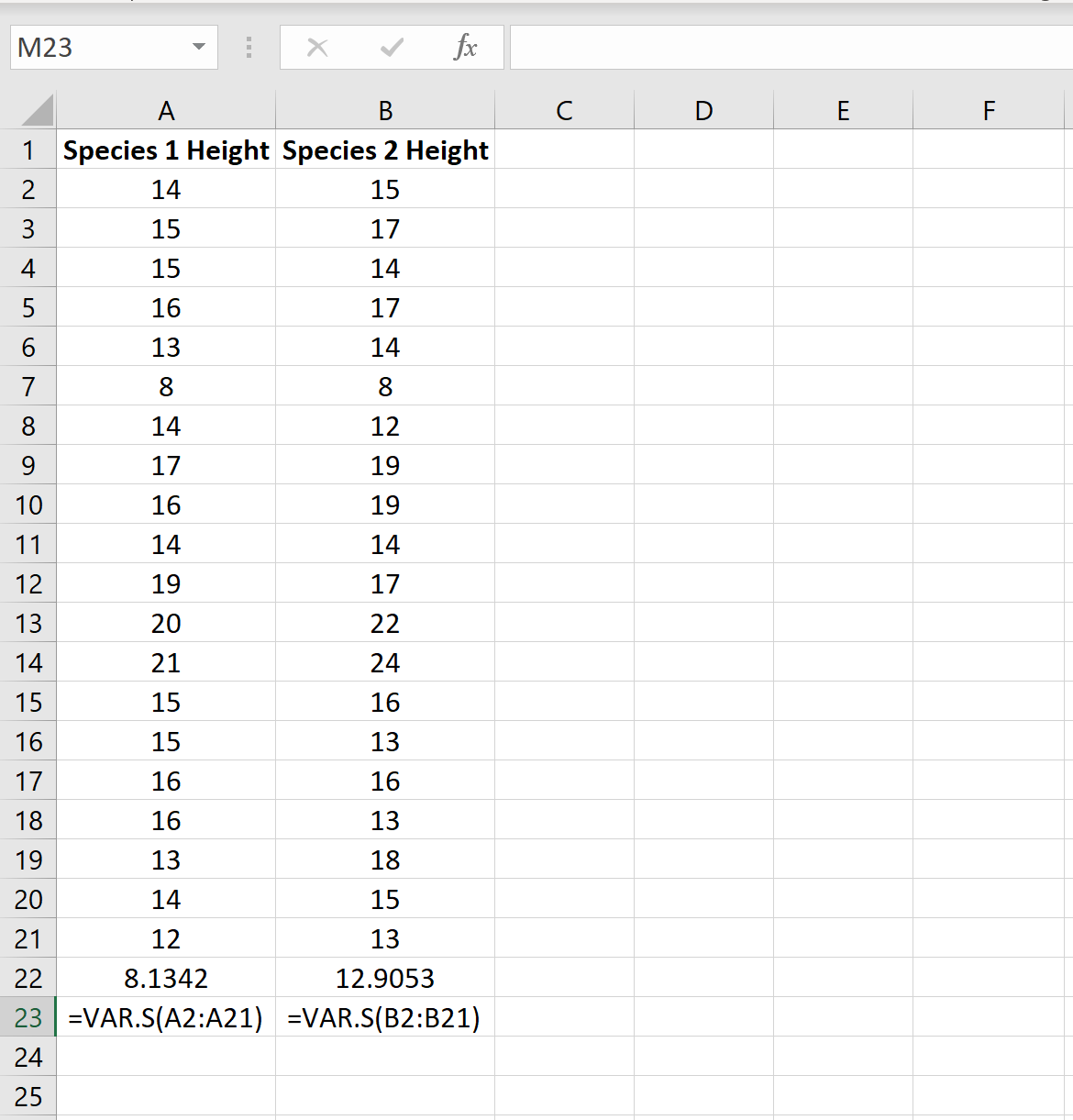
အငယ်ဆုံးနမူနာကွဲလွဲချက်နှင့် အကြီးဆုံးနမူနာကွဲလွဲမှု၏အချိုးသည် 12.9053/8.1342 = 1.586 ဖြစ်ပြီး 4 ထက်နည်းသည်။ ဆိုလိုသည်မှာ လူဦးရေကွဲလွဲမှု တူညီသည်ဟု ကျွန်ုပ်တို့ ယူဆနိုင်သည်။
အဆင့် 2- Analysis ToolPak ကိုဖွင့်ပါ ။
ထိပ်ဖဲကြိုး၏ ဒေတာတက်ဘ်တွင် “ဒေတာခွဲခြမ်းစိတ်ဖြာခြင်း” ကိုနှိပ်ပါ။
နှိပ်ရန် ဤရွေးချယ်မှုကို မတွေ့ပါက၊ လုံးဝအခမဲ့ဖြစ်သည့် Analysis ToolPak ကို ဒေါင်းလုဒ်လုပ်ရန် လိုအပ်ပါသည်။
အဆင့် 3- အသုံးပြုရန် သင့်လျော်သော စမ်းသပ်မှုကို ရွေးချယ်ပါ။
t-test ဟုပြောသော ရွေးစရာကို ရွေးပါ- တူညီသောကွဲလွဲမှုများဟု ယူဆသော နမူနာနှစ်ခုကို ရွေးပါ ၊ ထို့နောက် OK ကိုနှိပ်ပါ။
အဆင့် 4: လိုအပ်သောအချက်အလက်များကိုထည့်ပါ ။
variable 1 (ကျွန်ုပ်တို့၏ပထမနမူနာ)၊ variable 2 (ကျွန်ုပ်တို့၏ဒုတိယနမူနာ)၊ hypothetical mean ခြားနားချက် (ဤအခြေအနေတွင်၊ ကျွန်ုပ်တို့သည် “ 0” ကို ထည့်ထားသောကြောင့် လူဦးရေအစစ်အမှန်၏ ဆိုလိုရင်းကွာခြားချက်မှာ 0 ဖြစ်မဖြစ် သိလိုသောကြောင့်၊ နှင့် t-test ရလဒ်များကို ပြသလိုသည့် အထွက်အကွာအဝေး။ ထို့နောက် OK ကိုနှိပ်ပါ။
အဆင့် 5- ရလဒ်များကို ဘာသာပြန်ပါ ။
ယခင်အဆင့်တွင် OK ကိုနှိပ်လိုက်သည်နှင့် t-test ရလဒ်များကို ပြသမည်ဖြစ်သည်။
ဤသည်မှာ ရလဒ်များကို မည်သို့အဓိပ္ပာယ်ဖွင့်ဆိုနိုင်သည်-
ပျမ်းမျှ- ဤသည်မှာ နမူနာတစ်ခုစီ၏ ပျမ်းမျှဖြစ်သည်။ နမူနာ 1 တွင် ပျမ်းမျှ အမြင့် 15.15 ရှိပြီး နမူနာ 2 သည် ပျမ်းမျှ အမြင့် 15.8 ရှိသည်။
ကွဲပြားမှု- ဤသည်မှာ နမူနာတစ်ခုစီအတွက် ကွဲလွဲမှုဖြစ်သည်။ နမူနာ 1 တွင် ကွဲလွဲမှု 8.13 ရှိပြီး နမူနာ 2 တွင် ကွဲလွဲမှု 12.90 ရှိသည်။
လေ့လာတွေ့ရှိချက်များ- ဤသည်မှာ နမူနာတစ်ခုစီရှိ လေ့လာတွေ့ရှိချက်အရေအတွက်ဖြစ်သည်။ နမူနာနှစ်ခုလုံးတွင် လေ့လာတွေ့ရှိချက် 20 ပါရှိသည် (ဥပမာ နမူနာတစ်ခုစီတွင် အပင် 20 စီ)။
ပေါင်းစပ်ကွဲလွဲမှု- ဖော်မြူလာ s 2 p = [ (n 1 -1)s 2 1 + (n 2 -1)s 2 2 2 2 ] / (n 1 +n 2 – 2) 10.51974 ဖြစ်လာသည်။ ထို့နောက် t -test statistic ကို တွက်ချက်ရာတွင် ဤနံပါတ်ကို အသုံးပြုပါသည်။
Hypothetical Mean Difference- ကျွန်ုပ်တို့ “ ယူဆချက်” နှင့် ပတ်သက်သော အရေအတွက်သည် လူဦးရေနှစ်ခု၏ အဓိပ္ပါယ်များကြား ကွာခြားချက်ဖြစ်သည်။ ဤအခြေအနေတွင်၊ လူဦးရေနှစ်ခု၏ ကွာခြားချက်သည် 0 နှင့် ညီမျှသည်ရှိမရှိ စမ်းသပ်လိုသောကြောင့် 0 ကို ရွေးချယ်ခဲ့ခြင်းဖြစ်သည်၊ ဥပမာအားဖြင့် ကွာခြားမှုမရှိပါက၊
df- t-test အတွက် လွတ်လပ်မှုဒီဂရီ၊ n 1 + n 2 -2 = 20 + 20 – 2 = 38 ။
t Stat- စမ်းသပ်စာရင်းအင်း t ၊ t = [ x 1 – x 2 ] / √ [s 2 p (1/n 1 + 1/n 2 )]
ဤကိစ္စတွင်၊ t = [15.15-15.8] / √ [10.51974(1/20+1/20)] = -0.63374 ။
Two-tailed P(T<=t) : two-tailed t test အတွက် p-တန်ဖိုး။ ဤကိစ္စတွင်၊ p = 0.530047 ။ ၎င်းသည် alpha = 0.05 ထက် များစွာကြီးမားသောကြောင့် null hypothesis ကို ငြင်းပယ်ရန် ပျက်ကွက်ပါသည်။ လူဦးရေ နှစ်ခု၏ အဓိပ္ပါယ်မှာ ကွဲပြားသည်ဟု ဆိုရန် လုံလောက်သော အထောက်အထား မရှိပါ။
t Two-tailed Critical- ဤသည်မှာ alpha = 0.05 နှင့် df = 38 ပါသော t-distribution table မှ တန်ဖိုးကို ခွဲခြားသတ်မှတ်ခြင်းဖြင့် တွေ့ရှိသော စစ်ဆေးမှု၏ အရေးပါသောတန်ဖိုးဖြစ်ပါသည်။ ၎င်းသည် 2 ဖြစ်သည်၊ ၀၂၄၃၉၄ ။ ကျွန်ုပ်တို့၏ t- စမ်းသပ်မှုကိန်းဂဏန်းသည် ဤတန်ဖိုးထက်နည်းသောကြောင့်၊ ကျွန်ုပ်တို့သည် null hypothesis ကို ငြင်းပယ်ရန်ပျက်ကွက်ပါသည်။ လူဦးရေ နှစ်ခု၏ အဓိပ္ပါယ်မှာ ကွဲပြားသည်ဟု ဆိုရန် လုံလောက်သော အထောက်အထား မရှိပါ။
p-value နှင့် critical value ချဉ်းကပ်မှု နှစ်ခုလုံးသည် တူညီသော နိဂုံးသို့ ဦးတည်သွားမည်ကို သတိပြုပါ။
ထပ်လောင်းအရင်းအမြစ်များ
အောက်ဖော်ပြပါ သင်ခန်းစာများသည် Excel တွင် အခြားသော t-test အမျိုးအစားများကို မည်သို့လုပ်ဆောင်ရမည်ကို ရှင်းပြထားပါသည်။
Excel တွင် နမူနာ t-test ကို မည်သို့လုပ်ဆောင်ရမည်နည်း။
Excel တွင်တွဲထားသောနမူနာများကို t-test လုပ်နည်း
စာရေးသူအကြောင်း
Benjamin Anderson
မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။