Excel တွင် triangular distribution ကိုအသုံးပြုနည်း (ဥပမာများဖြင့်)
တြိဂံပုံသဏ္ဍာန်ဖြန့်ဝေမှုသည် တြိဂံပုံသဏ္ဍာန်ဖြစ်နိုင်ခြေသိပ်သည်းဆလုပ်ဆောင်မှုဖြင့် စဉ်ဆက်မပြတ်ဖြစ်နိုင်ခြေဖြန့်ဝေမှုတစ်ခုဖြစ်သည်။
၎င်းကို တန်ဖိုးသုံးခုဖြင့် သတ်မှတ်သည်။
- အနိမ့်ဆုံး တန်ဖိုးရှိတယ်။
- အမြင့်ဆုံးတန်ဖိုး b
- အမြင့်ဆုံးတန်ဖိုး c
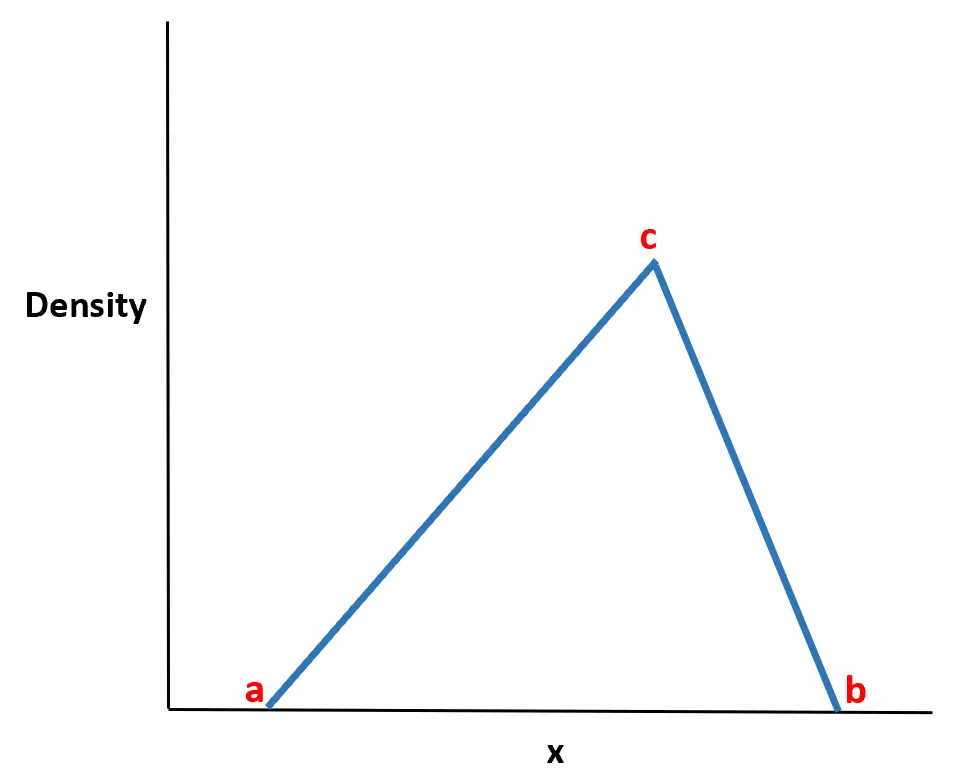
ဖြန့်ဖြူးမှု၏အမည်သည် ဖြစ်နိုင်ခြေသိပ်သည်းဆလုပ်ဆောင်မှုတွင် တြိဂံပုံသဏ္ဍာန်ရှိသည်ဟူသောအချက်မှ ဆင်းသက်လာခြင်းဖြစ်သည်။
တြိဂံပုံဖြန့်ဝေမှုတွင် အောက်ပါ PDF နှင့် CDF ပါရှိသည်။
PDF-
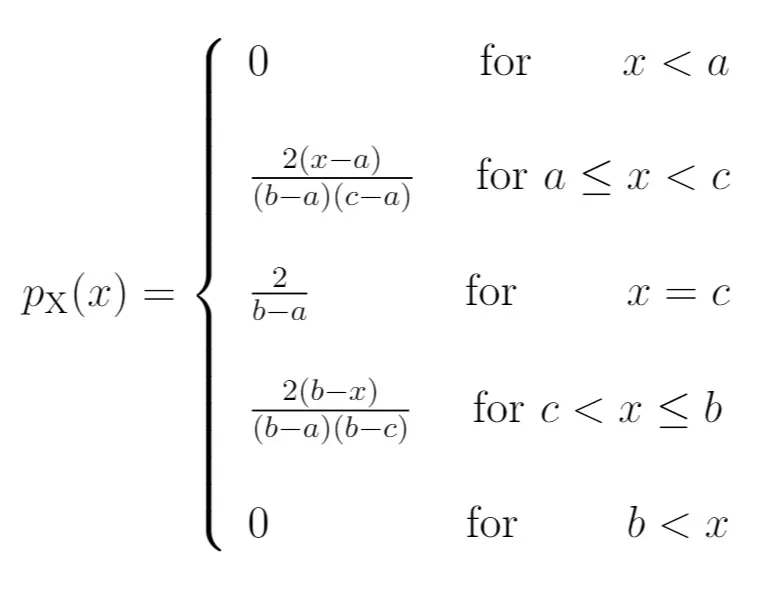
CDF-
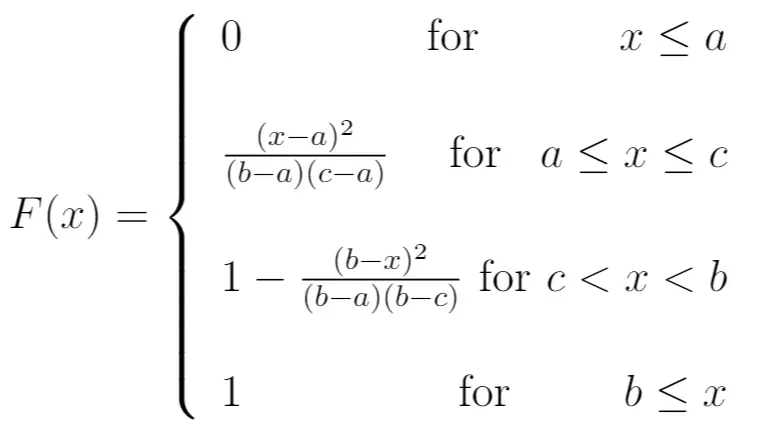
အောက်ဖော်ပြပါနမူနာများသည် Excel တွင်ဖြစ်နိုင်ခြေများကိုတွက်ချက်ရန် triangular distribution ကိုအသုံးပြုပုံကိုပြသထားသည်။
ဥပမာ 1- စားသောက်ဆိုင် အရောင်း
စားသောက်ဆိုင်တစ်ဆိုင်သည် လာမည့်အပတ်အတွက် စုစုပေါင်းရောင်းချရမှုမှာ အနည်းဆုံး $10,000၊ အများဆုံး $30,000 နှင့် အများဆုံး $25,000 ဖြစ်လိမ့်မည်ဟု ခန့်မှန်းဆိုကြပါစို့။

စားသောက်ဆိုင်တွင် စုစုပေါင်းရောင်းအား $20,000 အောက် ဖြစ်နိုင်ခြေအဘယ်နည်း။
CDF အရ၊ စုစုပေါင်းရောင်းအား $20,000 အောက်ဖြစ်နိုင်ခြေကို ရှာဖွေရန် အောက်ပါဖော်မြူလာကို အသုံးပြုနိုင်ပါသည်။
- P(X < x) = (xa) 2 / (ba)(ca))
ဤတွင် Excel တွင် ဤဖြစ်နိုင်ခြေကို တွက်ချက်နည်း။
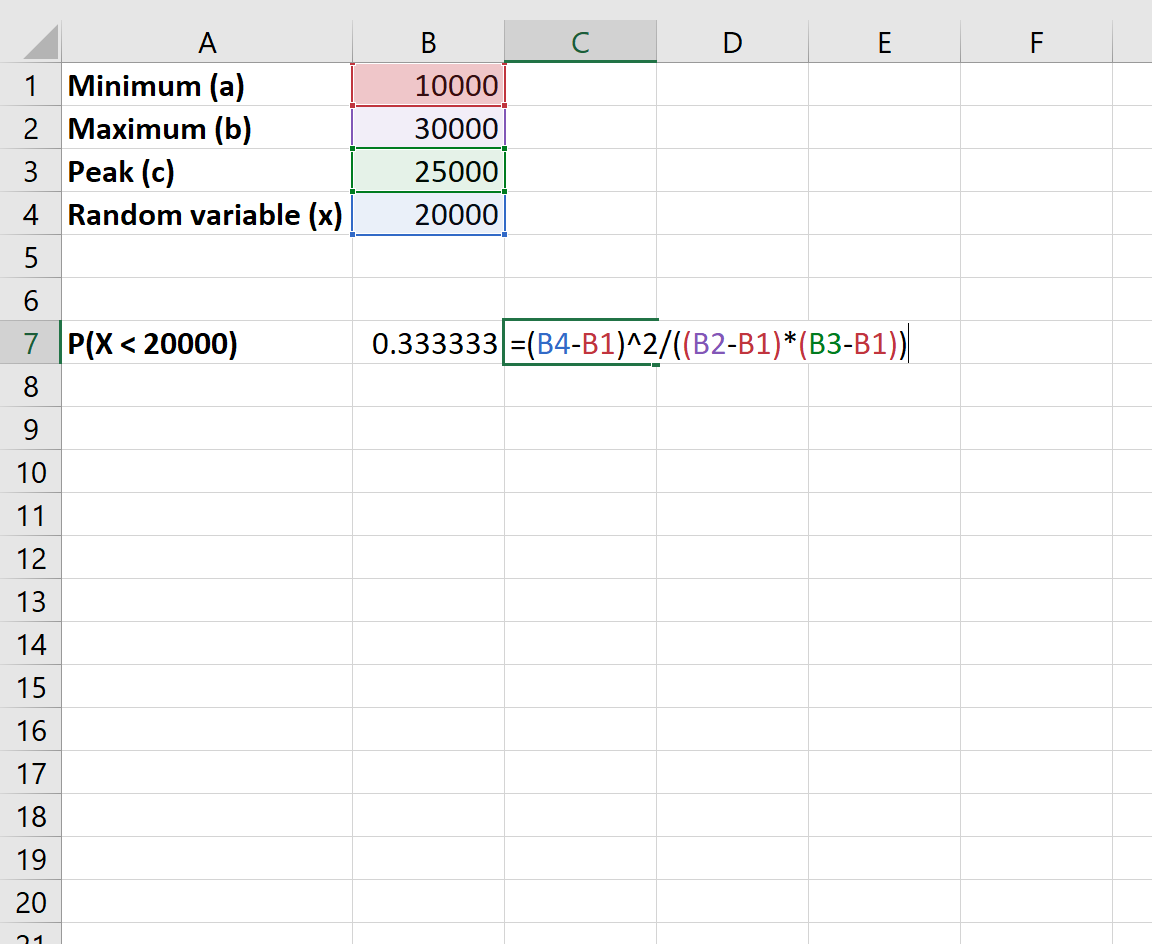
စားသောက်ဆိုင်တွင် စုစုပေါင်းရောင်းအား $20,000 အောက်ရှိနိုင်ခြေမှာ 0.333 ဖြစ်သည်။
ဥပမာ 2- ဖောက်သည်အရေအတွက်
သတ်မှတ်ရက်သတ္တပတ်အတွင်း လာမည့်ဖောက်သည်အရေအတွက်သည် အနည်းဆုံး 500၊ အများဆုံး 2,000 နှင့် အများဆုံး 1,200 ဖြစ်နိုင်သည်ဟု စတိုးဆိုင်တစ်ခုမှ ခန့်မှန်းသည်ဆိုကြပါစို့။
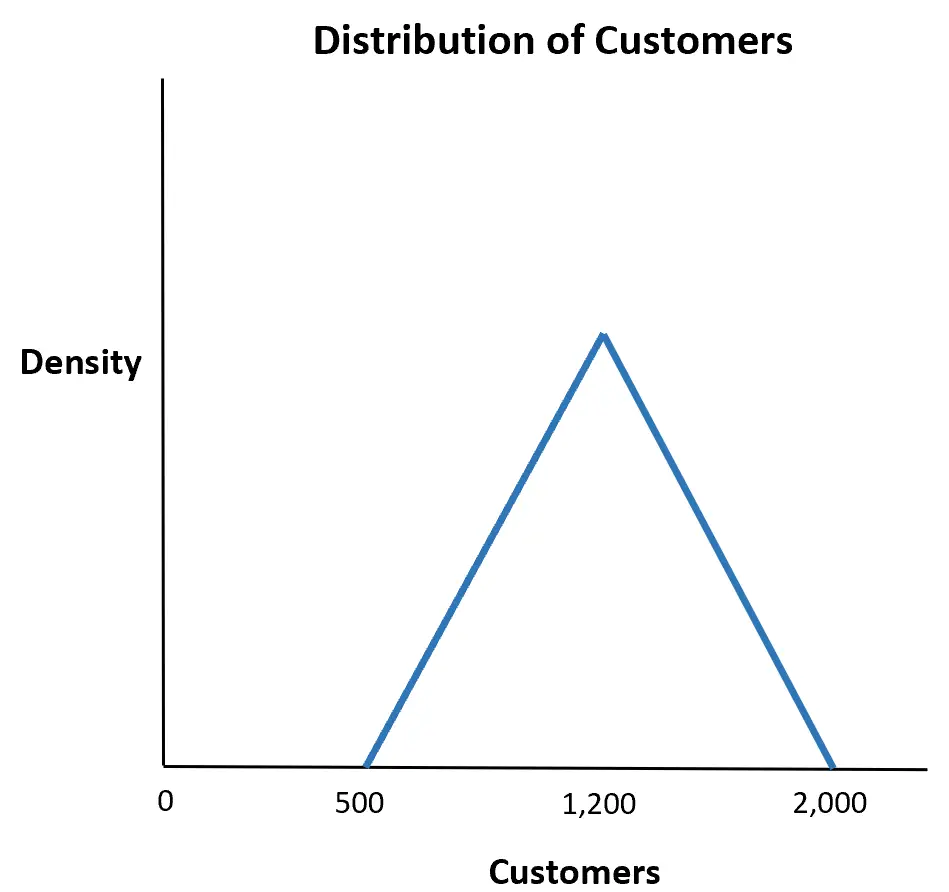
သတ်မှတ်ရက်သတ္တပတ်အတွင်း စတိုးဆိုင်သို့ဖောက်သည် 1,500 ကျော်ဝင်ရောက်နိုင်ခြေအဘယ်နည်း။
CDF အရ၊ ကျွန်ုပ်တို့သည် သုံးစွဲသူစုစုပေါင်း 1,500 ထက်များသော ဖြစ်နိုင်ခြေကို ရှာဖွေရန် အောက်ပါဖော်မြူလာကို အသုံးပြုနိုင်ပါသည်။
- P(X > x) = 1 – [1 – (bx) 2 / ((ba)(bc))]
ဤတွင် Excel တွင် ဤဖြစ်နိုင်ခြေကို တွက်ချက်နည်း။
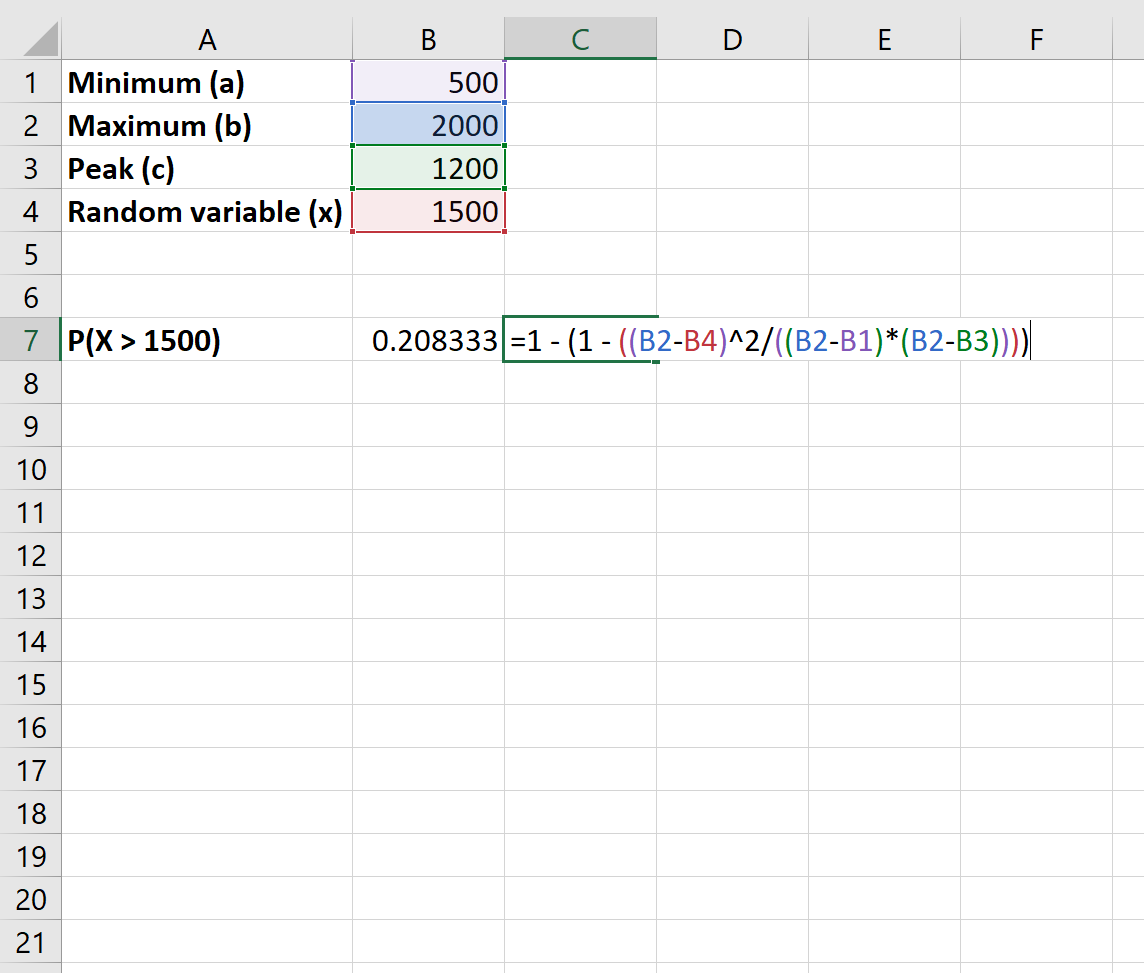
စတိုးဆိုင်သို့ဖောက်သည် 1,500 ကျော်ဝင်ရောက်နိုင်ခြေသည် 0.208 ဖြစ်သည်။
ထပ်လောင်းအရင်းအမြစ်များ
အောက်ဖော်ပြပါ သင်ခန်းစာများသည် Excel တွင် အခြားဖြစ်နိုင်ခြေဖြန့်ဝေမှုများကို မည်သို့အသုံးပြုရကြောင်း ရှင်းပြသည်-
Excel တွင် binomial distribution ကိုအသုံးပြုနည်း
Excel တွင် Poisson distribution ကိုအသုံးပြုနည်း
Excel တွင် ယူနီဖောင်းဖြန့်ချီနည်းကို အသုံးပြုနည်း