Excel တွင် tukey-kramer post hoc test ကို မည်သို့လုပ်ဆောင်ရမည်နည်း။

တစ်လမ်းသွား ANOVA ကို သုံးသော သို့မဟုတ် ထို့ထက်ပိုသော လွတ်လပ်သော အုပ်စုများကြားတွင် စာရင်းအင်းဆိုင်ရာ သိသာထင်ရှားသော ခြားနားမှု ရှိ၊ မရှိ ဆုံးဖြတ်ရန် အသုံးပြုသည်။

ANOVA တွင်အသုံးပြုသော ယူဆချက်များမှာ အောက်ပါအတိုင်းဖြစ်သည်။

null hypothesis (H ₀ ) : µ ₁ = µ ₂ = µ ₃ = … = µ _k (အုပ်စုတစ်ခုစီအတွက် တူညီသည်)

အခြားယူဆချက်- (ဟာ)- အနည်းဆုံး အဓိပ္ပါယ်မှာ အခြားနည်းလမ်းများနှင့် ကွဲပြားသည်။

ANOVA ၏ p-value သည် အရေးပါသည့်အဆင့်အောက်တွင် ရှိနေပါက၊ ကျွန်ုပ်တို့သည် null hypothesis ကို ငြင်းပယ်နိုင်ပြီး အနည်းဆုံး အုပ်စု၏ နည်းလမ်းတစ်ခုသည် အခြားနည်းလမ်းများနှင့် ကွဲပြားသည်ဟု ဆိုရန် လုံလောက်သော အထောက်အထားရှိသည်ဟု ကျွန်ုပ်တို့တွင် ကောက်ချက်ချနိုင်ပါသည်။

သို့သော် မည်သည့် အဖွဲ့များ အချင်းချင်း ကွဲပြားသည်ကို ဤအရာက ကျွန်ုပ်တို့အား မပြောပါ။ ၎င်းသည် ကျွန်ုပ်တို့အား အုပ်စု ပျမ်းမျှ ပျမ်းမျှအားလုံး မညီမျှကြောင်း ရိုးရှင်းစွာ ပြောပြသည်။ ဘယ်အဖွဲ့တွေက တစ်ခုနဲ့တစ်ခု မတူဘူးဆိုတာ အတိအကျသိဖို့အတွက် post hoc test လုပ်ဖို့လိုပါတယ်။

အများဆုံးအသုံးအများဆုံး post hoc စမ်းသပ်မှုသည် Tukey-Kramer စမ်းသပ်မှု ဖြစ်ပြီး၊ အုပ်စုတစ်ခုစီ၏ pairwise ပေါင်းစပ်မှုအကြားပျမ်းမျှအား နှိုင်းယှဉ်ပေးသည်။

အောက်ပါဥပမာသည် Excel တွင် Tukey-Kramer စမ်းသပ်မှုကို မည်သို့လုပ်ဆောင်ရမည်ကို ပြသထားသည်။

ဥပမာ- Excel တွင် Tukey-Kramer စမ်းသပ်မှု

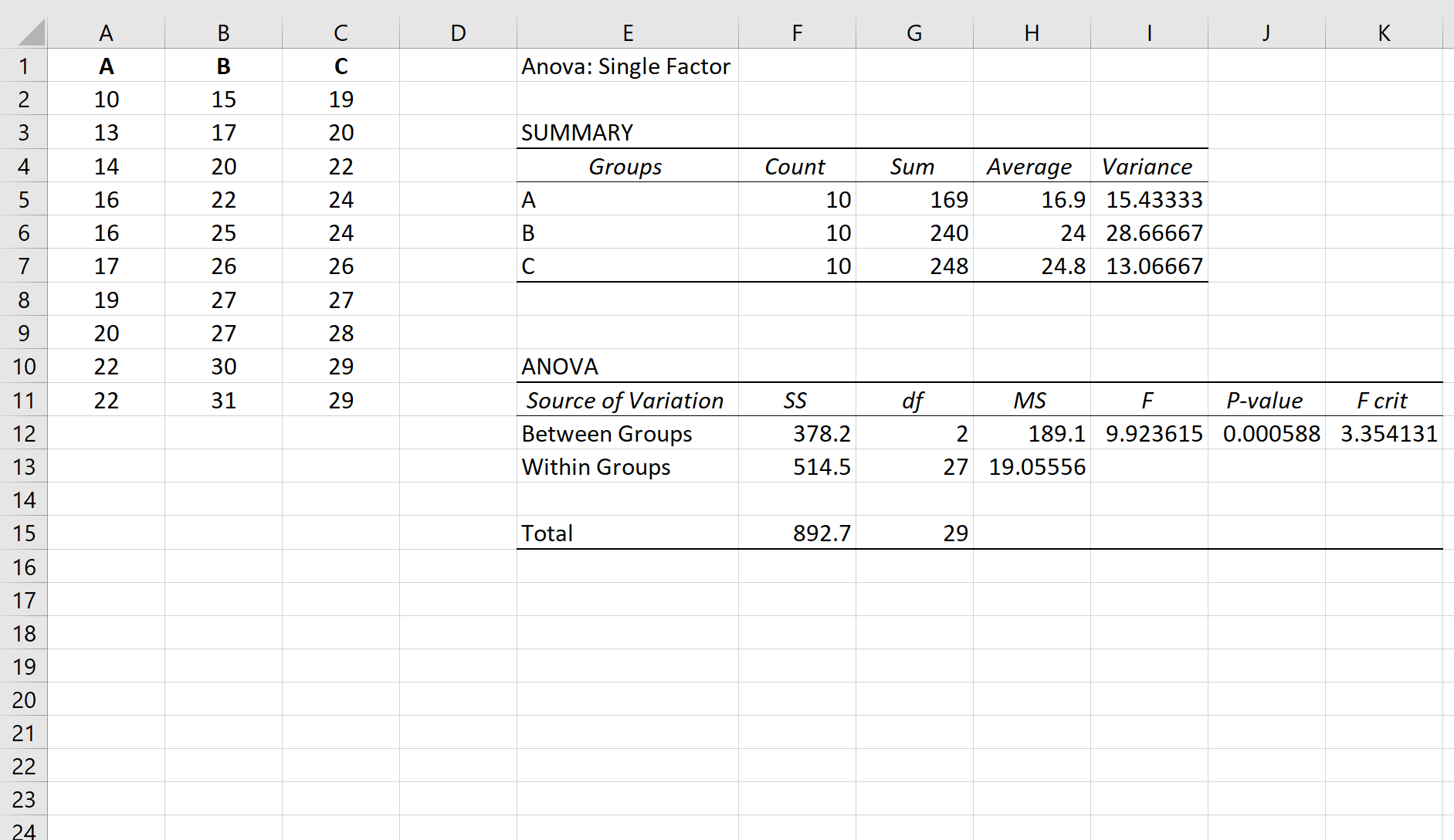
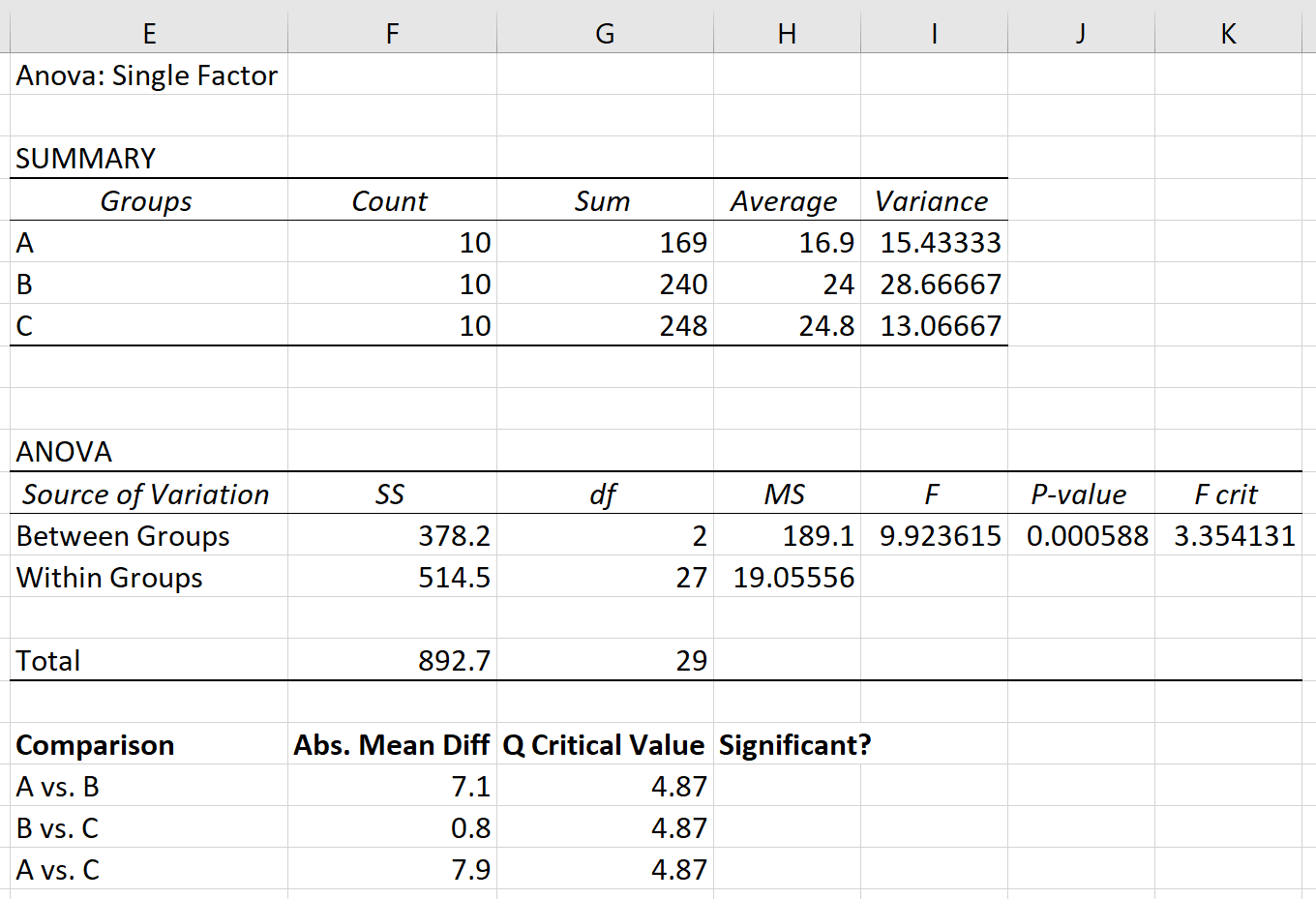
A, B, နှင့် C အုပ်စုသုံးစုတွင် တစ်လမ်းမောင်း ANOVA ကို လုပ်ဆောင်သည်ဆိုပါစို့။ တစ်လမ်းမောင်း ANOVA ၏ရလဒ်များကို အောက်တွင်ဖော်ပြထားသည်-

ဆက်စပ်- Excel တွင် One-Way ANOVA လုပ်ဆောင်နည်း

ANOVA ဇယား၏ p-တန်ဖိုးသည် 0.000588 ဖြစ်သည်။ ဤ p-value သည် 0.05 ထက်နည်းသောကြောင့်၊ ကျွန်ုပ်တို့သည် null hypothesis ကို ငြင်းပယ်နိုင်ပြီး အုပ်စုသုံးစုကြားရှိ ဆိုလိုရင်းမှာ မညီဟု ကောက်ချက်ချနိုင်သည်။

မည်သည့် အဖွဲ့၏ အဓိပ္ပါယ်သည် ကွဲပြားသည်ကို အတိအကျ ဆုံးဖြတ်ရန်၊ ကျွန်ုပ်တို့သည် အောက်ပါအဆင့်များကို အသုံးပြု၍ Tukey-Kramer post hoc စမ်းသပ်မှုကို လုပ်ဆောင်နိုင်သည်-

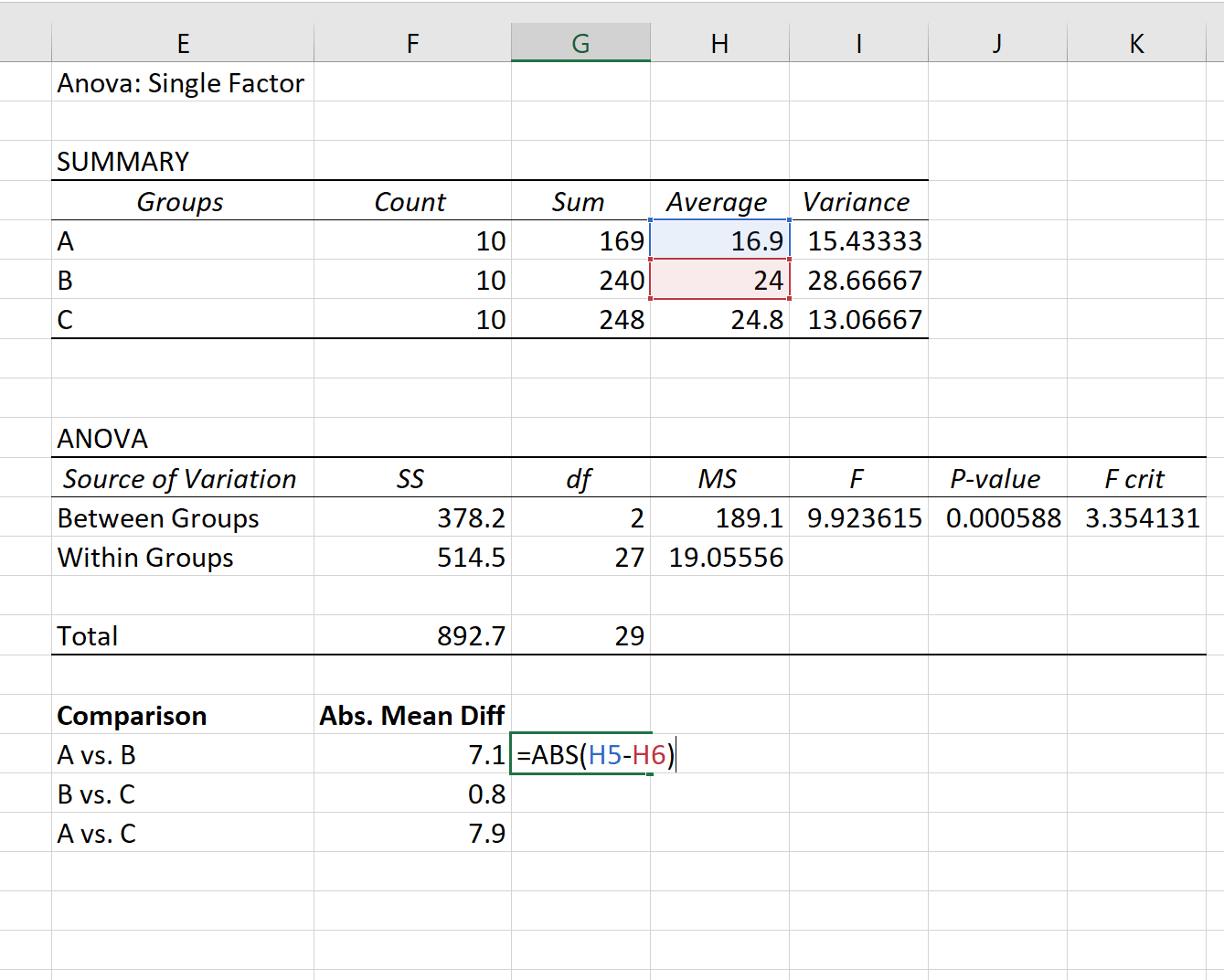
အဆင့် 1- အုပ်စုတစ်ခုစီကြားရှိ ပကတိပျမ်းမျှ ခြားနားချက်ကို ရှာပါ။

ဦးစွာ၊ ANOVA ရလဒ်၏ပထမဇယားတွင်ဖော်ပြထားသောနည်းလမ်းများကိုအသုံးပြုပြီးအုပ်စုတစ်ခုစီအကြားအကြွင်းမဲ့ပျမ်းမျှကွာခြားချက်ကိုကျွန်ုပ်တို့တွေ့ရှိပါမည်-

အဆင့် 2- Q ၏ အရေးပါသောတန်ဖိုးကို ရှာပါ။

ထို့နောက်၊ အောက်ပါဖော်မြူလာကို အသုံးပြု၍ Q ၏ အရေးပါသောတန်ဖိုးကို ရှာဖွေရန် လိုအပ်ပါသည်။

အရေးပါသောတန်ဖိုး Q = Q*√(s ² _{အုပ်စုဖွဲ့ထားသည်} / n.)

ရွှေ-

• Q = Student Table Q ၏ အကွာအဝေးတန်ဖိုး
• s ² _pooled = အုပ်စုအားလုံးတွင် ကွဲလွဲမှု ပေါင်းစပ်ထားသည်။
• မဟုတ်ဘူး = ပေးထားသောအဖွဲ့အတွက် နမူနာအရွယ်အစား

Q တန်ဖိုးကိုရှာရန်၊ သင်သည် ဤကဲ့သို့ပုံပါသော Studentized range Q ဇယားကို ကိုးကားနိုင်သည်-

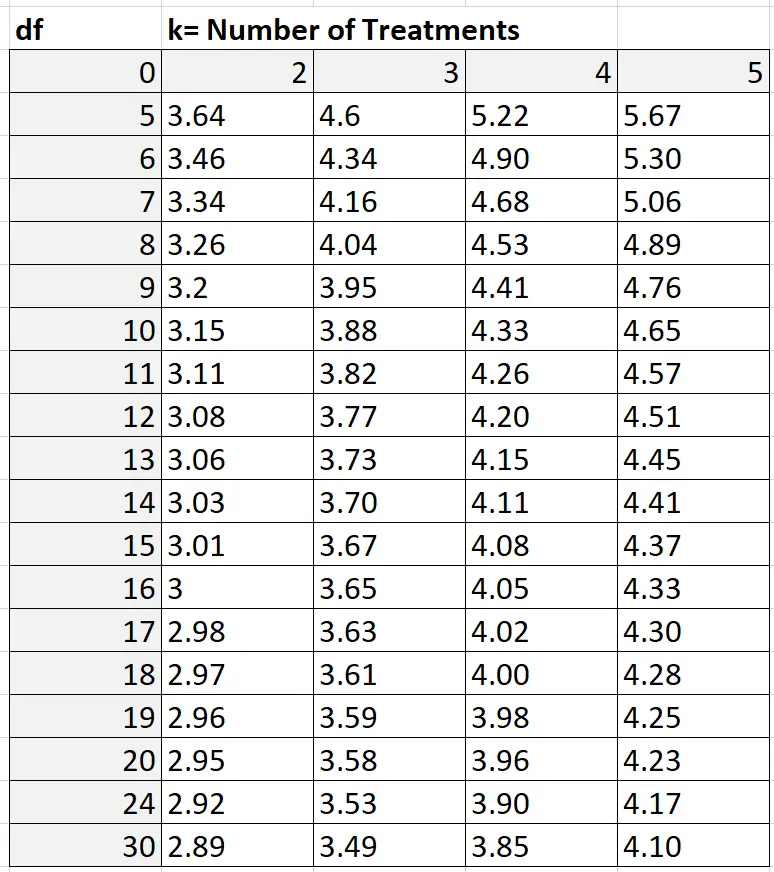
ကျွန်ုပ်တို့၏ဥပမာတွင်၊ k = အုပ်စုအရေအတွက်၊ ဆိုလိုသည်မှာ k = 3။ လွတ်လပ်မှုဒီဂရီများကို nk = 30 – 3 = 27 အဖြစ် တွက်ချက်ထားသည်။ 27 ကို အထက်ဇယားတွင် မဖော်ပြထားသောကြောင့်၊ ကျွန်ုပ်တို့သည် ရှေးရိုးဆန်သော ခန့်မှန်းချက် 24 ကို သုံးနိုင်သည်။ . k = 3 နှင့် df = 24 ကိုအခြေခံ၍ Q = 3.53 ကိုကျွန်ုပ်တို့တွေ့ရှိရပါသည်။

ပေါင်းစည်းထားသောကွဲလွဲမှုကို 19.056 အဖြစ် ထွက်လာသည့် အုပ်စုများ၏ ကွဲပြားမှုများ၏ ပျမ်းမျှအဖြစ် တွက်ချက်နိုင်သည်။

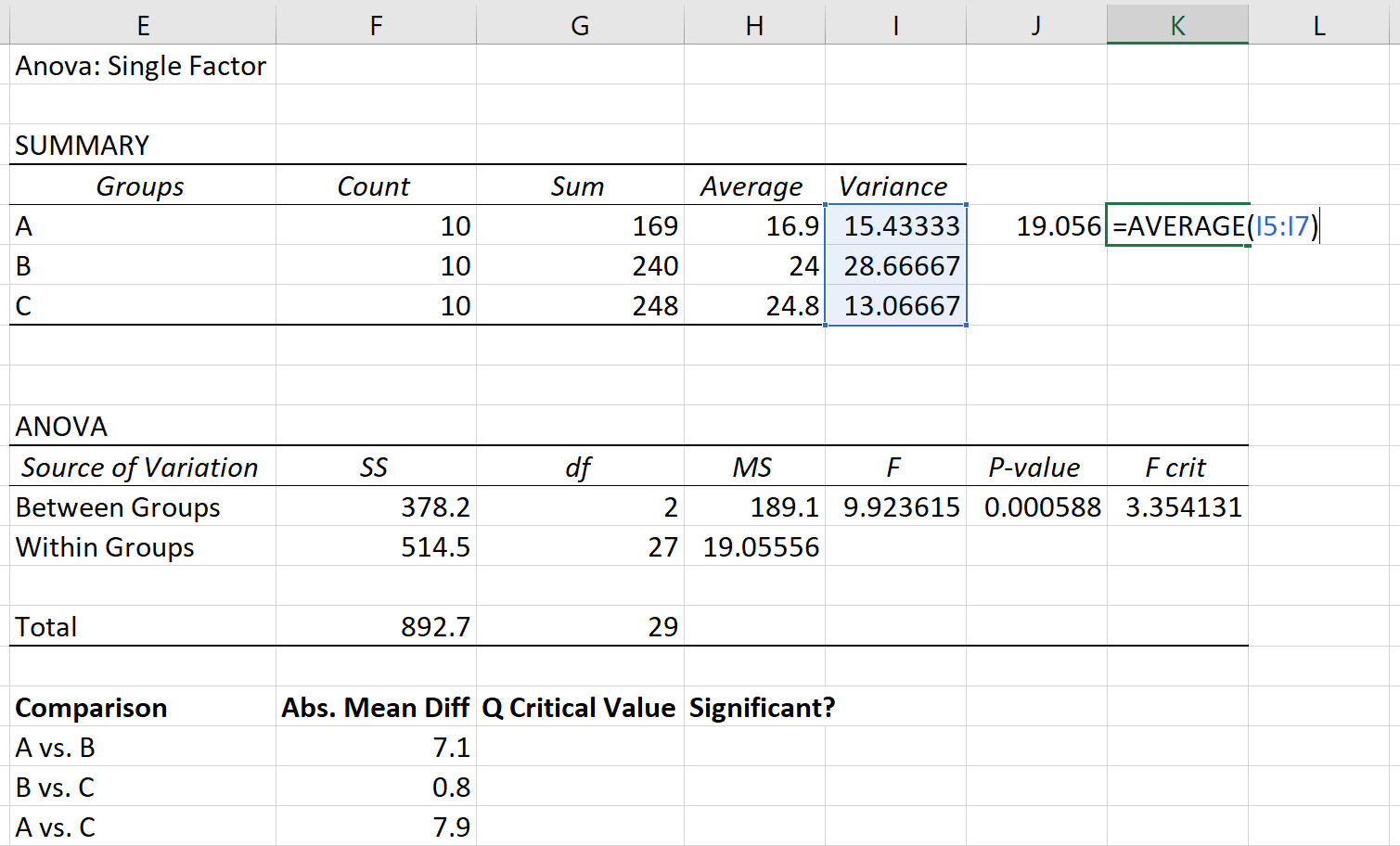
နောက်ဆုံးတွင်၊ အုပ်စုတစ်ခုစီ၏နမူနာအရွယ်အစားမှာ 10 ဖြစ်သည်။

ထို့ကြောင့် ကျွန်ုပ်တို့၏ အရေးကြီးသောတန်ဖိုး Q ကို အောက်ပါအတိုင်း တွက်ချက်နိုင်ပါသည်။

အရေးပါသောတန်ဖိုး Q = Q*√(s ² _{အုပ်စုဖွဲ့ထားသည်} / n.) = 3.53*√(19.056/10) = 4.87 ။

အဆင့် 3- မည်သည့်အဖွဲ့၏ အဓိပ္ပါယ်သည် ကွဲပြားသည်ကို ဆုံးဖြတ်ပါ ။

နောက်ဆုံးတွင်၊ အုပ်စုတစ်ခုစီကြားရှိ ပကတိပျမ်းမျှခြားနားချက်ကို ဝေဖန်ပိုင်းခြားသည့်တန်ဖိုး Q နှင့် နှိုင်းယှဉ်နိုင်ပါသည်။ အကြွင်းမဲ့ဆိုလိုမှုကွာခြားချက်သည် အရေးကြီးသောတန်ဖိုး Q ထက်ကြီးပါက၊ အုပ်စုဆိုလိုသည်များကြားကွာခြားချက်မှာ ကိန်းဂဏန်းအရ သိသာထင်ရှားသည်-

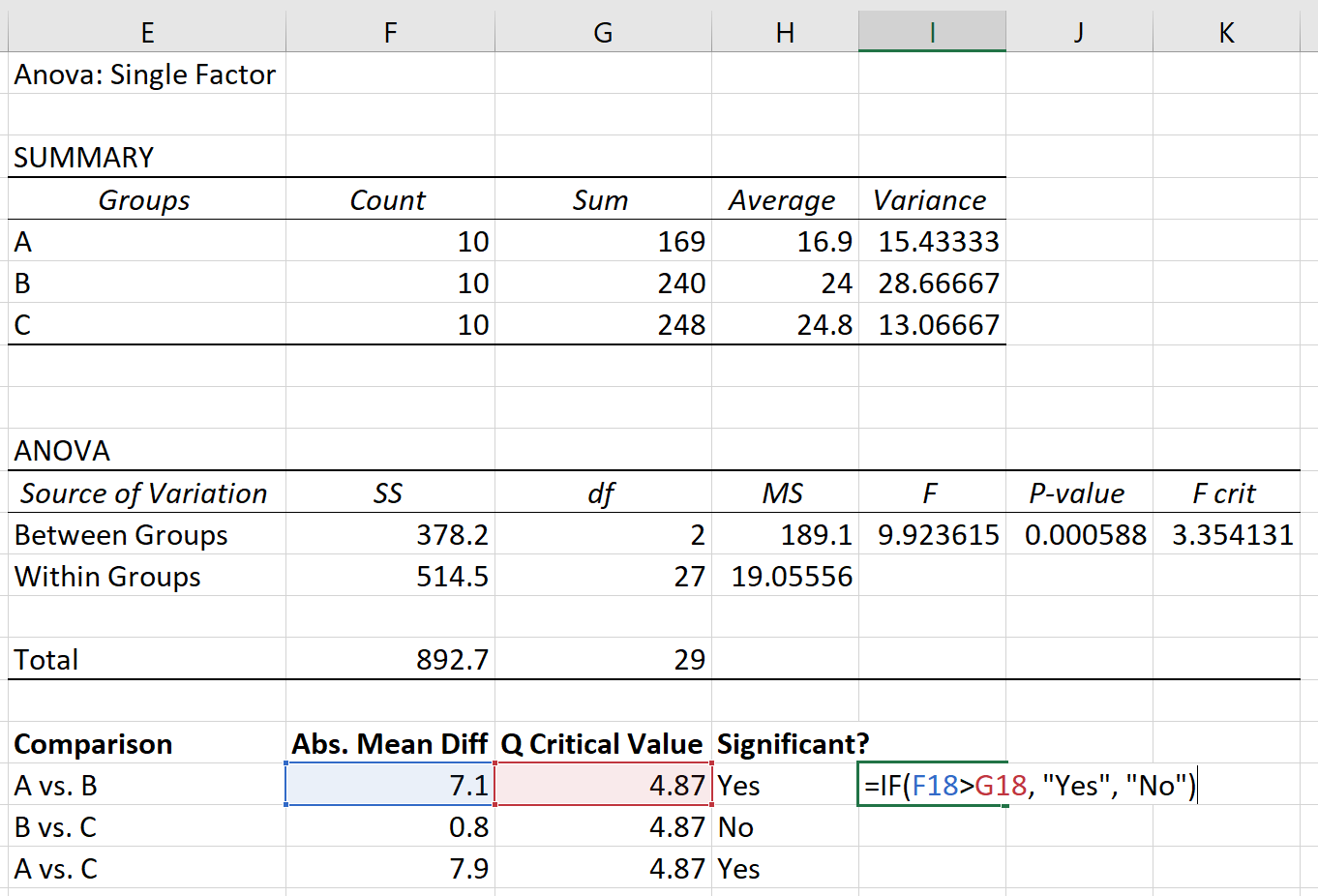
Tukey-Kramer post hoc စာမေးပွဲကို အခြေခံ၍ အောက်ပါတို့ကို တွေ့ရှိရပါသည်။

• အုပ်စု A နှင့် အုပ်စု B အကြား ခြားနားချက်မှာ စာရင်းအင်းအရ သိသာထင်ရှားပါသည်။
• အုပ်စု B နှင့် အုပ်စု C အကြား ခြားနားချက်မှာ စာရင်းအင်းအရ သိသာထင်ရှားခြင်း မရှိပါ ။
• အုပ်စု A နှင့် အုပ်စု C အကြား ခြားနားချက်မှာ စာရင်းအင်းအရ သိသာထင်ရှားပါသည်။

ထပ်လောင်းအရင်းအမြစ်များ

Excel တွင် One-Way ANOVA လုပ်ဆောင်နည်း
ANOVA ဖြင့် Post-Hoc Testing ကိုအသုံးပြုခြင်းလမ်းညွှန်