R တွင် tukey စမ်းသပ်နည်း

တစ်လမ်းသွား ANOVA ကို သုံးသော သို့မဟုတ် ထို့ထက်ပိုသော လွတ်လပ်သော အုပ်စုများအကြား စာရင်းအင်းဆိုင်ရာ သိသာထင်ရှားသော ခြားနားမှု ရှိ၊ မရှိ ဆုံးဖြတ်ရန် အသုံးပြုသည်။

ANOVA ဇယား၏ စုစုပေါင်း p-value သည် အချို့သော အရေးပါမှုအဆင့်အောက်တွင် ရှိနေပါက၊ အနည်းဆုံး အုပ်စု၏ ဆိုလိုရင်းမှာ အခြားနည်းများနှင့် ကွဲပြားသည်ဟု ဆိုရန် လုံလောက်သော အထောက်အထားရှိသည်။

သို့သော် မည်သည့် အဖွဲ့များ အချင်းချင်း ကွဲပြားသည်ကို ဤအရာက ကျွန်ုပ်တို့အား မပြောပါ။ ၎င်းသည် ကျွန်ုပ်တို့အား အုပ်စု ပျမ်းမျှ ပျမ်းမျှအားလုံး မညီမျှကြောင်း ရိုးရှင်းစွာ ပြောပြသည်။ ဘယ်အဖွဲ့တွေက တစ်ခုနဲ့တစ်ခု မတူဘူးဆိုတာ အတိအကျသိဖို့အတွက် post hoc test လုပ်ဖို့လိုပါတယ်။

အသုံးအများဆုံး post hoc စာမေးပွဲများထဲမှ တစ်ခုသည် Tukey test ဖြစ်သည်၊ ၎င်းသည် မိသားစုအလိုက် အမှားအယွင်းနှုန်းကို ထိန်းချုပ်နေစဉ် အုပ်စုတစ်ခုစီ၏ နည်းလမ်းများကြားတွင် pairwise နှိုင်းယှဉ်မှုများကို လုပ်ဆောင်နိုင်စေပါသည်။

ဤသင်ခန်းစာတွင် Tukey စာမေးပွဲကို R တွင် မည်သို့လုပ်ဆောင်ရမည်ကို ရှင်းပြထားသည်။

မှတ်ချက်- သင့်လေ့လာမှုရှိအဖွဲ့များကို ထိန်းချုပ်သည့်အဖွဲ့ဟုယူဆပါက၊ Dunnett ၏စမ်းသပ်မှုကို post-hoc စမ်းသပ်မှုအဖြစ် သင်အသုံးပြုသင့်သည်။

ဥပမာ- R တွင် Tukey စမ်းသပ်မှု

အဆင့် 1- ANOVA မော်ဒယ်ကို အံကိုက်လုပ်ပါ။

အောက်ပါကုဒ်သည် အုပ်စုသုံးစု (A၊ B၊ နှင့် C) ဖြင့် ဒေတာအတုအစုံကို ဖန်တီးနည်းကို ပြသပြီး အုပ်စုတစ်ခုစီ၏ ပျမ်းမျှတန်ဖိုးများ တူညီခြင်းရှိမရှိ ဆုံးဖြတ်ရန် တစ်ကြောင်း ANOVA မော်ဒယ်ကို ဒေတာနှင့် အံဝင်ခွင်ကျဖြစ်စေသည်-

 #make this example reproducible
set.seed(0)

#create data
data <- data.frame(group = rep (c("A", "B", "C"), each = 30),
                   values = c(runif(30, 0, 3),
                                   runif(30, 0, 5),
                                   runif(30, 1, 7)))

#view first six rows of data
head(data)

  group values
1 A 2.6900916
2 A 0.7965260
3 A 1.1163717
4 A 1.7185601
5 A 2.7246234
6 A 0.6050458

#fit one-way ANOVA model
model <- aov (values~group, data=data)

#view the model output
summary(model)

            Df Sum Sq Mean Sq F value Pr(>F)    
group 2 98.93 49.46 30.83 7.55e-11 ***
Residuals 87 139.57 1.60                     
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

ANOVA ဇယားမှ အလုံးစုံ p-တန်ဖိုးသည် 7.55e-11 ဖြစ်ကြောင်း ကျွန်ုပ်တို့ တွေ့နိုင်ပါသည်။ ဤကိန်းဂဏန်းသည် 0.05 ထက်နည်းသောကြောင့်၊ အုပ်စုတစ်ခုစီရှိ ပျမ်းမျှတန်ဖိုးများသည် မညီမျှကြောင်းပြောရန် လုံလောက်သော အထောက်အထားရှိသည်။ ထို့ကြောင့်၊ မည်သည့်အဖွဲ့၏ အဓိပ္ပါယ်သည် ကွဲပြားသည်ကို အတိအကျ ဆုံးဖြတ်ရန် Tukey test ကို ပြုလုပ်နိုင်ပါသည်။

အဆင့် 2: Tukey စမ်းသပ်မှုကို လုပ်ဆောင်ပါ။

Tukey စမ်းသပ်မှုကို လုပ်ဆောင်ရန် အောက်ပါကုဒ်သည် TukeyHSD() လုပ်ဆောင်ချက်ကို အသုံးပြုနည်းကို ပြသသည်-

 #perform Tukey's Test
TukeyHSD(model, conf.level= .95 ) 

  Tukey multiple comparisons of means
    95% family-wise confidence level

Fit: aov(formula = values ~ group, data = data)

$group
         diff lwr upr p adj
BA 0.9777414 0.1979466 1.757536 0.0100545
CA 2.5454024 1.7656076 3.325197 0.0000000
CB 1.5676610 0.7878662 2.347456 0.0000199

p-value သည် ပရိုဂရမ်တစ်ခုစီကြားတွင် စာရင်းအင်းဆိုင်ရာ သိသာထင်ရှားသော ခြားနားချက်ရှိမရှိကို ဖော်ပြသည်။ ရလဒ်များက 0.05 အရေးပါမှုအဆင့်တွင် ပရိုဂရမ်တစ်ခုစီ၏ ပျမ်းမျှကိုယ်အလေးချိန် လျော့ကျမှုကြားတွင် ကိန်းဂဏန်းသိသိသာသာ ကွာခြားမှုရှိကြောင်း ပြသသည်။

အထူးသဖြင့်-

• B နှင့် A အကြားခြားနားချက်အတွက် P တန်ဖိုး: 0.0100545
• P တန်ဖိုးသည် C နှင့် A အကြား ခြားနားချက် 0.0000000 ဖြစ်သည်။
• C နှင့် B အကြားခြားနားချက်အတွက် P တန်ဖိုး: 0.0000199

အဆင့် 3- ရလဒ်များကို မြင်ယောင်ကြည့်ပါ။

ယုံကြည်မှုကြားကာလများကို မြင်သာစေရန် plot(TukeyHSD()) လုပ်ဆောင်ချက်ကိုလည်း အသုံးပြုနိုင်ပါသည်။

 #plot confidence intervals
plot(TukeyHSD(model, conf.level= .95 ), las = 2 )

မှတ်ချက် ။

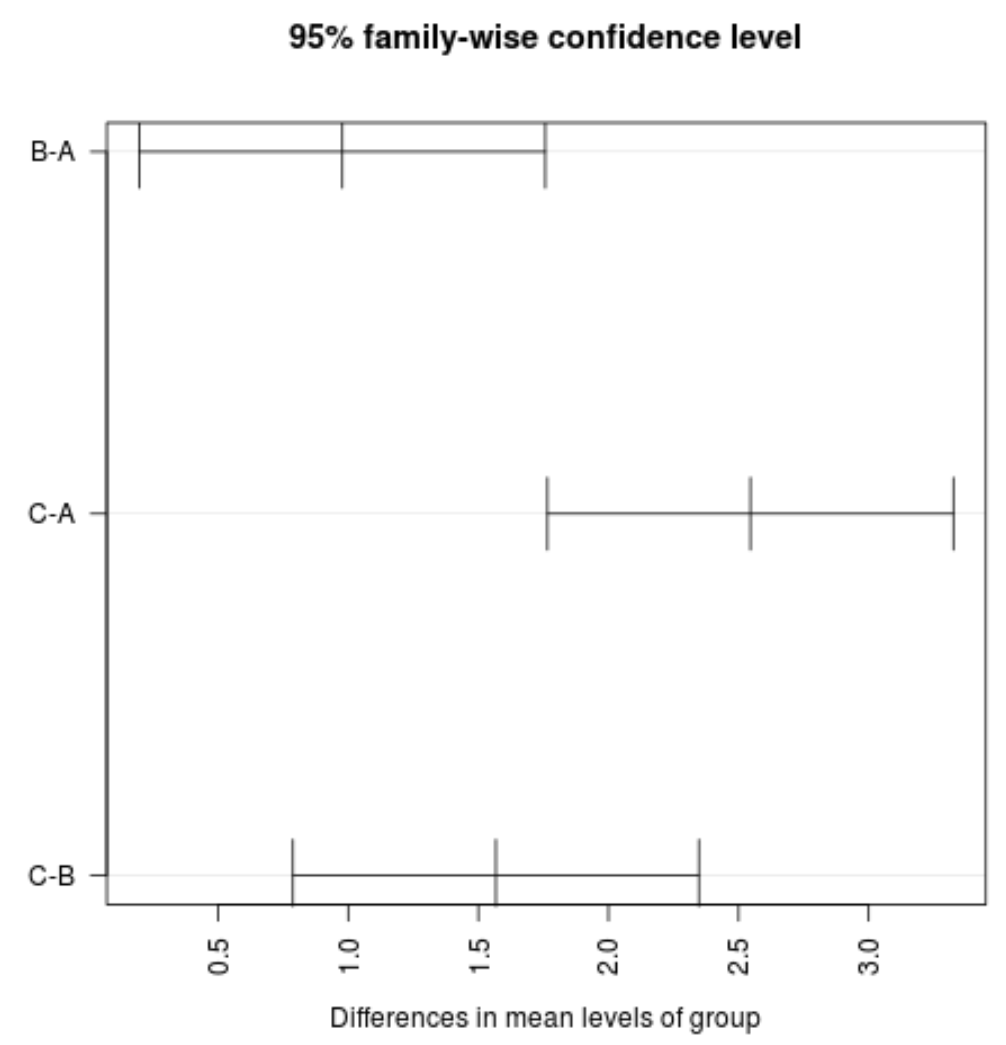
အဖွဲ့များကြားရှိ ပျမ်းမျှတန်ဖိုးအတွက် ယုံကြည်မှုကြားကာလတစ်ခုမှ တန်ဖိုးသုညမပါဝင်ကြောင်း ကျွန်ုပ်တို့တွေ့မြင်နိုင်သည်၊ အုပ်စုသုံးစုကြား ပျမ်းမျှဆုံးရှုံးမှုတွင် စာရင်းအင်းအရ သိသာထင်ရှားသော ကွာခြားချက်ရှိကြောင်း ကျွန်ုပ်တို့မြင်နိုင်သည်။ ၎င်းသည် ကျွန်ုပ်တို့၏ယူဆချက်စမ်းသပ်မှုများအတွက် 0.05 ထက်နည်းသော p-တန်ဖိုးများအားလုံးနှင့် ကိုက်ညီပါသည်။

ဤအထူးဥပမာအတွက်၊ ကျွန်ုပ်တို့ အောက်ပါအတိုင်း ကောက်ချက်ချနိုင်သည်-

• အုပ်စု C ၏ ပျမ်းမျှတန်ဖိုးများသည် အုပ်စု A နှင့် B တို့၏ ပျမ်းမျှတန်ဖိုးများထက် သိသိသာသာမြင့်မားသည်။
• အုပ်စု B ၏ပျမ်းမျှတန်ဖိုးများသည် အုပ်စု A ၏ပျမ်းမျှတန်ဖိုးများထက် သိသိသာသာမြင့်မားသည်။

ထပ်လောင်းအရင်းအမြစ်များ

ANOVA ဖြင့် Post-Hoc Testing ကိုအသုံးပြုခြင်းလမ်းညွှန်
တစ်လမ်းမောင်း ANOVA ကို R ဖြင့် မည်သို့လုပ်ဆောင်ရမည်နည်း။
R ဖြင့် နှစ်လမ်းသွား ANOVA ကို မည်သို့လုပ်ဆောင်ရမည်နည်း။