တူကီး vs. ဘွန်ဖာရိုနီ vs. scheffe – ဘယ်စမ်းသပ်မှုကို သင်အသုံးပြုသင့်သလဲ။

တစ်လမ်းသွား ANOVA ကို သုံးသော သို့မဟုတ် ထို့ထက်ပိုသော လွတ်လပ်သော အုပ်စုများကြားတွင် စာရင်းအင်းဆိုင်ရာ သိသာထင်ရှားသော ခြားနားမှု ရှိ၊ မရှိ ဆုံးဖြတ်ရန် အသုံးပြုသည်။

ANOVA ဇယား၏ စုစုပေါင်း p-value သည် အချို့သော အရေးပါမှုအဆင့်အောက်တွင် ရှိနေပါက၊ အနည်းဆုံး အုပ်စု၏ ဆိုလိုရင်းမှာ အခြားနည်းများနှင့် ကွဲပြားသည်ဟု ဆိုရန် လုံလောက်သော အထောက်အထားရှိသည်။

သို့သော် မည်သည့် အဖွဲ့များ အချင်းချင်း ကွဲပြားသည်ကို ဤအရာက ကျွန်ုပ်တို့အား မပြောပါ။ ၎င်းသည် ကျွန်ုပ်တို့အား အုပ်စု ပျမ်းမျှ ပျမ်းမျှအားလုံး မညီမျှကြောင်း ရိုးရှင်းစွာ ပြောပြသည်။

ဘယ်အဖွဲ့တွေက တစ်ခုနဲ့တစ်ခု မတူဘူးဆိုတာ အတိအကျသိနိုင်ဖို့၊ မိသားစုအလိုက် အမှားအယွင်းနှုန်းကို ထိန်းချုပ်နိုင်တဲ့ Post-hoc စမ်းသပ်မှုကို လုပ်ဆောင်ဖို့ လိုပါတယ်။

အသုံးအများဆုံး post-hoc စမ်းသပ်မှု သုံးခုတွင်-

• Tukey နည်းလမ်း
• Scheffe နည်းလမ်း
• Bonferroni နည်းလမ်း

ဤသင်ခန်းစာသည် နည်းလမ်းတစ်ခုစီ၏ ခြုံငုံသုံးသပ်ချက်အပြင် အခြေအနေပေါ်မူတည်၍ မည်သည့် post-hoc စာမေးပွဲကို အသုံးပြုရမည်နည်း။

Tukey နည်းလမ်း

အုပ်စုတစ်ခုစီ၏နမူနာအရွယ်အစားသည် တူညီသောအခါတွင် Tukey ၏ post hoc စာမေးပွဲကို အုပ်စုများကြားတွင် pairwise နှိုင်းယှဉ်မှုများပြုလုပ်လိုသောအခါတွင် အသုံးပြုသင့်သည်။

နမူနာအရွယ်အစားများ မ ညီပါက၊ Tukey-Kramer စမ်းသပ်မှုဟု လူသိများသော စမ်းသပ်မှု၏ မွမ်းမံထားသောဗားရှင်းကို သင်အသုံးပြုနိုင်ပါသည်။

“ pairwise” ဟူသောအသုံးအနှုန်းသည် တစ်ကြိမ်လျှင် အုပ်စုနှစ်စု၏ အဓိပ္ပါယ်ကို နှိုင်းယှဉ်လိုပါသည်။

ဥပမာအားဖြင့်၊ ကျွန်ုပ်တို့တွင် A၊ B၊ C အုပ်စုသုံးစုရှိသည်ဆိုပါစို့။

Tukey ၏ post-hoc စာမေးပွဲသည် ကျွန်ုပ်တို့အား အောက်ပါအတွဲလိုက် နှိုင်းယှဉ်မှုများကို ပြုလုပ်နိုင်စေသည်-

• _µA = _µB
• _µA = _µC
• _μB = _μC

k အုပ်စုများအတွက် စုစုပေါင်း k ( k -1)/2 ဖြစ်နိုင်ချေရှိသော အတွဲလိုက် နှိုင်းယှဉ်မှုများ ရှိနေသည်ကို သတိပြုပါ။

Scheffe နည်းလမ်း

Scheffe post-hoc စာမေးပွဲကို အဖွဲ့ဟူသည်တို့ကြား ဖြစ်နိုင်ချေရှိသော ဆန့်ကျင်ဘက် အားလုံးကို ပြုလုပ်လိုသောအခါတွင် အသုံးပြုသင့်သည်။ ဤစစ်ဆေးမှုသည် Tukey post-hoc စာမေးပွဲနှင့်မတူဘဲ တစ်ကြိမ်လျှင် နည်းလမ်းနှစ်ခုထက်ပို၍ နှိုင်းယှဉ်နိုင်စေပါသည်။

ဥပမာအားဖြင့်၊ ကျွန်ုပ်တို့တွင် A, B, C, D အုပ်စုလေးခုရှိသည်ဆိုပါစို့။

Scheffe post-hoc စမ်းသပ်မှုသည် ရှုပ်ထွေးသော နှိုင်းယှဉ်မှုများကို ပြုလုပ်နိုင်စေသည်-

• _μA – _μB = _μC – _μD
• _μA + _μD = _μB + _μC

Scheffe post hoc test သည် လိုက်လျောညီထွေ အရှိဆုံးဖြစ်သော်လည်း၊ ၎င်းသည် ရှေးရိုးဆန်ဆုံးဖြစ်ပြီး အကျယ်ဆုံးယုံကြည်မှုကြားကာလကို ထုတ်ပေးသည်။ ဆိုလိုသည်မှာ ၎င်းတွင် အနိမ့်ဆုံး စာရင်းအင်းဆိုင်ရာ ပါဝါနှင့် အုပ်စုများကြား စစ်မှန်သော ခြားနားချက်များကို ရှာဖွေနိုင်မှု အနိမ့်ဆုံး စွမ်းရည်ရှိသည်။

Scheffe post-hoc စစ်ဆေးမှုသည် အုပ်စုနမူနာအရွယ်အစားများ တူညီမှုရှိ/မရှိကို အသုံးပြုနိုင်ကြောင်း သတိပြုပါ။

Bonferroni နည်းလမ်း

ကြိုတင် စီစဉ်ထားသော နှိုင်းယှဉ်မှုအစုအဝေးကို လုပ်ဆောင်လိုသည့်အခါ Bonferroni Post-hoc စမ်းသပ်မှုကို အသုံးပြုသင့်သည်။

ဥပမာအားဖြင့်၊ ကျွန်ုပ်တို့တွင် အုပ်စုသုံးစု – A, B, C – ရှိသည်ဆိုပါစို့၊ ကျွန်ုပ်တို့သည် အောက်ပါနှိုင်းယှဉ်ချက်များကိုသာ စိတ်ဝင်စားကြောင်း ကြိုသိပါသည်။

• _µA = _µB
• _μB = _μC

ကျွန်ုပ်တို့တွင် ဤကဲ့သို့သောကြိုတင်လုပ်ဆောင်လိုသည့် နှိုင်းယှဉ်မှုအစီအစဥ်တစ်ခုရှိသောအခါ၊ Bonferroni post hoc test သည် အကျဉ်းဆုံးသောယုံကြည်မှုကြားကာလများကို ထုတ်လုပ်ပေးသည်၊ ဆိုလိုသည်မှာ ၎င်းသည် အကျိုးစီးပွားအုပ်စုများကြားတွင် စစ်မှန်သောခြားနားချက်ကို ရှာဖွေတွေ့ရှိရန် အကြီးမားဆုံးစွမ်းရည်ရှိသည်။ .

Bonferroni post-hoc test သည် အုပ်စုနမူနာအရွယ်အစားများ တူညီမှုရှိမရှိကိုလည်း အသုံးပြုနိုင်ကြောင်း သတိပြုပါ။

ဘယ်နည်းလမ်းကို သုံးသင့်လဲ။

အောက်ပါဆုံးဖြတ်ချက်သစ်ပင်သည် အခြေအနေပေါ်မူတည်၍ မည်သည့် post-hoc စာမေးပွဲကို အသုံးပြုသင့်သည်ကို ဆုံးဖြတ်ရန် ကူညီပေးသည်-

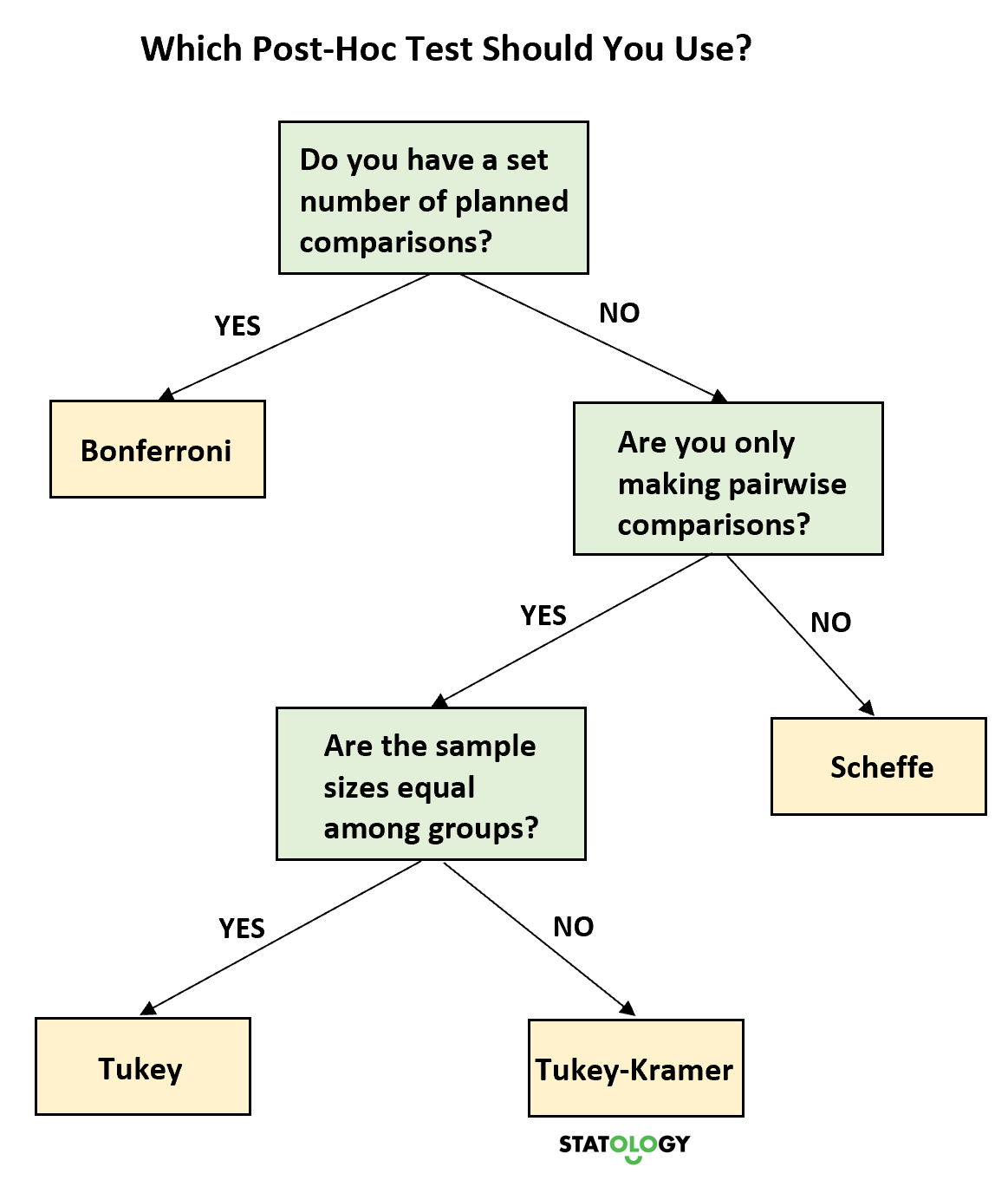
နောက်ဆုံးအတွေးများ

မည်သည့် post-hoc စာမေးပွဲကို သင်အသုံးပြုရန် ရွေးချယ်သည်၊ စမ်းသပ်မှုကို မလုပ်ဆောင် မီ သင်ဆုံးဖြတ်ရပါမည်။

၎င်းသည် မရိုးသားသော သုတေသနလုပ်ထုံးလုပ်နည်းဟု ယူဆထားသည့် သိသာထင်ရှားသောရလဒ်များထွက်လာနိုင်ခြေပိုများမည့် စမ်းသပ်မှုအပြီးတွင် လွန်ကဲစမ်းသပ်မှုတစ်ခုကို ရွေးချယ်ခြင်းမှ သင့်ကို တားဆီးထားသည်။

မည်သို့ပင်ဆိုစေကာမူ၊ စာရင်းအင်းဆော့ဖ်ဝဲအများစုသည် ဤ post-hoc စမ်းသပ်မှုများကို လုပ်ဆောင်နိုင်စွမ်းရှိသောကြောင့် ၎င်းတို့ကို ကိုယ်တိုင်တွက်ချက်ရန် ခဲယဉ်းပေလိမ့်မည်။