ပုံမှန်မဟုတ်သော ဖြန့်ဖြူးခြင်းဆိုသည်မှာ အဘယ်နည်း။ (အဓိပ္ပါယ် & #038; ဥပမာ)
unimodal distribution သည် ရှင်းရှင်းလင်းလင်း အထွတ်အထိပ်ဖြင့် ဖြစ်နိုင်ခြေ ဖြန့်ဖြူးမှုဖြစ်သည်။
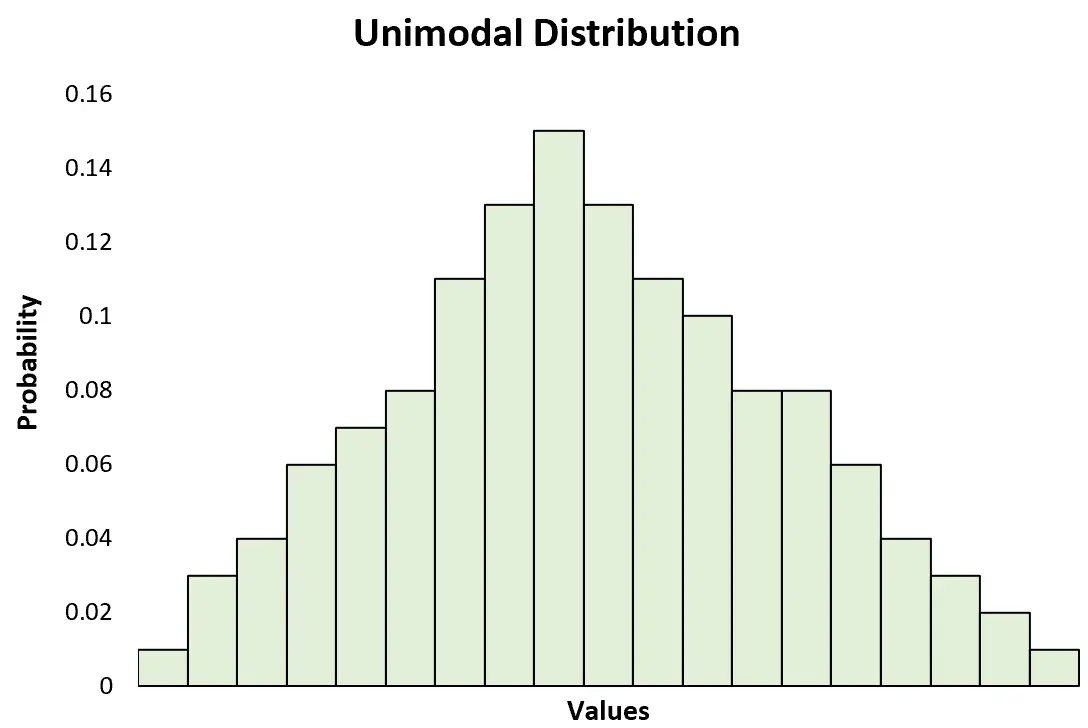
၎င်းသည် ရှင်းလင်းသော အထွတ်အထိပ်နှစ်ခုပါရှိသော bimodal distribution နှင့် ဆန့်ကျင်ဘက်ဖြစ်သည်။
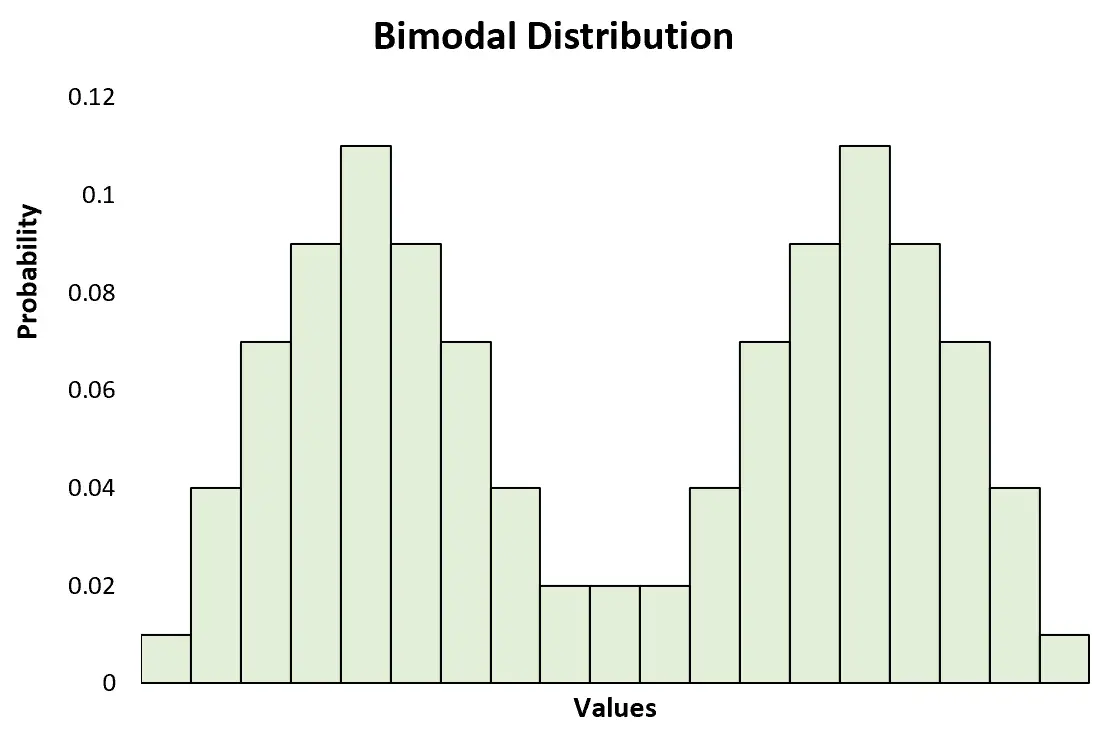
၎င်းသည် အထွတ်အထိပ် နှစ်ခု သို့မဟုတ် ထို့ထက်ပိုသော ဘက်စုံဖြန့်ဖြူးမှု တစ်ခုနှင့်လည်း ဆန့်ကျင်ဘက်ဖြစ်သည်-
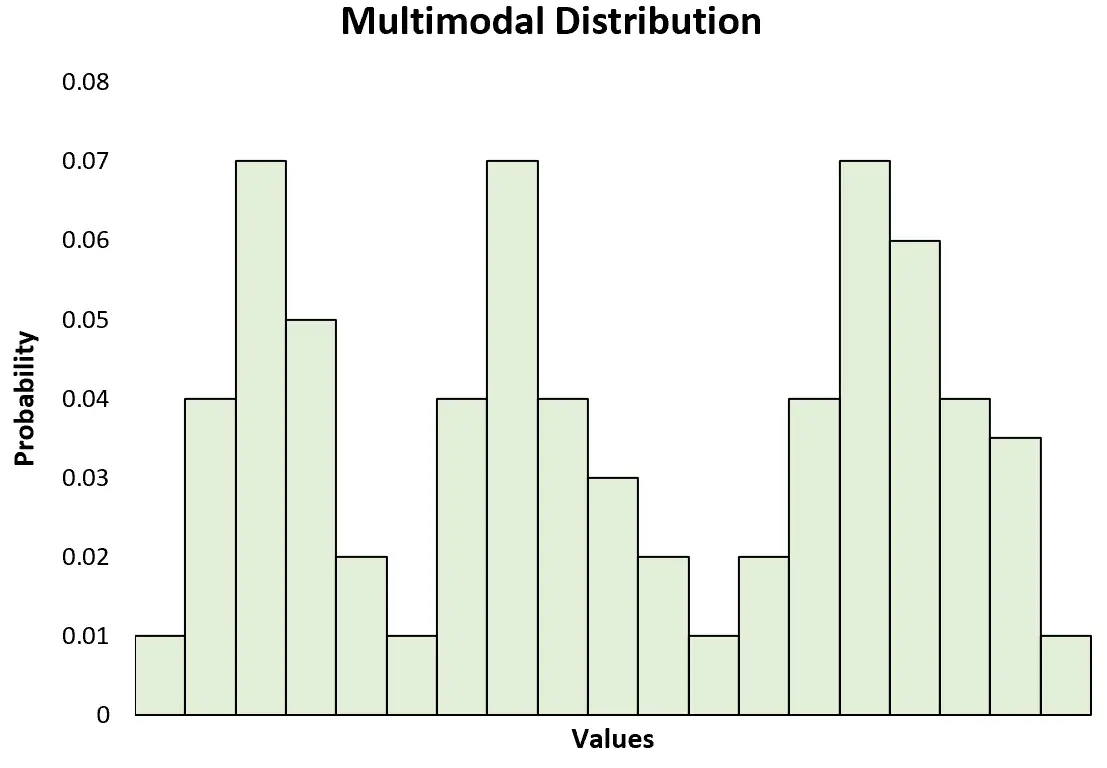
မှတ်ချက်- bimodal ဖြန့်ဖြူးမှုသည် သီးခြား ဘက်စုံဖြန့်ဖြူးမှု အမျိုးအစားတစ်ခုမျှသာ ဖြစ်သည်။
ပုံမှန်မဟုတ်သော ဖြန့်ဝေမှုများ၏ ဥပမာများ
ဤသည်မှာ လက်တွေ့တွင် ပုံမှန်မဟုတ်သော ဖြန့်ဝေမှုများ၏ ဥပမာအချို့ဖြစ်သည်။
ဥပမာ 1- မွေးကင်းစကလေးများ၏အလေးချိန်
မွေးကင်းစကလေးများ၏ ကိုယ်အလေးချိန် ဖြန့်ဝေမှုသည် ပျမ်းမျှအားဖြင့် 7.5 ပေါင်ဝန်းကျင်ဖြင့် ပုံမှန်မဟုတ်သော ဖြန့်ဝေမှုနောက်ဆက်တွဲဖြစ်ကြောင်း ကောင်းစွာသိရှိထားသည်။ ကျွန်ုပ်တို့သည် ကလေးများ၏ ကိုယ်အလေးချိန်၏ ဟီစတိုဂရမ်ကို ဖန်တီးပါက၊ အချို့ကလေးငယ်များသည် ကိုယ်အလေးချိန်ပိုများပြီး အချို့သောကလေးများသည် ကိုယ်အလေးချိန်နည်းသဖြင့် “ အထွတ်အထိပ်” ကို မြင်တွေ့ရမည်ဖြစ်သည်။

ဥပမာ 2- ACT ရမှတ်များ
အမေရိကန်ပြည်ထောင်စုရှိ အထက်တန်းကျောင်းသူကျောင်းသားများအတွက် ပျမ်းမျှ ACT ရမှတ်သည် 21 ဝန်းကျင်ဖြစ်ပြီး၊ အချို့သောကျောင်းသားများက အမှတ်နိမ့်ကြပြီး အချို့က အမှတ်ပိုများသည်။ အကယ်၍ ကျွန်ုပ်တို့သည် အမေရိကန်ပြည်ထောင်စုရှိ ကျောင်းသားအားလုံးအတွက် ACT ရမှတ်များ၏ ဟီစတိုဂရမ်တစ်ခုကို ဖန်တီးပါက၊ အချို့သော ကျောင်းသားများအတွက် ရမှတ်များ ပိုမိုမြင့်မားပြီး အခြားသူများအတွက် ရမှတ်များ နည်းပါးသည့် အသက် 21 နှစ်တွင် “ အထွတ်အထိပ်” တစ်ခုတည်းကို မြင်တွေ့ရမည်ဖြစ်သည်။
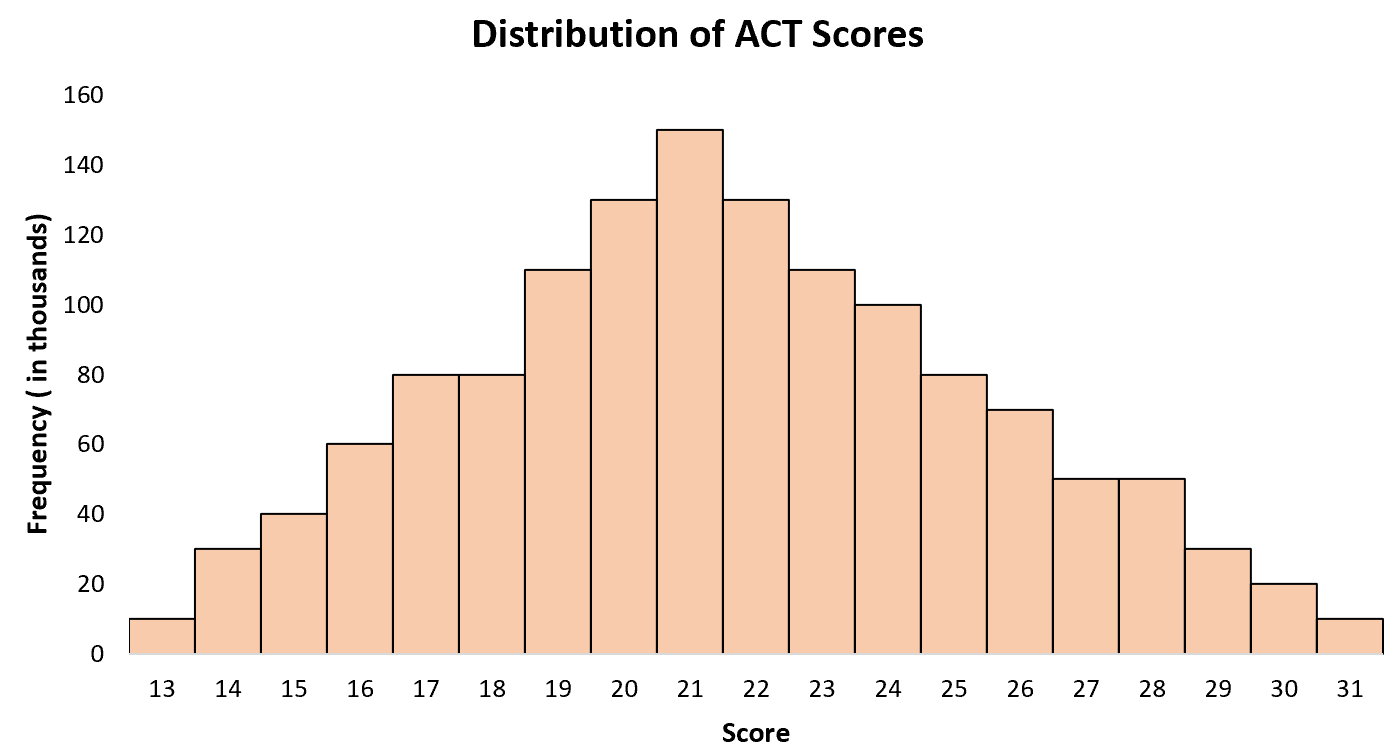
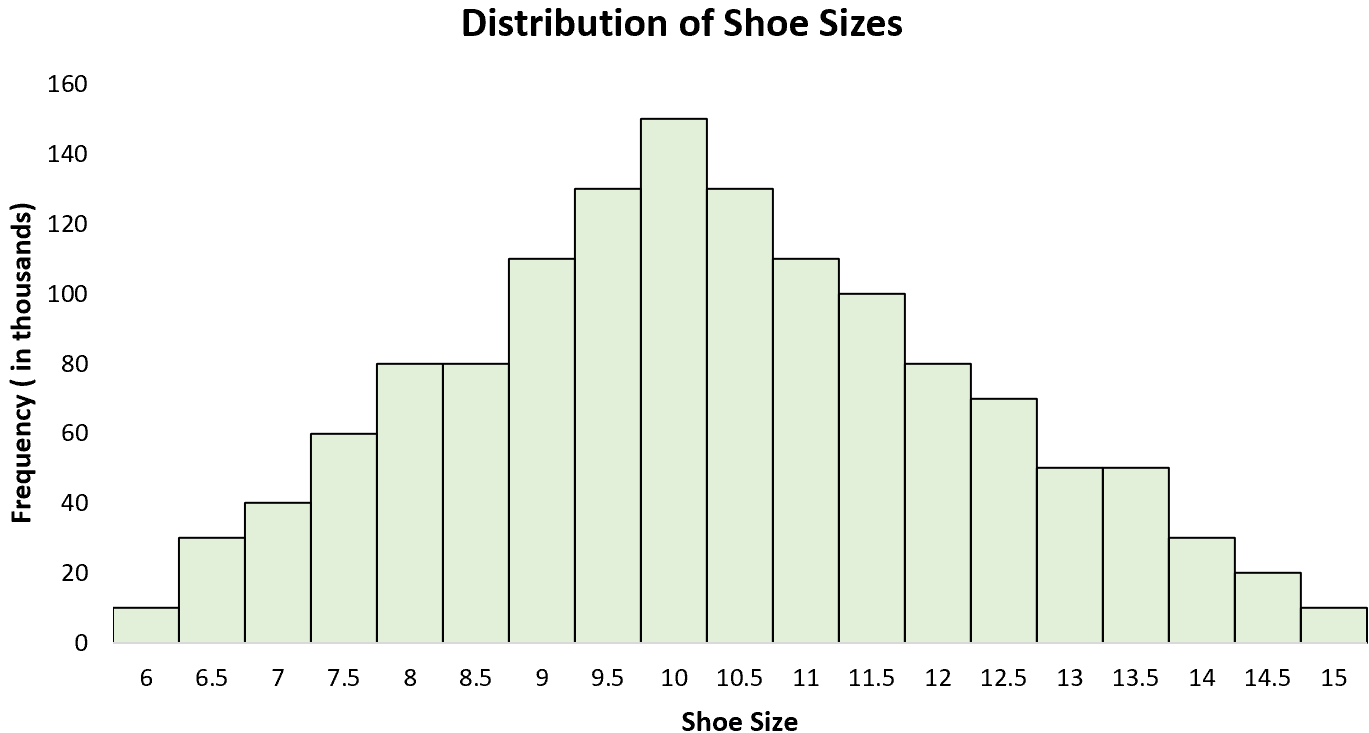
ဥပမာ 3- ဖိနပ်အရွယ်အစား
အမျိုးသားများ၏ ဖိနပ်အရွယ်အစားများကို ဖြန့်ချီခြင်းသည် 10 ဝန်းကျင်တွင် “ အထွတ်အထိပ်” ဖြင့် ပုံမှန်မဟုတ်သော ဖြန့်ဝေမှုဖြစ်သည်။ အမျိုးသားဖိနပ်အရွယ်အစားအားလုံး၏ ဟီစတိုဂရမ်တစ်ခုကို ဖန်တီးပါက 10 တွင် တစ်ခုတည်းသော အထွတ်အထိပ်တစ်ခုကို တွေ့ရမည်ဖြစ်ပြီး ပိုကြီးသောဖိနပ်အရွယ်အစားကို ဝတ်ဆင်ထားသည့် အမျိုးသားအချို့နှင့် အခြားပိုကြီးသောဖိနပ်များကို ၀တ်ဆင်ထားသည်။ အရွယ်အစား။ ပိုသေးငယ်တဲ့အရွယ်အစား။
စာရင်းဇယားများတွင် တူညီသော ဖြန့်ဝေမှုများ
စာရင်းဇယားများတွင် အောက်ပါဖြစ်နိုင်ခြေ ဖြန့်ဝေမှုများသည် စံမညီသော ဖြန့်ဝေမှုများဖြစ်သည်-
ပုံမှန် ဖြန့်ဖြူးမှု
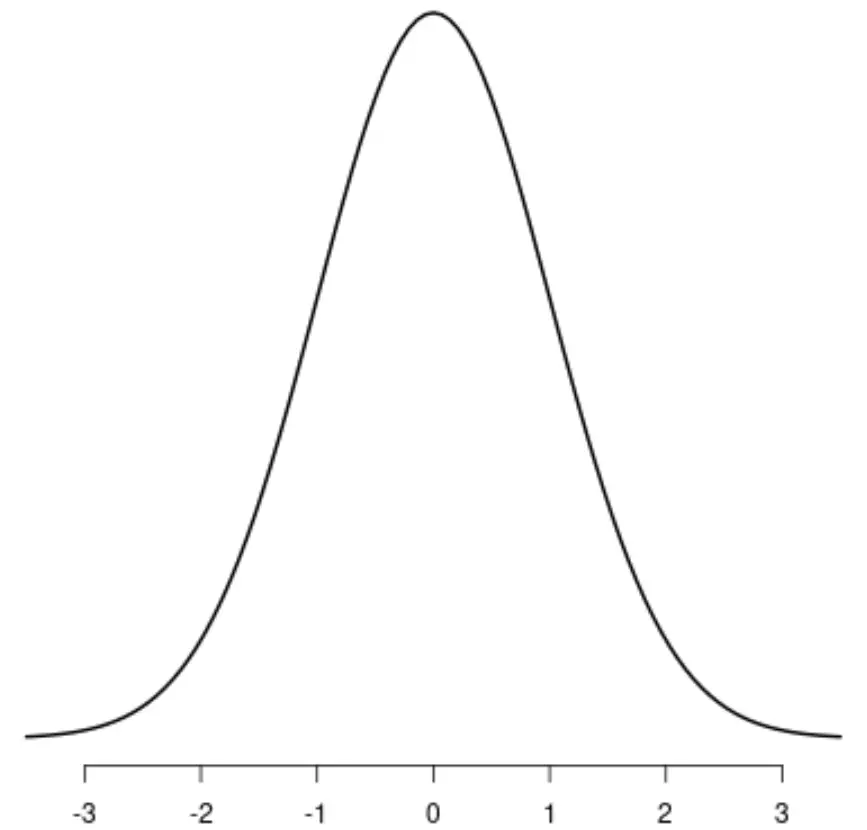
ဖြန့်ချီရေး t
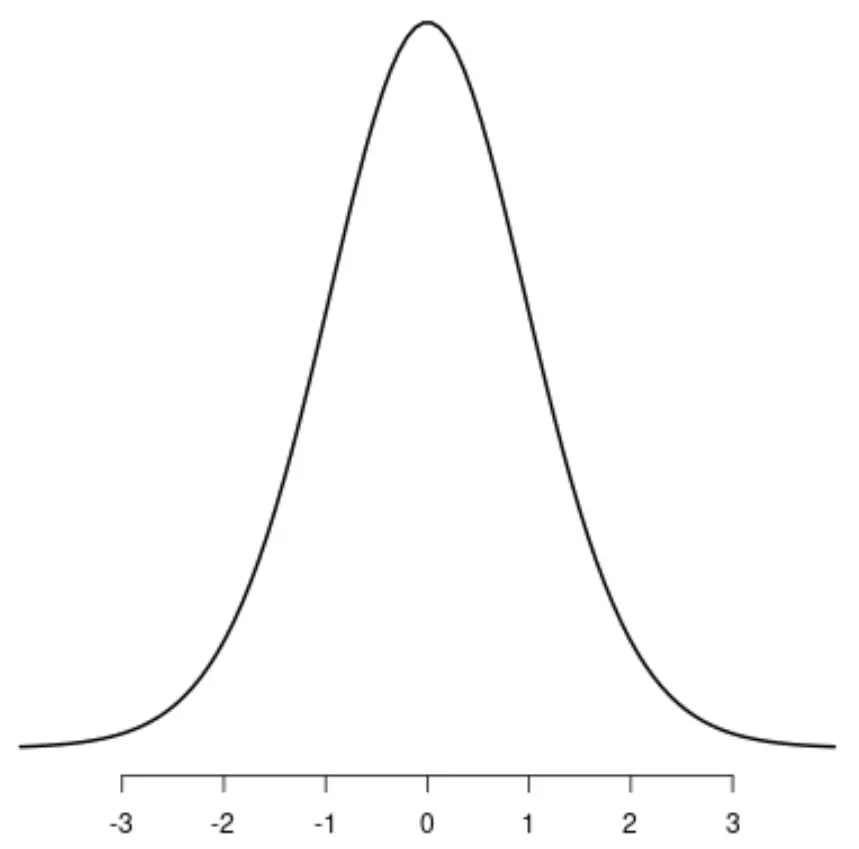
ယူနီဖောင်း ဖြန့်ဖြူးခြင်း။

Cauchy ဖြန့်ဖြူးခြင်း။
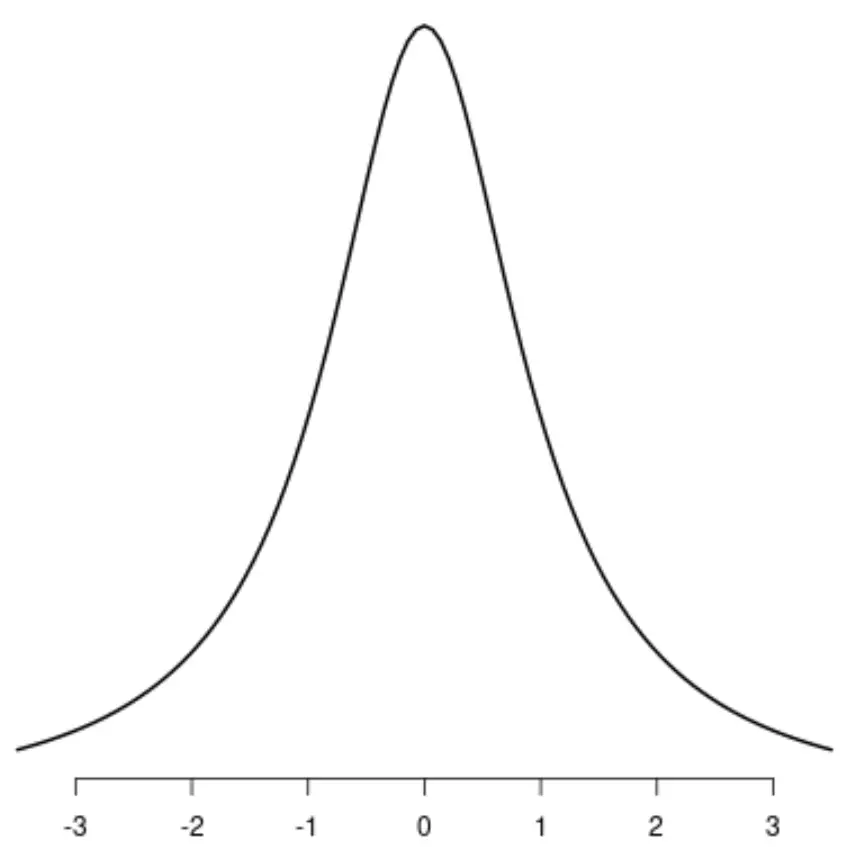
ဤဖြန့်ဝေမှုတစ်ခုစီတွင် ထူးခြားသော အထွတ်အထိပ်တစ်ခုစီ ရှိသည်ကို သတိပြုပါ။
ပုံမှန်မဟုတ်သော ဖြန့်ဖြူးမှုများကို ခွဲခြမ်းစိတ်ဖြာနည်း
ဗဟိုသဘောထားမတူညီသော အတိုင်းအတာ သုံးရပ်ကို အသုံးပြု၍ ပုံမှန်မဟုတ်သော ဖြန့်ဝေမှုများကို ကျွန်ုပ်တို့မကြာခဏဖော်ပြသည်-
- ပျမ်းမျှ : ပျမ်းမျှတန်ဖိုး
- Median : ပျမ်းမျှတန်ဖိုး
- မုဒ် – မကြာခဏပေါ်လာသောတန်ဖိုး
ဖြန့်ဖြူးမှု၏ အချိုးမညီမှု ပေါ်မူတည်၍ ဤတိုင်းတာမှုသုံးခုကို မတူညီသောနေရာများတွင် တွေ့ရှိနိုင်သည်။
ဘယ်ဘက်စောင်း ဖြန့်ချီခြင်း- အဓိပ္ပါယ် < မီဒီယံ < မုဒ်
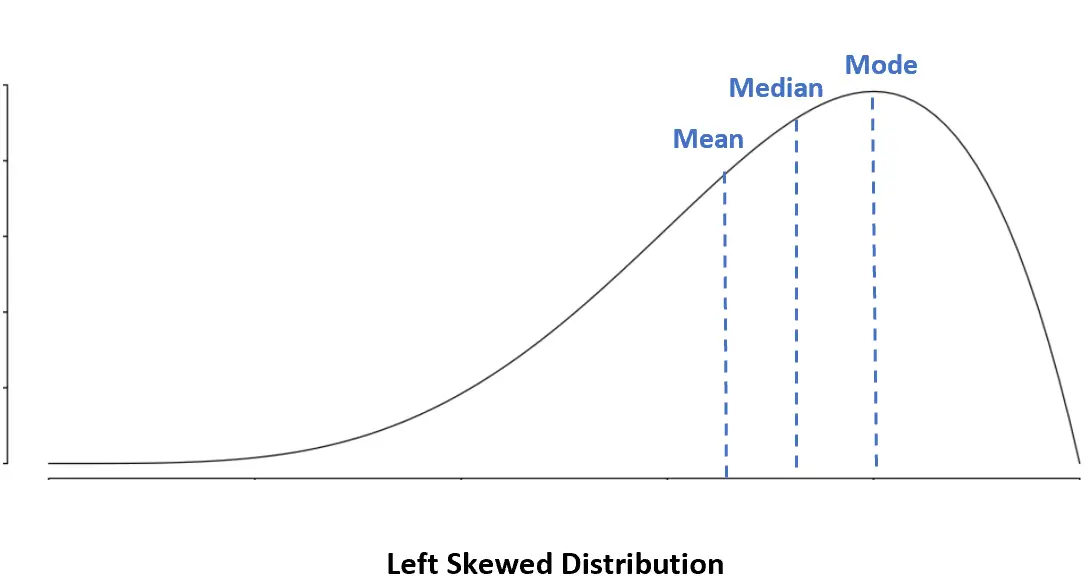
ဘယ်ဘက်စောင်းစောင်း ဖြန့်ဝေမှုတွင်၊ ပျမ်းမျှသည် ပျမ်းမျှထက် နည်းပါသည်။
ညာလှည့်ဖြန့်ချီခြင်း- မုဒ် < Median < ဆိုလိုရင်း
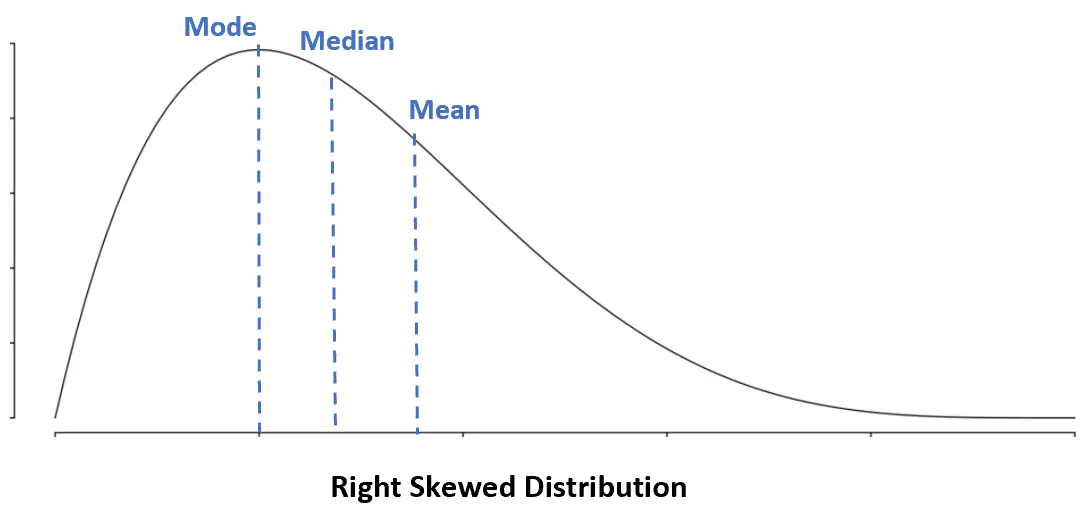
ညာဖက်လှည့်၍ ဖြန့်ဝေမှုတွင် ပျမ်းမျှသည် ပျမ်းမျှထက် ကြီးသည်။
ဘက်လိုက်မှုမရှိပါ- အဓိပ္ပါယ် = မီဒီယံ = မုဒ်

အချိုးညီသော ဖြန့်ဝေမှုတွင်၊ ပျမ်းမျှ၊ အလယ်အလတ်နှင့် မုဒ်တို့သည် တူညီကြသည်။
ထပ်လောင်းအရင်းအမြစ်များ
ဘယ် သို့မဟုတ် ညာ လှည့်၍ ဖြန့်သည်။
အချိုးညီသော ဖြန့်ဝေမှုများ- အဓိပ္ပါယ် + ဥပမာများ