Weibull ဖြန့်ချီရေး
ဤဆောင်းပါးတွင် Weibull ဖြန့်ဖြူးမှုသည် အဘယ်အရာနှင့် ၎င်းကိုအသုံးပြုကြောင်း ရှင်းပြထားသည်။ ထို့အပြင်၊ Weibull ဖြန့်ဖြူးမှု၏ ဂရပ်ဖစ်ကိုယ်စားပြုမှုနှင့် ဤဖြစ်နိုင်ခြေဖြန့်ဖြူးမှုအမျိုးအစား၏ ဂုဏ်သတ္တိများကား အဘယ်နည်း။
Weibull ဖြန့်ဖြူးမှုကား အဘယ်နည်း။
Weibull ဖြန့်ဖြူးမှုသည် အသွင်သဏ္ဌာန် ကန့်သတ်ဘောင် α နှင့် အတိုင်းအတာ ကန့်သတ်ချက် λ တို့ဖြင့် သတ်မှတ်ထားသော စဉ်ဆက်မပြတ် ဖြစ်နိုင်ခြေ ဖြန့်ဖြူးမှုတစ်ခုဖြစ်သည်။
စာရင်းဇယားများတွင်၊ Weibull ဖြန့်ဖြူးမှုကို ရှင်သန်မှုခွဲခြမ်းစိတ်ဖြာရန်အတွက် အဓိကအားဖြင့် အသုံးပြုပါသည်။ အလားတူ၊ Weibull ဖြန့်ဖြူးမှုတွင် မတူညီသောနယ်ပယ်များတွင် အသုံးချပရိုဂရမ်များစွာရှိသည်။ Weibull ဖြန့်ဖြူးမှုကို အသုံးပြုခြင်းအကြောင်း အသေးစိတ်ကို အောက်တွင် ဖော်ပြပါမည်။
![]()
စာရေးဆရာများအဆိုအရ Weibull ဖြန့်ဖြူးမှုကိုလည်း parameter သုံးခုဖြင့်ကန့်သတ်နိုင်သည်။ ထို့နောက်၊ threshold value ဟုခေါ်သော တတိယပါရာမီတာကို ပေါင်းထည့်သည်၊ ၎င်းသည် ဖြန့်ဖြူးမှုဂရပ်စတင်သည့် abscissa ကိုညွှန်ပြသည်။
Weibull ဖြန့်ဖြူးမှုကို 1951 ခုနှစ်တွင် အသေးစိတ်ဖော်ပြခဲ့သော ဆွီဒင် Waloddi Weibull ကို အမည်ပေးထားသည်။ သို့သော် Weibull ဖြန့်ဖြူးမှုကို 1927 ခုနှစ်တွင် Maurice Fréchet မှရှာဖွေတွေ့ရှိခဲ့ပြီး Rosin နှင့် Rammler မှ 1933 ခုနှစ်တွင် ပထမဆုံးအသုံးပြုခဲ့သည်။
Weibull ဖြန့်ချီရေး အစီအစဉ်ဆွဲခြင်း။
Weibull ဖြန့်ဖြူးမှု၏ အဓိပ္ပါယ်ဖွင့်ဆိုချက်ကို ကျွန်ုပ်တို့မြင်ပြီးသည်နှင့်၊ ၎င်း၏ ကန့်သတ်ချက်များ၏ တန်ဖိုးများပေါ်မူတည်၍ ၎င်း၏ ဂရပ်ဖစ်ကိုယ်စားပြုပုံ ကွဲပြားသည်ကို ကျွန်ုပ်တို့ မြင်တွေ့ရမည်ဖြစ်သည်။
အောက်တွင် Weibull ဖြန့်ဖြူးမှု၏ သိပ်သည်းဆလုပ်ဆောင်ပုံဂရပ်သည် ပုံသဏ္ဍာန်သတ်မှတ်ချက်နှင့် စကေးပါရာမီတာ၏တန်ဖိုးပေါ်မူတည်၍ ကွဲပြားပုံကို အောက်တွင် သင်ကြည့်ရှုနိုင်ပါသည်။
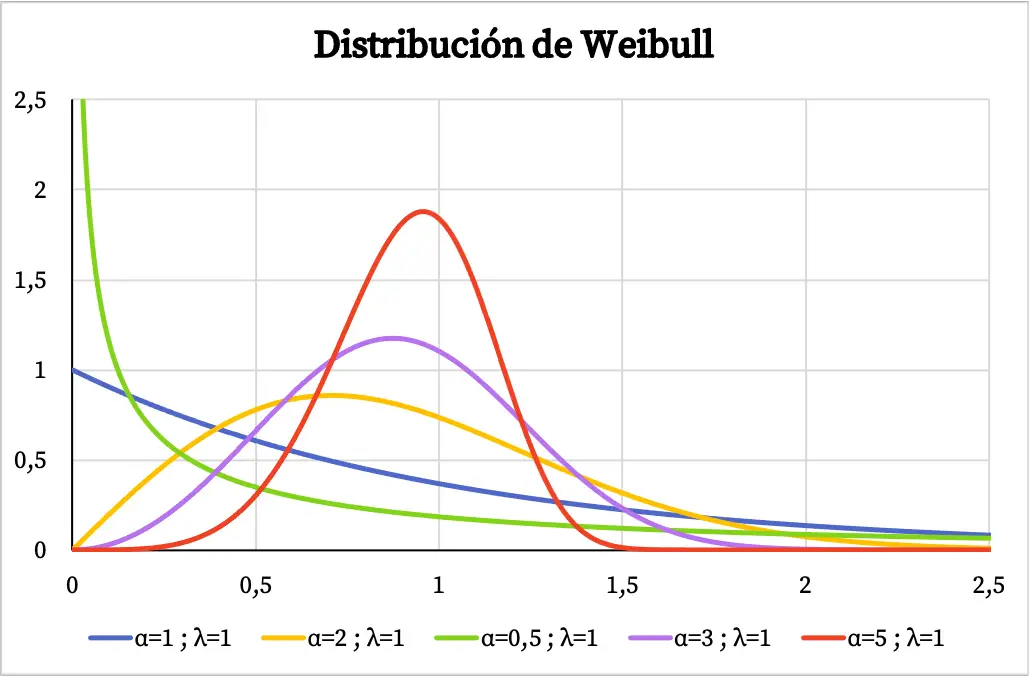
Weibull ဖြန့်ဝေမှုကို အချိန်၏လုပ်ဆောင်ချက်အဖြစ် စနစ်တစ်ခု၏ ကျရှုံးမှုနှုန်းကို စံနမူနာပြုရန်အတွက် အသုံးပြုသောအခါ ပုံသဏ္ဍာန်ဘောင် α ၏တန်ဖိုးသည် အောက်ပါတို့ကို ဆိုလိုသည်-
- α<1- အချိန်ကြာလာသည်နှင့်အမျှ ကျရှုံးမှုနှုန်း လျော့ကျသွားသည်။
- α=1- ကျရှုံးမှုနှုန်းသည် အချိန်နှင့်အမျှ ကိန်းသေနေပါသည်။
- α>1- ကျရှုံးမှုနှုန်းသည် အချိန်နှင့်အမျှ တိုးလာသည်။
အခြားတစ်ဖက်တွင်၊ အောက်ပါဂရပ်တွင် Weibull ဖြန့်ချီမှု၏ စုစည်းဖြစ်နိုင်ခြေလုပ်ဆောင်ချက်ကို ၎င်း၏ဝိသေသတန်ဖိုးများပေါ်တွင်အခြေခံ၍ ရေးဆွဲထားသည်ကို တွေ့နိုင်ပါသည်။
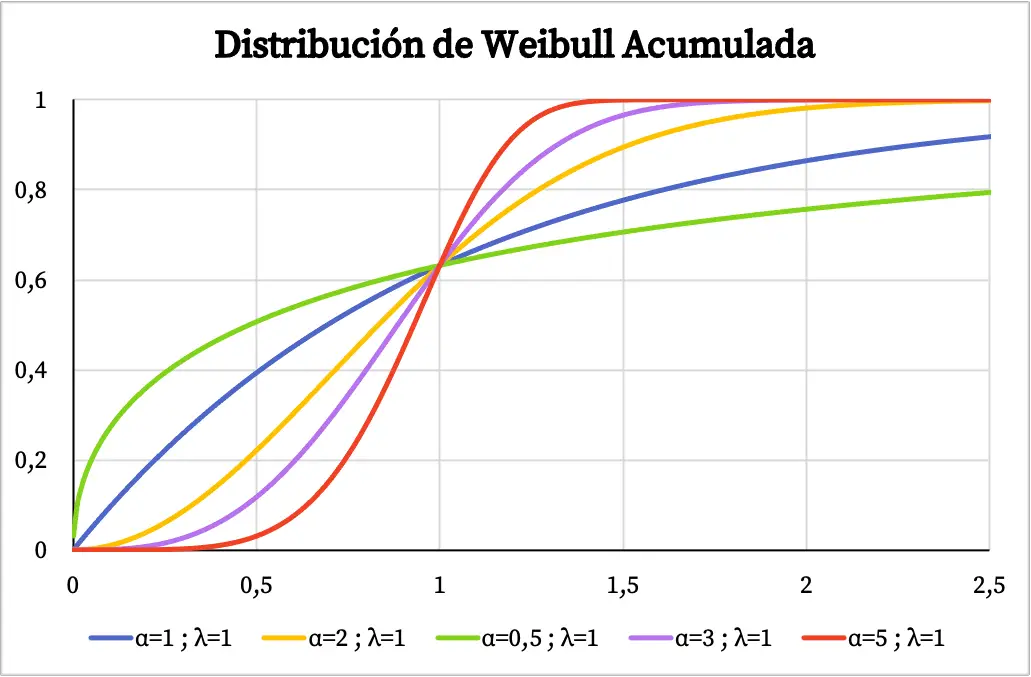
Weibull ဖြန့်ဖြူးခြင်း၏လက္ခဏာများ
Weibull ဖြန့်ဖြူးမှုတွင် အောက်ပါလက္ခဏာများ ရှိသည်။
- Weibull ဖြန့်ဝေမှုတွင် ၎င်း၏ဂရပ်ကို သတ်မှတ်သည့် လက္ခဏာရပ်နှစ်ခု ရှိသည်- ပုံသဏ္ဍာန်ဘောင် α နှင့် စကေးပါရာမီတာ λ။ ကန့်သတ်ချက်နှစ်ခုစလုံးသည် အပေါင်းကိန်းအစစ်အမှန်များဖြစ်သည်။
![\begin{array}{c}\alpha >0\\[2ex]\lambda >0\\[2ex]\text{Weibull}(\alpha,\lambda)\end{array}” title=” Rendered by QuickLaTeX.com” height=” 92″ width=” 101″ style=” vertical-align: 0px;” ></p>
</p>
<ul>
<li> Weibull ဖြန့်ဖြူးမှုသည် အပြုသဘောဆောင်သော abscissa တန်ဖိုးများကိုသာ လက်ခံသည်။</li>
</ul>
<p class=](https://statorials.org/wp-content/ql-cache/quicklatex.com-c8794febbd607514546841a325490654_l3.png)
![]()
- Weibull ဖြန့်ဖြူးမှု၏ပျမ်းမျှအား အောက်ပါဖော်မြူလာဖြင့် တွက်ချက်သည်-
![]()
- အခြားတစ်ဖက်တွင်၊ Weibull ဖြန့်ဖြူးမှု၏ကွဲပြားမှုကိုရှာဖွေရန် ဖော်မြူလာမှာ-
![]()
- α>1 ဖြင့် Weibull ဖြန့်ဝေမှုနောက်ဆက်တွဲဖြစ်သော ကျပန်းပြောင်းလဲနိုင်သောမုဒ်ကို အောက်ပါစကားရပ်ဖြင့် ဆုံးဖြတ်နိုင်သည်-
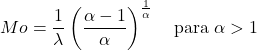
![]()
- အလားတူပင်၊ Weibull ဖြန့်ဖြူးမှု၏ တိုးပွားလာနိုင်သည့် ဖြစ်နိုင်ခြေလုပ်ဆောင်ချက်အတွက် ဖော်မြူလာမှာ-
![]()
- Weibull ဖြန့်ဖြူးမှု၏ အချိုးမညီသောကိန်းဂဏန်းအား အောက်ပါဖော်မြူလာကို အသုံးပြုခြင်းဖြင့် တွက်ချက်သည်-
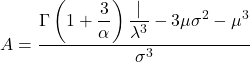
- နောက်ဆုံးတွင်၊ Weibull ဖြန့်ဖြူးမှု၏ kurtosis coefficient ကိုဆုံးဖြတ်ရန်ဖြစ်နိုင်စေသည့်ဖော်မြူလာမှာ အောက်ပါအတိုင်းဖြစ်သည်။
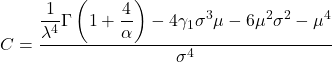
ရွှေ
![]()
Weibull ဖြန့်ဖြူးမှုဆိုင်ရာ အသုံးချမှုများ
Weibull ဖြန့်ချီရေးတွင်၊ အက်ပ်များစွာ ပါဝင်သည်-
- အသုံးချစာရင်းဇယားများတွင် Weibull ဖြန့်ဖြူးမှုကို ရှင်သန်မှုခွဲခြမ်းစိတ်ဖြာမှုတွင် အသုံးပြုသည်။
- အင်ဂျင်နီယာတွင်၊ Weibull ဖြန့်ဖြူးမှုကို ထုတ်လုပ်မှုအချိန်နှင့်သက်ဆိုင်သည့် လုပ်ဆောင်ချက်များကို နမူနာယူရန် အသုံးပြုသည်။
- ရေဒါစနစ်များတွင်၊ လက်ခံရရှိသောအချက်ပြမှု၏ပျံ့နှံ့မှုကိုပုံတူအောင်လုပ်ပါ။
- အာမခံကဏ္ဍတွင် တောင်းဆိုမှုအတိုင်းအတာကို စံနမူနာပြုရန်။
- ဥပမာအားဖြင့်၊ မိုးလေဝသပညာတွင် မတူညီသော လေတိုက်နှုန်းများ၏ ကြိမ်နှုန်းကို စံနမူနာပြုရန်။