R တွင် wilcoxon ရေးထိုးထားသောအဆင့်စစ်ဆေးမှုကိုမည်သို့လုပ်ဆောင်ရမည်နည်း။

Wilcoxon Signed-Rank test သည် တွဲထားသော t test ၏ nonparametric ဗားရှင်းဖြစ်သည် ။ နမူနာနှစ်ခုကြား ကွဲပြားမှုကို ပုံမှန်ဟု မယူဆနိုင်သောအခါ လူဦးရေနှစ်ခု၏ နည်းလမ်းများကြား သိသာထင်ရှားသော ခြားနားမှု ရှိ၊ မရှိ စမ်းသပ်ရန် ၎င်းကို အသုံးပြုသည်။

ဤသင်ခန်းစာသည် R တွင် Wilcoxon လက်မှတ်ရေးထိုးထားသော အဆင့်စစ်ဆေးမှုကို မည်သို့လုပ်ဆောင်ရမည်ကို ရှင်းပြထားသည်။

ဥပမာ- Wilcoxon သည် R တွင် အဆင့်စစ်ဆေးမှုကို လက်မှတ်ရေးထိုးခဲ့သည်။

ဘတ်စကတ်ဘောနည်းပြတစ်ဦးသည် အချို့သောလေ့ကျင့်ရေးအစီအစဉ်တစ်ခုသည် ၎င်း၏ကစားသမားများပြုလုပ်သော အခမဲ့ပစ်လွှတ်မှုအရေအတွက်ကို တိုးပေးမည်ဆိုပါက သိလိုသည်ဆိုပါစို့။ ၎င်းကို စမ်းသပ်ရန်အတွက် ကစားသမား ၁၅ ဦးအား လေ့ကျင့်ရေးအစီအစဉ်မစမီနှင့် အပြီးတွင် တစ်ကြိမ်လျှင် အကြိမ် ၂၀ အခမဲ့ လွှင့်ပစ်ရန် တောင်းဆိုခဲ့သည်။

ကစားသမားတစ်ဦးစီကို သူ့ကိုယ်သူ တွဲနိုင်သောကြောင့်၊ နည်းပြသည် လေ့ကျင့်ရေးအစီအစဉ်မတိုင်မီနှင့် အပြီးတွင် ပြုလုပ်သော ပျမ်းမျှအခမဲ့ပစ်လွှတ်မှုအရေအတွက်ကြား သိသာထင်ရှားသော ကွာခြားမှုရှိမရှိ ဆုံးဖြတ်ရန် တွဲထားသည့် t-test ကို အသုံးပြုရန် စီစဉ်ခဲ့သည်။ လေ့ကျင့်ရေး။ သို့သော်၊ ကွဲပြားမှုများကို ဖြန့်ဝေခြင်းသည် ပုံမှန်မဟုတ်သောကြောင့် လေ့ကျင့်သူသည် Wilcoxon Signed-Rank စာမေးပွဲကို အစားထိုးအသုံးပြုသည်။

အောက်ပါဇယားတွင် ကစားသမား ၁၅ ဦးစီမှ လေ့ကျင့်ရေးအစီအစဉ်မစမီနှင့် အပြီးတွင် (အကြိမ် ၂၀ တွင်) အခမဲ့ပစ်လွှတ်မှုအရေအတွက်ကို ဖော်ပြသည်-

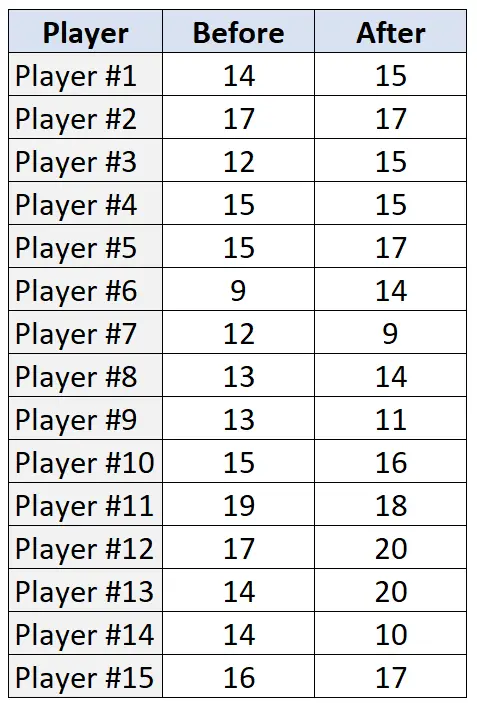
ဤဒေတာတွင် R ရှိ Wilcoxon Signed-Rank Test ကိုလုပ်ဆောင်ရန်၊ အောက်ပါ syntax ကိုအသုံးပြုသည့် wilcox.test() လုပ်ဆောင်ချက်ကို ကျွန်ုပ်တို့အသုံးပြုနိုင်သည်-

wilcox.test(x၊ y၊ even = TRUE)

ရွှေ-

• x၊ y- ဒေတာတန်ဖိုးများ၏ vector နှစ်ခု
• တွဲထားသည်- ၎င်းကို TRUE ဟုသတ်မှတ်ခြင်းသည် ကျွန်ုပ်တို့၏ vector နှစ်ခုတွင် တွဲထားသောဒေတာပါရှိသည်ကို R ကိုပြောပြသည်။

ဤဒေတာအတွက် Wilcoxon Signed-Rank စမ်းသပ်မှုကို လုပ်ဆောင်ရန် ဤလုပ်ဆောင်ချက်ကို အသုံးပြုနည်းကို အောက်ပါကုဒ်က သရုပ်ပြသည်-

 #create the two vectors of data
before <- c(14, 17, 12, 15, 15, 9, 12, 13, 13, 15, 19, 17, 14, 14, 16)
after <- c(15, 17, 15, 15, 17, 14, 9, 14, 11, 16, 18, 20, 20, 10, 17)

#perform Wilcoxon Signed-Rank Test
wilcox.test(before, after, paired=TRUE)

	Wilcoxon signed rank test with continuity correction

data: before and after
V = 29.5, p-value = 0.275
alternative hypothesis: true location shift is not equal to 0

စမ်းသပ်မှုစာရင်းအင်းသည် 29.5 ဖြစ်ပြီး သက်ဆိုင်ရာ p-value သည် 0.275 ဖြစ်သည်။ ဤ p-value သည် 0.05 ထက်မနည်းသောကြောင့်၊ null hypothesis ကို ငြင်းပယ်ရန် ပျက်ကွက်ပါသည်။ ကစားသမားများ လေ့ကျင့်ရေးအစီအစဉ်တွင် ပါဝင်ခြင်းမပြုမီနှင့် အပြီးတွင် အလွတ်ပစ်ခြင်းအရေအတွက်တွင် ကိန်းဂဏန်းအရ သိသာထင်ရှားသော ကွာခြားချက်မရှိပါ။

ပုံသေအားဖြင့်၊ ဤလုပ်ဆောင်ချက်သည် တစ်ဖက်သတ် Wilcoxon Signed-Rank စမ်းသပ်မှုကို လုပ်ဆောင်သည်၊ သို့သော် အခြား အငြင်းအခုံကို အသုံးပြု၍ ဘယ်သန်စမ်းသပ်မှု သို့မဟုတ် ညာသန်စမ်းသပ်မှုကို သင်သတ်မှတ်နိုင်သည်-

 #perform left-tailed Wilcoxon Signed-Rank Test
wilcox.test(before, after, paired=TRUE, alternative="less")

	Wilcoxon signed rank test with continuity correction

data: before and after
V = 29.5, p-value = 0.1375
alternative hypothesis: true location shift is less than 0

#perform right-tailed Wilcoxon Signed-Rank Test
wilcox.test(before, after, paired=TRUE, alternative="greater")

	Wilcoxon signed rank test with continuity correction

data: before and after
V = 29.5, p-value = 0.8774
alternative hypothesis: true location shift is greater than 0

ထပ်လောင်းအရင်းအမြစ်များ

Wilcoxon Signed Rank Test အတွက် နိဒါန်း
Wilcoxon Signed Place Test Calculator