Yate continuity correction- အဓိပ္ပါယ်နှင့် ဥပမာ

သီးခြားကိန်းရှင်နှစ်ခုကြားတွင် သိသာထင်ရှားသော ဆက်စပ်မှု ရှိ၊ မရှိ ဆုံးဖြတ်ရန် လွတ်လပ်ရေး ချီစတုရန်းစစ်ဆေးမှု ကို အသုံးပြုသည်။

ဤစစ်ဆေးမှုသည် အောက်ပါ null နှင့် အခြားအခြားသော အယူအဆများကို အသုံးပြုသည်-

• H ₀ : (null hypothesis) ကိန်းရှင်နှစ်ခုသည် သီးခြားဖြစ်သည်။
• H ₁ : (အစားထိုးယူဆချက်) ကိန်းရှင်နှစ်ခုသည် သီးခြား မဟုတ်ပေ ။ (ဆိုလိုသည်မှာ ၎င်းတို့သည် ဆက်စပ်နေသည်)

ဤစစ်ဆေးမှုအတွက် Chi-square x ² စမ်းသပ်မှုစာရင်းအင်းကို တွက်ချက်ရန် အောက်ပါဖော်မြူလာကို အသုံးပြုပါသည်။

X ² = Σ(O _i -E _i ) ² / E _i

ရွှေ-

• Σ- သည် “ ပေါင်း” ဟု အဓိပ္ပါယ်ရသော ဖန်စီသင်္ကေတတစ်ခုဖြစ်သည်။
• O: သတိပြုမိသည်။
• E: မျှော်မှန်းတန်ဖိုး

ဤစမ်းသပ်မှုသည် စဉ်ဆက်မပြတ် ဖြန့်ဖြူးမှုဖြစ်သည့် Chi-square ဖြန့်ဖြူးမှုဖြင့် အနီးစပ်ဆုံး ဖြစ်နိုင်ခြေရှိသော ကြိမ်နှုန်းများ၏ သီးခြားဖြစ်နိုင်ချေများကို ခန့်မှန်းနိုင်သည်ဟု ယူဆသည်။

သို့သော်၊ ဤယူဆချက်သည် အနည်းငယ် မှားယွင်းနေလေ့ရှိပြီး ရလဒ်စမ်းသပ်မှုစာရင်းဇယားသည် အထက်ဘက်သို့ ဘက်လိုက်နေတတ်သည်။

ဤဘက်လိုက်မှုအတွက် ပြုပြင်ရန်၊ ကျွန်ုပ်တို့သည် ဖော်မြူလာ ^X2 တွင် အောက်ပါတည်းဖြတ်ချက်ကို ကျင့်သုံးသည့် Yate ၏ အဆက်မပြတ် တည့်မတ်မှုကို အသုံးပြုနိုင်သည် ။

X ² = Σ(|O _i -E _i |– 0.5) ² / E _i

ယေဘူယျအားဖြင့် ကျွန်ုပ်တို့သည် အရေးပေါ်အခြေအနေဇယားရှိ အနည်းဆုံးဆဲလ်တစ်ခုတွင် မျှော်လင့်ထားသည့်အကြိမ်ရေ 5 ထက်နည်းသောအချိန်တွင်သာ ဤပြင်ဆင်ချက်ကို ကျွန်ုပ်တို့အသုံးပြုပါသည်။

ဥပမာ- Yate ၏ အဆက်မပြတ် တည့်မတ်မှု လျှောက်လွှာ

နိုင်ငံရေး ပါတီတစ်ခုအတွက် ဦးစားပေးမှုတွင် ကျား၊မ ဆက်စပ်မှု ရှိ၊ မရှိ သိလိုသည်ဆိုပါစို့။ ကျွန်ုပ်တို့သည် မဲဆန္ဒရှင် ၄၀ ဦး၏ ရိုးရှင်းသော ကျပန်းနမူနာကို ယူကာ ၎င်းတို့၏ နိုင်ငံရေး ပါတီကို နှစ်သက်မှုအကြောင်း မေးမြန်းပါသည်။ အောက်ပါဇယားသည် စစ်တမ်း၏ရလဒ်များကို ဖော်ပြသည်။

Yate ၏ အဆက်မပြတ် တည့်မတ်မှုဖြင့် လွတ်လပ်ရေး chi-square စမ်းသပ်မှု ပြုလုပ်နည်းမှာ အောက်ပါအတိုင်းဖြစ်သည် ။

စောင့်ကြည့်ထားသော တန်ဖိုးများ-

မျှော်မှန်းတန်ဖိုးများ-

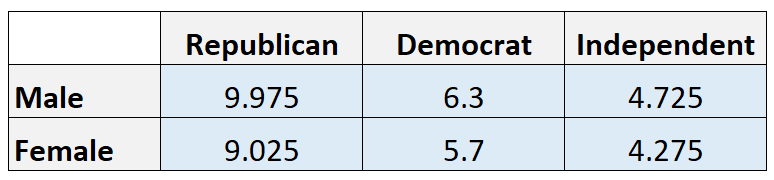
မှတ်ချက်။ ဥပမာအားဖြင့်၊ မျှော်မှန်းထားသော ရီပတ်ဘလစ်ကန် အမျိုးသား အရေအတွက်မှာ (21*19)/40 = 9.975 ဖြစ်သည်။

^{Chi –} _{စတုရန်း စမ်းသပ် စာရင်းအင်း} _

• (|8-9.975| – 0.5) ² / 9.975 = 0.218
• (|9-6.3| – 0.5) ² /6.3 = 0.768
• (|4-4.725| – 0.5) ² /4.725 = 0.011
• (|11-9.025| – 0.5) ² / 9.025 = 0.241
• (|3-5.7| – 0.5) ² /5.7 = 0.849
• (|5-4.275|– 0.5) ² /4.275 = 0.012

^{ဒီတော့} ၊

P-value- P-value ဂဏန်းတွက်စက်မှ chi-square အရ ၊ လွတ်လပ်မှု 2 ဒီဂရီရှိသော chi-square စမ်းသပ်မှုကိန်းဂဏန်းနှင့် သက်ဆိုင်သည့် p-တန်ဖိုးသည် 0.3501 ဖြစ်သည်။

ဤ p-value သည် 0.05 ထက်မနည်းသောကြောင့်၊ null hypothesis ကို ငြင်းပယ်မည်မဟုတ်ပါ။ ဆိုလိုသည်မှာ ကျား၊မ နှင့် နိုင်ငံရေး ပါတီများ၏ နှစ်သက်ရာများကြားတွင် ဆက်စပ်မှုရှိသည်ဟု ဆိုရန် လုံလောက်သော အထောက်အထား မရှိပါ။