မတူညီသောဖြန့်ဝေမှုများ၏ z ရမှတ်များကို နှိုင်းယှဉ်ခြင်း။

z-score သည် တစ်ဦးချင်းဒေတာတန်ဖိုးသည် ပျမ်းမျှအားဖြင့် စံသွေဖည်မည်မျှရှိသည်ကို ပြောပြသည်။ အောက်ပါအတိုင်း တွက်ချက်သည်။

z-score = (x – μ) / σ

ရွှေ-

• x- တစ်ဦးချင်းဒေတာတန်ဖိုး
• μ: လူဦးရေ ပျမ်းမျှ
• σ: လူဦးရေစံသွေဖည်

တစ်ဦးချင်းတန်ဖိုးအတွက် z-score ကို အောက်ပါအတိုင်း အဓိပ္ပာယ်ဖွင့်ဆိုနိုင်သည်-

• အပြုသဘော z-ရမှတ်- တစ်ဦးချင်းတန်ဖိုးသည် ပျမ်းမျှအထက်ဖြစ်သည်။
• အနုတ်လက္ခဏာ z-ရမှတ်- တစ်ဦးချင်းတန်ဖိုးသည် ပျမ်းမျှထက် နိမ့်သည်။
• z-ရမှတ် 0- တစ်ဦးချင်းတန်ဖိုးသည် ပျမ်းမျှနှင့် ညီမျှသည်။

မတူညီသော ဖြန့်ဝေမှုနှစ်ခုမှ ဒေတာအချက်နှစ်ခု၏ ဆွေမျိုးအနေအထားကို နှိုင်းယှဉ်လိုသောအခါ Z ရမှတ်များသည် အထူးအသုံးဝင်ပါသည်။ ယင်းကို သရုပ်ဖော်ရန် အောက်ပါဥပမာကို သုံးသပ်ကြည့်ပါ။

ဥပမာ- Z ရမှတ်များကို နှိုင်းယှဉ်ခြင်း။

ကောလိပ်စာမေးပွဲတစ်ခုတွင် ရမှတ်များကို ပုံမှန်အားဖြင့် ပျမ်းမျှ μ = 80 နှင့် စံသွေဖည်မှု σ = 4 ဖြင့် ဖြန့်ဝေထားသည်။ Duane သည် ဤစာမေးပွဲတွင် 84 ရမှတ်ဖြစ်သည်။

အခြားကောလိပ်စာမေးပွဲတွင် ရမှတ်များကို ပုံမှန်အားဖြင့် ပျမ်းမျှ μ = 85 နှင့် စံသွေဖည်မှု σ = 8 ဖြင့် ဖြန့်ဝေပါသည်။ ဒက်ဘီသည် ထိုစာမေးပွဲတွင် 90 ရရှိသည်။

စာမေးပွဲရမှတ်များကို ၎င်းတို့၏ကိုယ်ပိုင်ဖြန့်ဝေမှုနှင့် နှိုင်းယှဉ်ပါက ၎င်းတို့၏ စာမေးပွဲတွင် အကောင်းဆုံးရလဒ်များကို မည်သူရရှိခဲ့သနည်း။

ဤမေးခွန်းကိုဖြေဆိုရန်၊ လူတစ်ဦးစီ၏ စာမေးပွဲရမှတ်၏ z-score ကို တွက်ချက်နိုင်သည်-

Duane ၏ z ရမှတ် = (x – μ) / σ = (84 – 80) / 4 = 4 / 4 = 1

ဒက်ဘီ၏ z-ရမှတ် = (x – μ) / σ = (90 – 85) / 8 = 5/8 = 0.625

ဒက်ဘီသည် ရမှတ်ပိုမြင့်သော်လည်း Duane ၏ရမှတ်သည် ၎င်း၏ သီးခြားစာမေးပွဲဖြေဆိုမှုနှင့် နှိုင်းယှဉ်ပါက အမှန်တကယ်မြင့်မားသည်။

ဒါကို နားလည်ဖို့က အခြေအနေကို မြင်ယောင်ဖို့ ကူညီပေးတယ်။ ဤတွင် Duane ၏ရမှတ်သည် ၎င်း၏ သီးခြား စာမေးပွဲ ကွဲလွဲချက်များနှင့် နှိုင်းယှဉ်ကြည့်ပါ ။

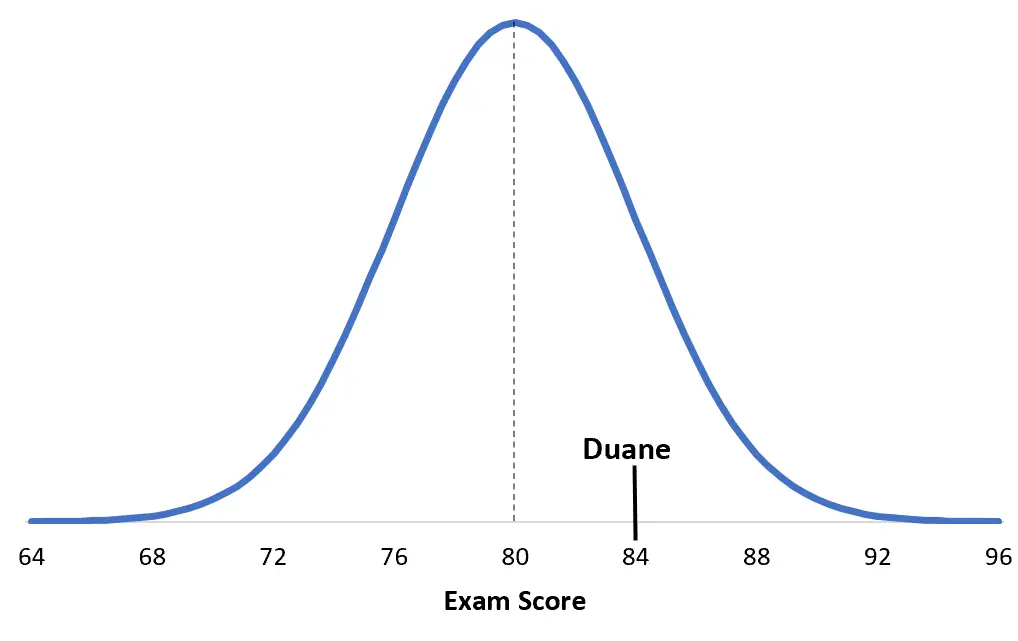
ပြီးတော့ ဒါက Debbie ရဲ့ စာမေးပွဲဖြေမှုကနေ ရမှတ်ပါ။

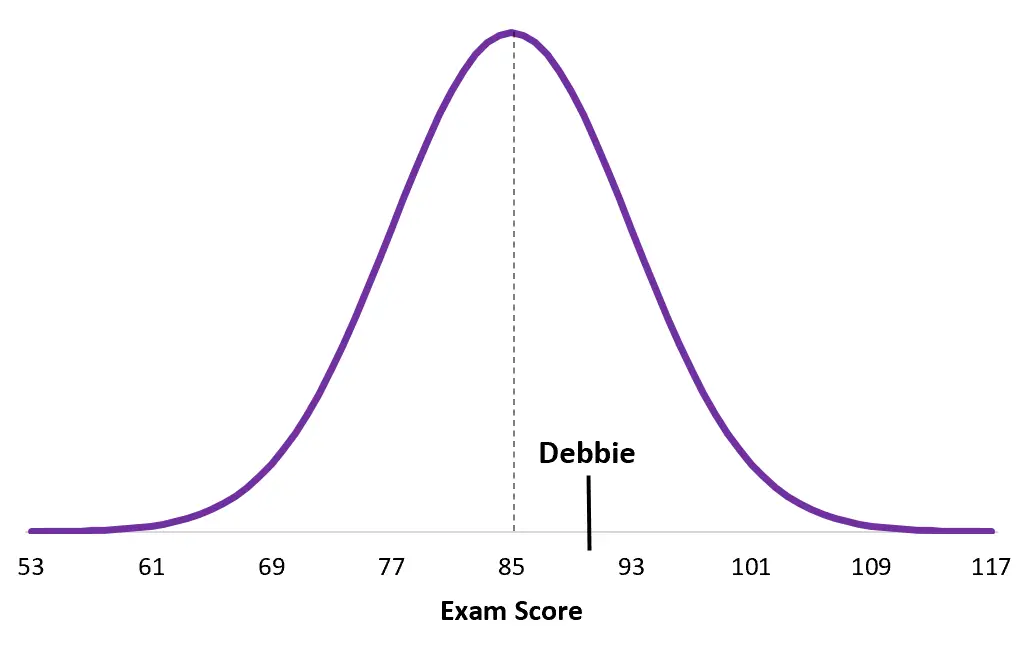
ဒက်ဘီ၏ရမှတ်သည် Duane ၏ပျမ်းမျှလူဦးရေထက် မည်မျှနီးကပ်သည်ကို သတိပြုပါ။ သူမသည် စုစုပေါင်းရမှတ် ပိုမြင့်သော်လည်း၊ သူမ၏ သီးခြားစာမေးပွဲတွင် ပျမ်းမျှရမှတ်က ပိုများသောကြောင့် သူမ၏ z-ရမှတ်သည် နိမ့်ပါသည်။

ဤဥပမာသည် မတူညီသောဖြန့်ဝေမှုများမှ ဒေတာတန်ဖိုးများကို နှိုင်းယှဉ်ရန်အတွက် အဘယ်ကြောင့် ဤမျှအသုံးဝင်ပုံကို ဥပမာပေးဖော်ပြသည်- z-scores သည် ဖြန့်ဝေမှုများ၏ ပျမ်းမျှနှင့် စံသွေဖည်မှုများကို ထည့်သွင်းစဉ်းစားသည်၊ ၎င်းသည် မတူညီသောဖြန့်ဝေမှုများမှ ဒေတာတန်ဖိုးများကို နှိုင်းယှဉ်ကာ မည်သည့်အရာဖြစ်သည်ကို သိနိုင်သည်။ ၎င်းတို့၏ကိုယ်ပိုင်ဖြန့်ဝေမှုများနှင့်နှိုင်းယှဉ်ပါကပိုမိုမြင့်မားသည်။

ထပ်လောင်းအရင်းအမြစ်များ

Z ရမှတ်ဂဏန်းတွက်စက်
Z ရမှတ်ဂဏန်းတွက်စက် နှိုင်းယှဉ်