Ti-84 ဂဏန်းတွက်စက်တွင် critical z တန်ဖိုးကို မည်သို့ရှာမည်နည်း။
သင်ယူဆချက်စမ်းသပ်မှုတစ်ခုလုပ်ဆောင်တိုင်း၊ သင်သည် စစ်ဆေးမှုစာရင်းအင်းတစ်ခုကို ရရှိမည်ဖြစ်သည်။ အဆိုပြုချက်စစ်ဆေးမှုရလဒ်များသည် ကိန်းဂဏန်းအချက်အလတ်များ သိသာမှုရှိမရှိ ဆုံးဖြတ်ရန်၊ စမ်းသပ်မှုစာရင်းအင်းအား အရေးကြီးသော Z တန်ဖိုး နှင့် နှိုင်းယှဉ်နိုင်သည်။ စမ်းသပ်စာရင်းအင်း၏ ပကတိတန်ဖိုးသည် အရေးကြီးသော Z တန်ဖိုးထက် ကြီးပါက၊ စစ်ဆေးမှုရလဒ်များသည် စာရင်းအင်းအရ သိသာထင်ရှားပါသည်။
TI-84 ဂဏန်းတွက်စက်ပေါ်တွင် အရေးကြီးသောတန်ဖိုး Z ကိုရှာဖွေရန်၊ အောက်ပါလုပ်ဆောင်ချက်ကို သင်အသုံးပြုနိုင်သည်-
invNorm(ဖြစ်နိုင်ခြေ၊ μ၊ σ)
ရွှေ-
- ဖြစ်နိုင်ခြေ- အရေးပါမှုအဆင့်
- μ: လူဦးရေ ပျမ်းမျှ
- σ: လူဦးရေစံသွေဖည်
2nd ကိုနှိပ်ပြီး vars ကိုနှိပ်ခြင်းဖြင့် ဤလုပ်ဆောင်ချက်ကို TI-84 ဂဏန်းတွက်စက်ပေါ်တွင် သင်ဝင်ရောက်နိုင်သည်။ ၎င်းသည် သင့်အား invNorm() ကို သုံးနိုင်သည့် DISTR ဖန်သားပြင်သို့ ခေါ်ဆောင်သွားပါမည်။

ဤသင်ခန်းစာသည် TI-84 ဂဏန်းတွက်စက်ပေါ်တွင် အရေးကြီးသော Z တန်ဖိုးများကို ရှာဖွေရန် invNorm() လုပ်ဆောင်ချက်ကို အသုံးပြုခြင်း၏ ဥပမာများစွာကို မျှဝေထားသည်။
ဥပမာ 1- ဘယ်ဘက်ရှိ စမ်းသပ်မှုအတွက် အရေးကြီးသောတန်ဖိုး Z
မေးခွန်း- သိသာထင်ရှားမှုအဆင့် 0.05 ရှိသော ဘယ်ဘက်စမ်းသပ်မှုအတွက် အရေးကြီးသော Z တန်ဖိုးကို ရှာပါ။
အဖြေ- invNorm.05, 0, 1) = -1.6449
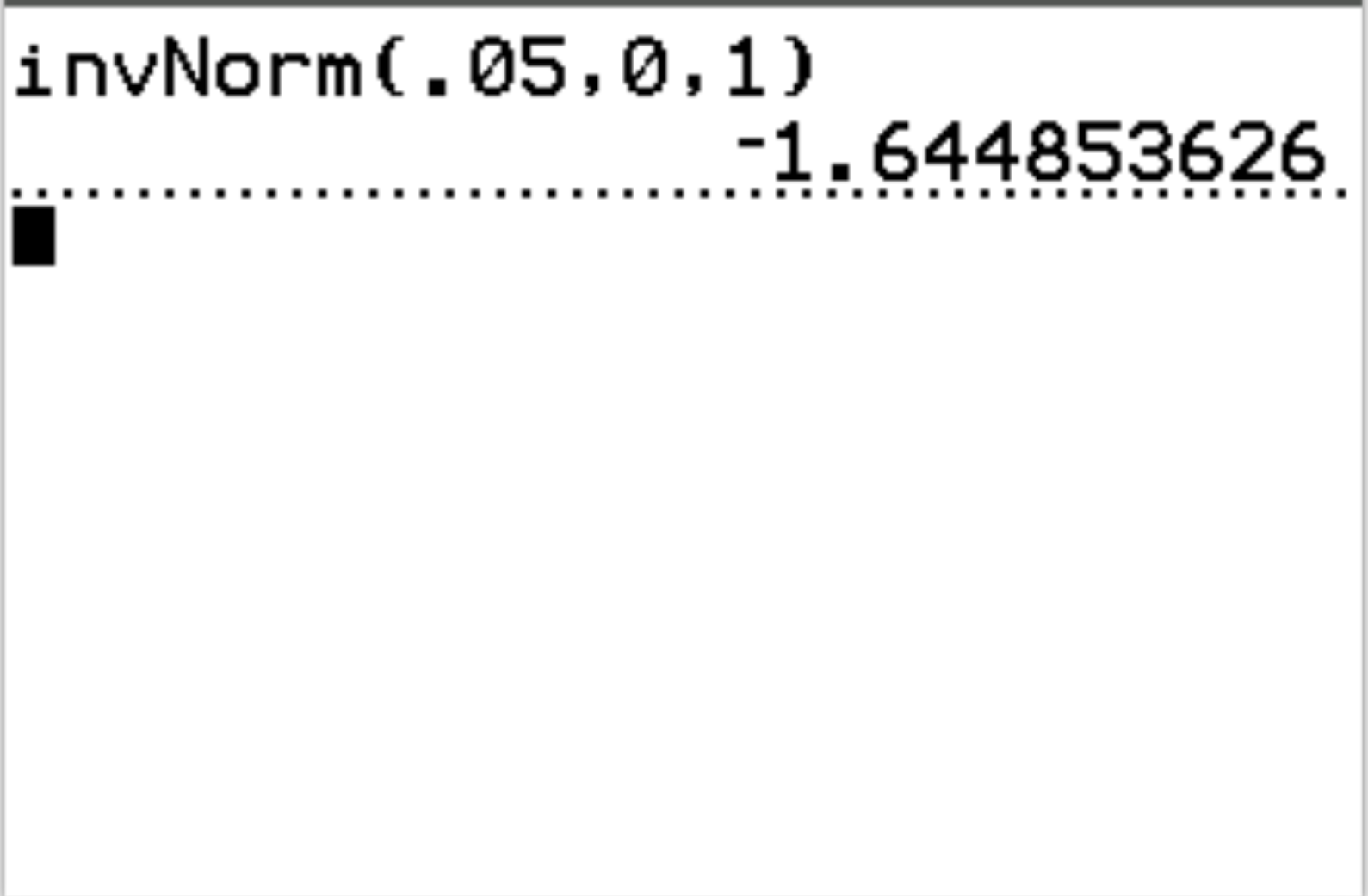
အဓိပ္ပာယ်ဖွင့်ဆိုချက်- စမ်းသပ်မှုစာရင်းအင်းသည် -1.6449 ထက်နည်းပါက စစ်ဆေးမှုရလဒ်များသည် α = 0.05 တွင် ကိန်းဂဏန်းအရ သိသာထင်ရှားပါသည်။
ဥပမာ 2- ဖြောင့်အမြီးစမ်းသပ်မှုအတွက် Critical Z တန်ဖိုး
မေးခွန်း- သိသာထင်ရှားမှုအဆင့် 0.10 ဖြင့် ညာဘက်နှစ်ခြမ်းစမ်းသပ်မှုအတွက် အရေးကြီးသော Z တန်ဖိုးကို ရှာပါ။
အဖြေ- invT(1-.10၊ 0၊ 1) = 1.2816
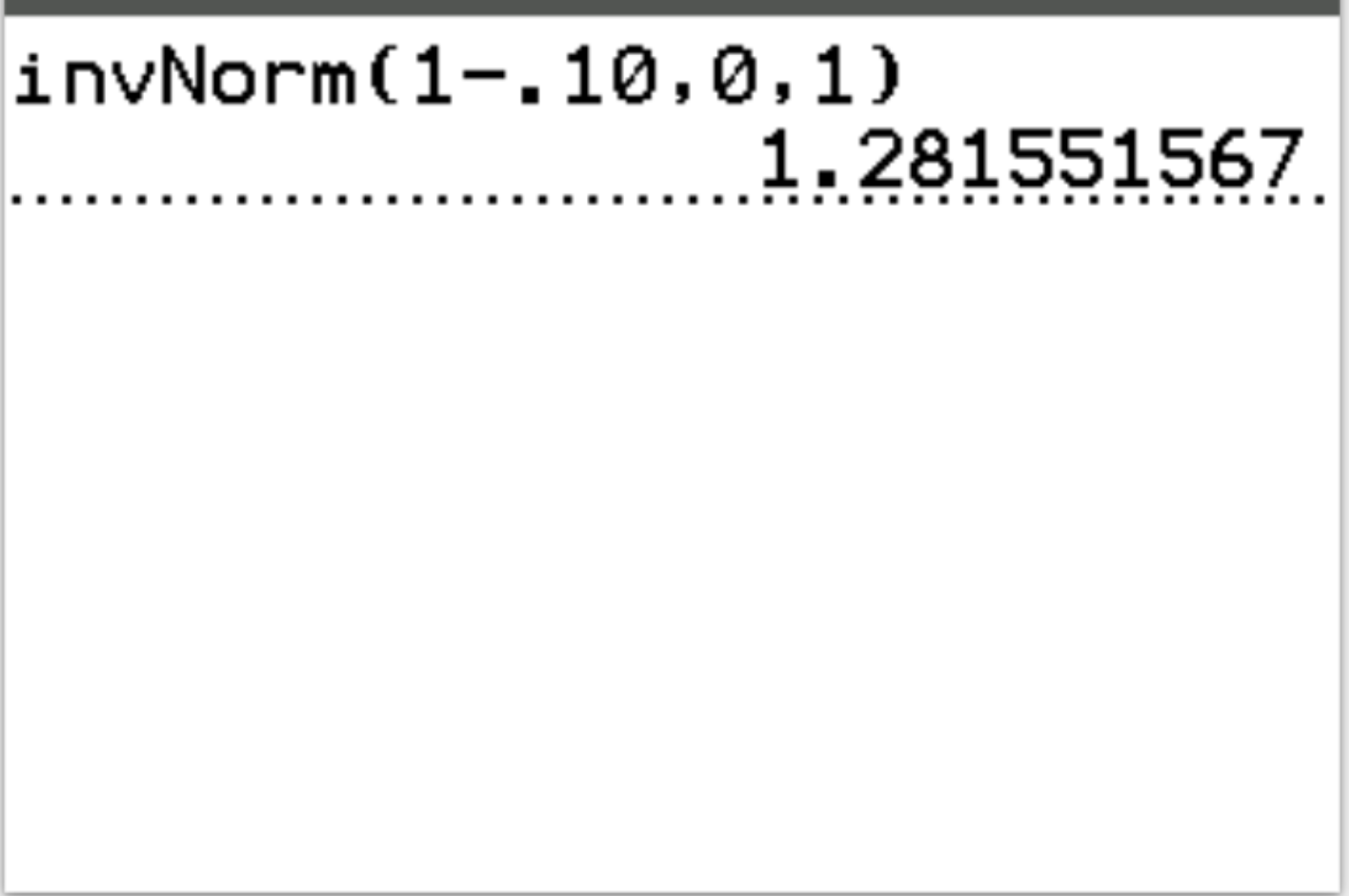
အဓိပ္ပာယ်ဖွင့်ဆိုချက်- စစ်ဆေးမှုစာရင်းအင်းသည် 1.2816 ထက် ကြီးပါက စစ်ဆေးမှုရလဒ်များသည် α = 0.10 တွင် ကိန်းဂဏန်းအရ သိသာထင်ရှားပါသည်။
ဥပမာ 3- နှစ်ဘက်စမ်းသပ်မှုအတွက် အရေးကြီးသော Z တန်ဖိုး
မေးခွန်း- သိသာထင်ရှားမှုအဆင့် 0.05 ဖြင့် အမြီးနှစ်ခုစမ်းသပ်မှုအတွက် အရေးကြီးသော Z တန်ဖိုးကို ရှာပါ။
အဖြေ- invNorm.05/2, 0, 1) = -1.96၊ 1.96
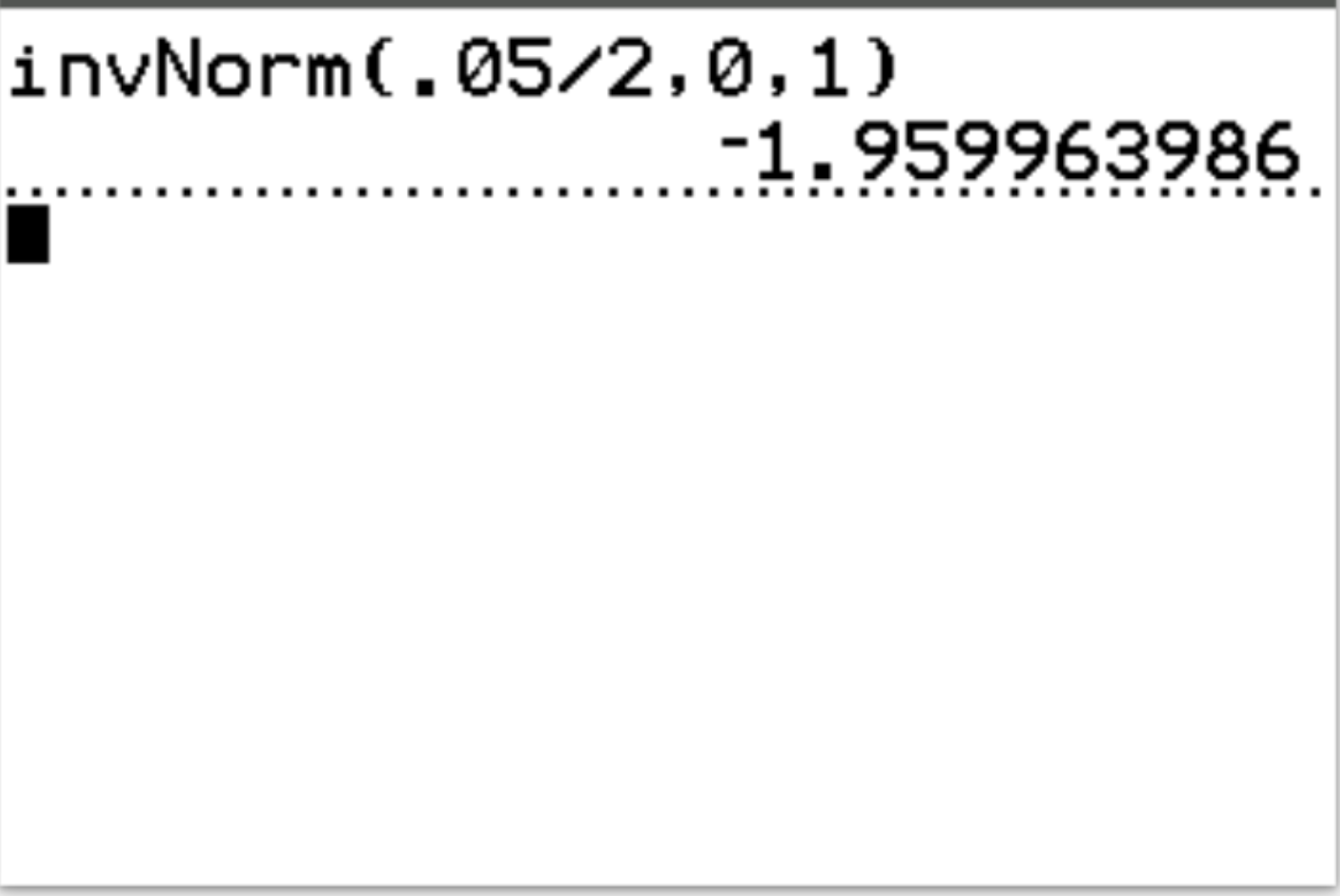
စကားပြန်- ဤအရာသည် အမြီးနှစ်ပိုင်းစမ်းသပ်မှုဖြစ်သောကြောင့်၊ ကျွန်ုပ်တို့တွင် အမှန်တကယ် အရေးကြီးသောတန်ဖိုးနှစ်ခုရှိသည် –1.96 နှင့် 1.96 ဖြစ်သည်။ စမ်းသပ်မှုစာရင်းအင်းသည် -1.96 ထက်နည်းပါက သို့မဟုတ် 1.96 ထက် ပိုများပါက၊ စစ်ဆေးမှုရလဒ်များသည် α = 0.05 တွင် ကိန်းဂဏန်းအရ သိသာထင်ရှားပါသည်။