Z table ကိုအသုံးပြုနည်း (ဥပမာများနှင့်အတူ)

a z table သည် စံပုံမှန် ဖြန့်ဖြူးမှုတစ်ခုတွင် တန်ဖိုးများ၏ ရာခိုင်နှုန်းအချို့ z ရမှတ်အောက် ကျဆင်းသွားသည်ကို ပြောပြသော ဇယားတစ်ခုဖြစ်သည်။

z-score သည် စံနှုန်းသွေဖည်မှု မည်မျှရှိသည်ကို သင့်အား ပျမ်းမျှအားဖြင့် ဒေတာတန်ဖိုးတစ်ခုစီမှ ကျဆင်းစေပါသည်။ အောက်ပါအတိုင်း တွက်ချက်သည်။

z-score = (x – μ) / σ

ရွှေ-

• x- တစ်ဦးချင်းဒေတာတန်ဖိုး
• μ: လူဦးရေ ပျမ်းမျှ
• σ: လူဦးရေစံသွေဖည်

ဤသင်ခန်းစာတွင် z ဇယားကိုအသုံးပြုခြင်း၏နမူနာများစွာကိုပြသထားသည်။

ဥပမာ ၁

အချို့သော ကောလိပ်ဝင်ခွင့်စာမေးပွဲတွင် ရမှတ်များကို ပုံမှန်အားဖြင့် ပျမ်းမျှ μ = 82 နှင့် စံသွေဖည်မှု σ = 8 ဖြင့် ခွဲဝေပေးပါသည်။ စာမေးပွဲတွင် ကျောင်းသားများ၏ ခန့်မှန်းခြေအားဖြင့် 84 အောက်တွင် ရမှတ်သည် အဘယ်ရာခိုင်နှုန်းနည်း။

အဆင့် 1- z-score ကိုရှာပါ။

ပထမဦးစွာ၊ စာမေးပွဲရမှတ် 84 နှင့်ဆက်စပ်သော z-score ကိုတွေ့ရပါမည်။

z-ရမှတ် = (x – μ) / σ = (84 – 82) / 8 = 2/8 = 0.25

အဆင့် 2- z ရမှတ်နှင့် ကိုက်ညီသော ရာခိုင်နှုန်းကို ရှာဖွေရန် z ဇယားကို အသုံးပြုပါ။

ထို့နောက် z ဇယားရှိ တန်ဖိုး 0.25 ကို ရှာဖွေပါမည်။

ကျောင်းသားများ၏ 59.87% ခန့်သည် ဤစာမေးပွဲတွင် 84 အောက်တွင် ရမှတ်များရှိသည်။

ဥပမာ ၂

ဥယျာဉ်တစ်ခုရှိ အပင်များ၏ အမြင့်သည် ပုံမှန်အားဖြင့် μ = 26.5 လက်မ နှင့် စံသွေဖည် σ = 2.5 လက်မ ဖြင့် ပုံမှန် ဖြန့်ဝေပါသည်။ ခန့်မှန်းခြေအားဖြင့် အပင်အမြင့် ၂၆ လက်မထက် မည်မျှရှိသနည်း။

အဆင့် 1- z-score ကိုရှာပါ။

ဦးစွာ၊ ၂၆ လက်မ အမြင့်နှင့် ဆက်စပ်နေသည့် z-score ကို ရှာတွေ့ပါမည်။

z-score = (x – μ) / σ = (26 – 26.5) / 2.5 = -0.5 / 2.5 = -0.2

အဆင့် 2- z ရမှတ်နှင့် ကိုက်ညီသော ရာခိုင်နှုန်းကို ရှာဖွေရန် z ဇယားကို အသုံးပြုပါ။

ထို့နောက် တန်ဖိုး -0.2 ကို ရှာပါမည်။   ဇယား z တွင်

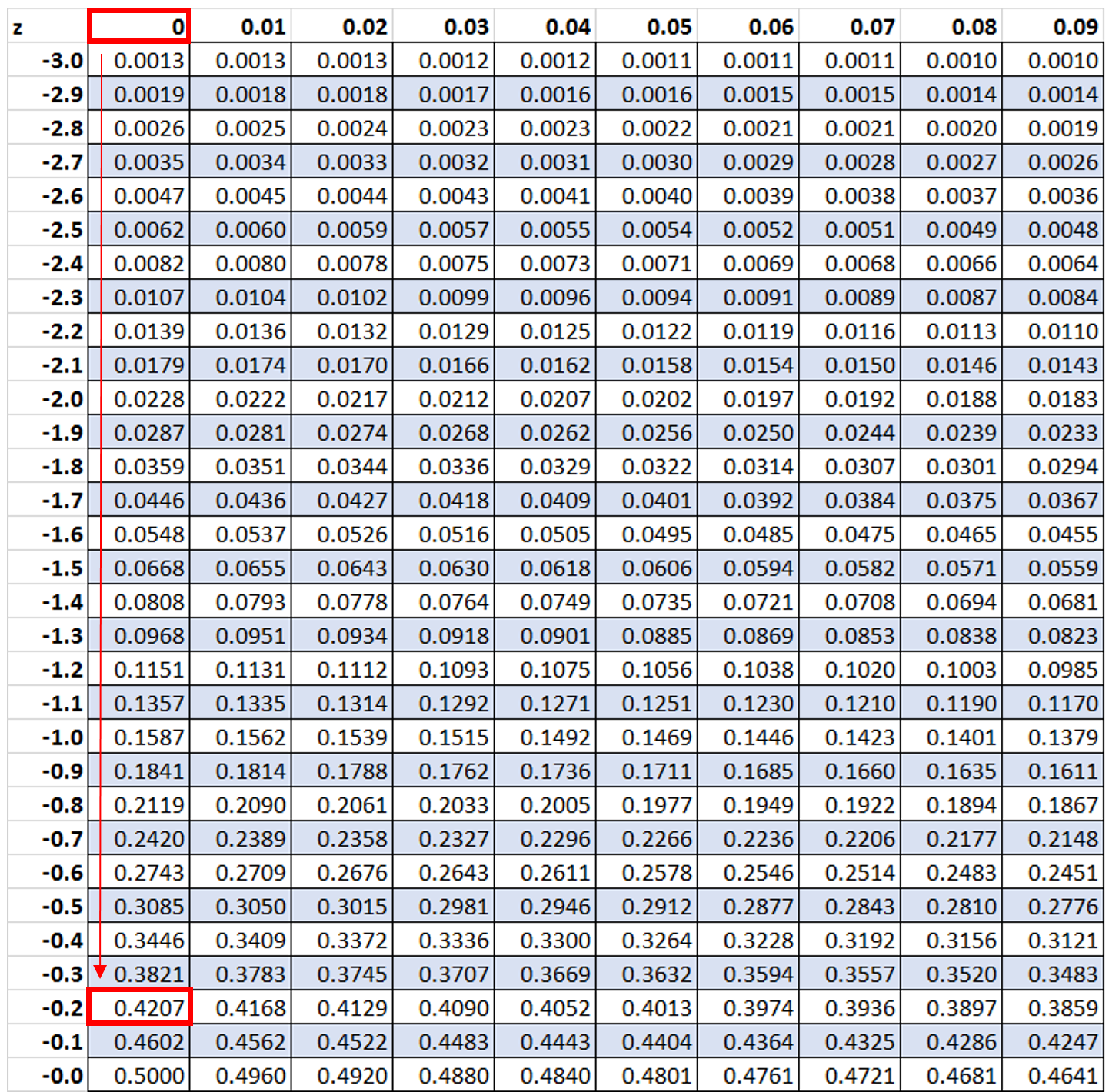
တန်ဖိုးများ၏ 42.07% သည် z-score -0.2 အောက်တွင် ရှိနေသည်ကို ကျွန်ုပ်တို့မြင်သည်။ သို့သော်၊ ဤဥပမာတွင် ဖော်မြူလာ 100% – 42.07% = 57.93% ကို အသုံးပြု၍ မည်သည့်တန်ဖိုးများ၏ ရာခိုင်နှုန်းသည် -0.2 ထက် ကြီးသည် ကို ကျွန်ုပ်တို့ သိလိုပါသည်။

ထို့ကြောင့် ဤဥယျာဉ်ရှိ အပင်များ၏ ခန့်မှန်းခြေ 59.87% သည် 26 လက်မကျော်မြင့်သည်။

ဥပမာ ၃

အချို့သော လင်းပိုင်မျိုးစိတ်များ၏ အလေးချိန်ကို ပုံမှန်အားဖြင့် ပျမ်းမျှအားဖြင့် μ = 400 ပေါင် နှင့် စံသွေဖည်မှု σ = 25 ပေါင် ဖြစ်သည်။ ခန့်မှန်းခြေအားဖြင့် လင်းပိုင်များ၏ အလေးချိန်မှာ ၄၁၀ မှ ၄၂၅ ပေါင်ကြားရှိ သည်။

အဆင့် 1- z-ရမှတ်များကို ရှာပါ။

ပထမဦးစွာ၊ စာအုပ် 410 အုပ်နှင့် 425 စာအုပ်များနှင့်ဆက်စပ်သော z-scores များကိုတွေ့လိမ့်မည်။

z-ရမှတ် 410 = (x – μ) / σ = (410 – 400) / 25 = 10/25 = 0.4

z ရမှတ် 425 = (x – μ) / σ = (425 – 400) / 25 = 25 / 25 = 1

အဆင့် 2- z ရမှတ်တစ်ခုစီနှင့် ကိုက်ညီသည့် ရာခိုင်နှုန်းများကို ရှာဖွေရန် z ဇယားကို အသုံးပြုပါ။

အရင်ဆုံး value 0.4 ကိုရှာပါမယ်။   ဇယား z တွင်

နောက်တစ်ခုကတော့ value 1 ကိုရှာပါမယ်။   ဇယား z တွင်

နောက်ဆုံးတွင်၊ အကြီးဆုံးတန်ဖိုးမှ အသေးငယ်ဆုံးတန်ဖိုးကို နုတ်ပါမည်- 0.8413 – 0.6554 = 0.1859 ။

ထို့ကြောင့်၊ လင်းပိုင်များ၏ 18.59% ခန့်သည် အလေးချိန် 410 နှင့် 425 ပေါင်ကြားရှိသည်။

ထပ်လောင်းအရင်းအမြစ်များ

သာမာန်ဖြန့်ဖြူးမှုမိတ်ဆက်
ပုံမှန်ဖြန့်ဝေဧရိယာဂဏန်းတွက်စက်
Z ရမှတ်ဂဏန်းတွက်စက်