အချိုးအစားနှစ်ခု z စမ်းသပ်မှု- အဓိပ္ပါယ်၊ ဖော်မြူလာနှင့် ဥပမာ

လူဦးရေအချိုးအစားနှစ်ခုကြား ခြားနားချက်ကို စမ်းသပ်ရန်အတွက် two-proportion z-test ကို အသုံးပြုသည်။

ဤသင်ခန်းစာတွင် အောက်ပါတို့ကို ရှင်းပြထားသည်။

• အချိုးနှစ်ဆ z-test ကိုလုပ်ဆောင်ခြင်းအတွက် စေ့ဆော်မှု။
• အချိုးကျ z စမ်းသပ်မှုနှစ်ခု လုပ်ဆောင်ရန်အတွက် ဖော်မြူလာ။
• အချိုးနှစ်ဆ z-test ကို လုပ်ဆောင်ပုံ ဥပမာ။

အချိုးအစားနှစ်ခု Z စမ်းသပ်မှု- လှုံ့ဆော်မှု

ကောင်တီ A တွင် ဥပဒေတစ်ရပ်ရပ်ကို ပံ့ပိုးပေးသည့် နေထိုင်သူအချိုးနှင့် ကောင်တီ B တွင် ဥပဒေကို ပံ့ပိုးပေးသည့် အချိုးအစားအကြား ကွာခြားမှု ရှိမရှိကို ကျွန်ုပ်တို့ သိလိုသည်ဆိုပါစို့။

ခရိုင်တစ်ခုစီတွင် နေထိုင်သူ ထောင်နှင့်ချီရှိသောကြောင့် ခရိုင်တစ်ခုစီတွင် နေထိုင်သူတိုင်းကို လှည့်လည်ကြည့်ရှုပြီး စစ်တမ်းကောက်ယူရန် အချိန်ကုန်ပြီး စျေးကြီးမည်ဖြစ်သည်။

ယင်းအစား၊ ခရိုင်တစ်ခုစီမှ နေထိုင်သူများ၏ ရိုးရှင်းသော ကျပန်းနမူနာကို ယူကာ နမူနာတစ်ခုစီရှိ ဥပဒေ၏ နှစ်သက်ရာအချိုးကို အသုံးပြု၍ ခရိုင်နှစ်ခုကြားရှိ အချိုးအစားအမှန်ကို ခန့်မှန်းရန်-

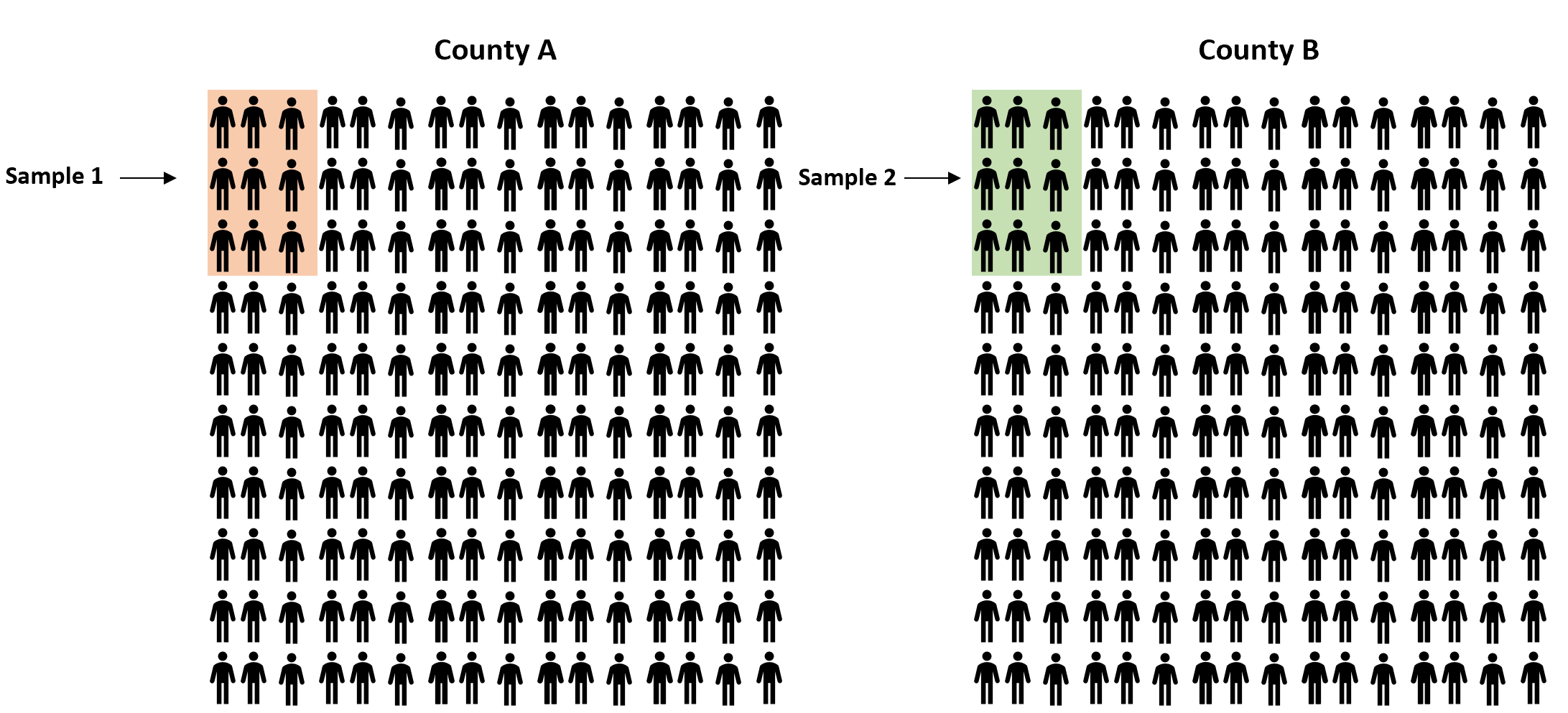
သို့ရာတွင်၊ ဥပဒေအား ထောက်ခံအားပေးသည့် နေထိုင်သူအချိုးသည် နမူနာနှစ်ခုကြား အနည်းဆုံး အနည်းငယ်ကွာခြားလိမ့်မည်ဖြစ်ကြောင်း အာမခံပါသည်။ မေးခွန်းက ဒီကွာခြားချက်က ကိန်းဂဏန်းအရ သိသာထင်ရှားသလား ။ ကံကောင်းထောက်မစွာ၊ အချိုးကျ z-test သည် ကျွန်ုပ်တို့အား ဤမေးခွန်းကို ဖြေနိုင်စေပါသည်။

အချိုးအစားနှစ်ခု Z စမ်းသပ်မှု- ဖော်မြူလာ

အချိုးအစားနှစ်ရပ် z-test သည် အောက်ပါ null hypothesis ကို အမြဲသုံးသည်-

• H ₀ : μ ₁ = μ ₂ (လူဦးရေအချိုးအစား နှစ်ခုသည် ညီမျှသည်)

အခြားယူဆချက်သည် နှစ်ဘက်၊ ဘယ် သို့မဟုတ် ညာဘက် ဖြစ်နိုင်သည်-

• H ₁ (အမြီးနှစ်ကောင်): π ₁ ≠ π ₂ (လူဦးရေအချိုးအစား နှစ်ခုသည် မညီမျှပါ)
• H ₁ (ဘယ်ဘက်): π ₁ < π ₂ (လူဦးရေအချိုးအစား 1 သည် လူဦးရေအချိုးအစား 2 ထက်နည်းသည်)
• H ₁ (ညာဘက်): π ₁ > π ₂ (လူဦးရေအချိုးအစား 1 သည် လူဦးရေ 2 အချိုးအစားထက် ပိုများသည်)

z စမ်းသပ်ကိန်းဂဏန်းကို တွက်ချက်ရန် အောက်ပါဖော်မြူလာကို အသုံးပြုသည်-

z = (p ₁ -p ₂ ) / √ p(1-p)(1/n ₁ +1/n ₂ )

p ₁ နှင့် p ₂ သည် နမူနာအချိုးများ ရှိရာ၊ n ₁ နှင့် n ₂ သည် နမူနာအရွယ်အစားဖြစ်ပြီး p သည် အောက်ပါအတိုင်း တွက်ချက်ထားသော စုစုပေါင်းအချိုးအစားဖြစ်သည်။

p = (p ₁ n ₁ + p ₂ n ₂ )/(n ₁ + n ₂ )

z test statistic နှင့် ကိုက်ညီသော p-value သည် ရွေးချယ်ထားသော အရေးပါမှုအဆင့်ထက် နည်းနေပါက (အများအားဖြင့် ရွေးချယ်မှုများမှာ 0.10၊ 0.05 နှင့် 0.01)၊ ထို့နောက် null hypothesis ကို ငြင်းပယ်နိုင်ပါသည်။

အချိုးနှစ်မျိုးဖြင့် Z စမ်းသပ်မှု – ဥပမာ

ကောင်တီ A တွင် ဥပဒေတစ်ရပ်ရပ်ကို ပံ့ပိုးပေးသည့် နေထိုင်သူအချိုးနှင့် ကောင်တီ B တွင် ဥပဒေကို ပံ့ပိုးပေးသည့် အချိုးအစားအကြား ကွာခြားမှု ရှိမရှိကို ကျွန်ုပ်တို့ သိလိုသည်ဆိုပါစို့။

၎င်းကိုစမ်းသပ်ရန်အတွက်၊ အောက်ပါအဆင့်များကိုအသုံးပြု၍ အရေးပါသောအဆင့် α = 0.05 တွင် အချိုးနှစ်ဆ z-test ကို လုပ်ဆောင်ပါမည်။

အဆင့် 1: နမူနာဒေတာကို စုဆောင်းပါ။

ကျွန်ုပ်တို့သည် ခရိုင်တစ်ခုစီမှ ကျပန်းနမူနာတစ်ခုကို စုဆောင်းပြီး အောက်ပါအချက်အလက်များကို ရယူသည်ဆိုပါစို့။

နမူနာ 1-

• နမူနာအရွယ်အစား n ₁ = 50
• ပညတ္တိပစ္စယော _၁ = ၀.၆၇ အချိုး

နမူနာ 2-

• နမူနာအရွယ်အစား n ₂ = 50
• ပစ္စယော တရားတော် _၂ = ၀.၅၇ အချိုး

အဆင့် 2- ယူဆချက်များကို သတ်မှတ်ပါ။

အောက်ဖော်ပြပါ ယူဆချက်များဖြင့် ကျွန်ုပ်တို့သည် အချိုးကျ z စမ်းသပ်မှုကို လုပ်ဆောင်ပါမည်။

• H ₀ : π ₁ = π ₂ (လူဦးရေအချိုးအစား နှစ်ခု ညီမျှသည်)
• H ₁ : π ₁ ≠ π ₂ (လူဦးရေအချိုးအစား နှစ်ခုသည် မညီပါ)

အဆင့် 3- z စမ်းသပ်စာရင်းအင်းကို တွက်ချက်ပါ။

ပထမဦးစွာ၊ စုစုပေါင်း ပေါင်းစပ်ထားသော အချိုးအစားကို တွက်ချက်ပါမည်။

p = (p ₁ n ₁ + p ₂ n ₂ )/(n ₁ +n ₂ ) = (0.67(50) + 0.57(50))/(50+50) = 0.62

ထို့နောက်၊ ကျွန်ုပ်တို့သည် z စမ်းသပ်ကိန်းဂဏန်းကို တွက်ချက်ပါမည်-

z = (p ₁ -p ₂ ) / √ p(1-p)(1/n ₁ +1/n ₂ ) = (.67-.57) / √ .62(1-.62)(1/50 + 1/50 ) = 1.03

အဆင့် 4- z စမ်းသပ်စာရင်းအင်း၏ p-တန်ဖိုးကို တွက်ချက်ပါ။

P-value Z-score ဂဏန်းတွက်စက်အရ၊ z = 1.03 နှင့်ဆက်စပ်နေသော အမြီးနှစ်စင်း p-value သည် 0.30301 ဖြစ်သည်။

အဆင့် 5: ကောက်ချက်ဆွဲပါ။

ဤ p-value သည် ကျွန်ုပ်တို့၏ အရေးပါမှုအဆင့် α = 0.05 ထက် မနိမ့်သောကြောင့်၊ null hypothesis ကို ငြင်းပယ်ရန် ပျက်ကွက်ပါသည်။ ခရိုင်နှစ်ခုကြားတွင် ဤဥပဒေအား ထောက်ခံသည့် လူဦးရေ အချိုးသည် ကွဲပြားသည်ဟု ဆိုရန် လုံလောက်သော အထောက်အထား မရှိပါ။

မှတ်ချက်- two-proportion Z test calculator ကို အသုံးပြုရုံဖြင့် သင်သည် ဤ two-proportion Z test တစ်ခုလုံးကို လုပ်ဆောင်နိုင်သည်။

ထပ်လောင်းအရင်းအမြစ်များ

အောက်ဖော်ပြပါ သင်ခန်းစာများသည် ကိန်းဂဏန်းဆိုင်ရာဆော့ဖ်ဝဲကို အသုံးပြု၍ နှစ်အချိုးကျ z-test ကို မည်သို့လုပ်ဆောင်ရမည်ကို ရှင်းပြသည်-

Excel တွင် two-proportion Z test ကို မည်သို့လုပ်ဆောင်ရမည်နည်း။
SAS တွင် two-proportion Z test ကို မည်သို့လုပ်ဆောင်ရမည်နည်း။
Proportion Z Test Calculator နှစ်ခု