အကြိမ်ရေ (စာရင်းအင်း)

ဤဆောင်းပါးသည် ကိန်းဂဏန်းစာရင်းအင်းများတွင် ကြိမ်နှုန်း၏သဘောတရားကို ရှင်းပြထားသည်။ ထို့ကြောင့်၊ စာရင်းဇယားများတွင် ကြိမ်နှုန်း၏ အဓိပ္ပါယ်ဖွင့်ဆိုချက်၊ တည်ရှိနေသော ကြိမ်နှုန်းအမျိုးမျိုးနှင့် နောက်ဆုံးတွင် ကြိမ်နှုန်းဇယားကို မည်သို့ဖန်တီးရမည်ကို သင်တွေ့လိမ့်မည်။

စာရင်းအင်းဆိုင်ရာ ကြိမ်နှုန်းဆိုတာဘာလဲ။

စာရင်းဇယားများတွင်၊ ကြိမ်နှုန်း သည် ဒေတာအတွဲတစ်ခုတွင် တန်ဖိုးတစ်ခုပေါ်လာသည့်အကြိမ်အရေအတွက်ဖြစ်သည်။ ရိုးရိုးရှင်းရှင်းပြောရလျှင် ကြိမ်နှုန်းသည် ကိန်းဂဏန်းနမူနာတစ်ခုတွင် တန်ဖိုးတစ်ခုကို ထပ်ခါတလဲလဲပြုလုပ်သည့်အကြိမ်အရေအတွက်ဖြစ်သည်။

ဥပမာအားဖြင့်၊ စစ်တမ်းတစ်ခုတွင် လူငါးဦးသည် ၎င်းတို့၏ နှစ်သက်ရာအရောင်မှာ အပြာရောင်ဟု ဖြေလျှင် အပြာရောင်၏ ကြိမ်နှုန်းသည် 5 နှင့် ညီမျှသည်။

ယေဘူယျအားဖြင့်၊ ကိန်းဂဏန်းစာရင်းအင်းများတွင် f အညွှန်း i သည် တန်ဖိုး i ၏ ကြိမ်နှုန်းကို ကိုယ်စားပြုရန်အတွက် အသုံးပြုသည်၊ ထို့ကြောင့် ကြိမ်နှုန်းအတွက် အမှတ်အသားမှာ _fi ဖြစ်သည်။

ကြိမ်နှုန်းအားလုံး၏ပေါင်းလဒ်သည် နမူနာရှိဒေတာစုစုပေါင်းကိုပေးသည်။ ထို့ကြောင့်၊ စာရင်းအင်းလေ့လာမှုတိုင်းအတွက် အောက်ပါပုံသေနည်းသည် အမြဲတမ်းမှန်ကန်ပါသည်။

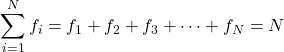
ရွှေ

တန်ဖိုး၏ ကြိမ်နှုန်းဖြစ်သည်။

နှင့်

လေ့လာချက် စုစုပေါင်း အရေအတွက် ဖြစ်ပါသည်။

စာရင်းဇယားများတွင် ကြိမ်နှုန်းအမျိုးအစားများ

စာရင်းဇယားများတွင်၊ မတူညီသော ကြိမ်နှုန်းများ မှာ အောက်ပါအတိုင်းဖြစ်သည်။

• absolute frequency : ကိန်းဂဏန်းနမူနာတစ်ခုတွင် တန်ဖိုးတစ်ခုပေါ်လာသည့်အကြိမ်အရေအတွက်နှင့် ကိုက်ညီသည်။
• စုစည်းမှု အကြွင်းမဲ့ ကြိမ်နှုန်း : တန်ဖိုး ၏ ပကတိ ကြိမ်နှုန်း နှင့် သေးငယ်သော တန်ဖိုး အားလုံး ၏ ပကတိ ကြိမ်နှုန်း များကို ပေါင်းထည့်ခြင်းဖြင့် တွက်ချက်သည် ။
• နှိုင်းရကြိမ်နှုန်း : ၎င်းသည် ဒေတာစုစုပေါင်းအရေအတွက်ဖြင့် ပိုင်းခြားထားသော ပကတိကြိမ်နှုန်းဖြစ်သည်။
• ပွားများသော နှိုင်းရကြိမ်နှုန်း – တန်ဖိုး၏ နှိုင်းရကြိမ်နှုန်း၏ ပေါင်းလဒ်နှင့် အောက်တန်ဖိုးအားလုံး၏ ဆွေမျိုးကြိမ်နှုန်းများနှင့် ညီမျှသည်။

အောက်ဖော်ပြပါကဏ္ဍတွင် ကြိမ်နှုန်းအမျိုးအစားတစ်ခုစီကို မည်ကဲ့သို့ တွက်ချက်ထားသည်ကို ကြည့်ရှုနိုင်ပါသည်။

ကြိမ်နှုန်းဇယား

ပုံမှန်အားဖြင့် စာရင်းဇယားများတွင် အချက်အလက်နမူနာတစ်ခု၏ ကြိမ်နှုန်းတွက်ချက်မှုများကို ကြိမ်နှုန်းဇယားတစ်ခုတွင် အကျဉ်းချုံးထားသည်။ အောက်တွင် အဆင့်ဆင့် ဥပမာပေး၍ လုပ်ပုံလုပ်နည်းကို ကြည့်ရှုနိုင်ပါသည်။

• ကျောင်းသား 30 ရှိသော အတန်းတစ်တန်းတွင် စာရင်းအင်းဘာသာရပ်တွင် ရရှိသော အမှတ်များမှာ အောက်ပါအတိုင်းဖြစ်သည်။ ဒေတာအတွဲ၏ ကြိမ်နှုန်းဇယားကို တည်ဆောက်ပါ။

ဂဏန်းများအားလုံးသည် ကိန်းပြည့်များသာဖြစ်နိုင်သောကြောင့် ၎င်းသည် သီးခြားကွဲလွဲချက်ဖြစ်သည်။ ထို့ကြောင့် အချက်အလက်များကို ကြားကာလအဖြစ် အုပ်စုဖွဲ့ရန် မလိုအပ်ပါ။

ထို့ကြောင့် မတူညီသောတန်ဖိုးတစ်ခုစီသည် အတန်းတစ်ခုဖြစ်သည့် ဇယားတစ်ခုကို တည်ဆောက်ရန် လိုအပ်သည်။ ထို့အပြင်၊ ကျွန်ုပ်တို့သည် ၎င်းကိုလုပ်ဆောင်ရန်အတွက် တန်ဖိုးတစ်ခုစီ၏ ပကတိအကြိမ်ရေကို ရှာဖွေရန် လိုအပ်ပြီး ဒေတာနမူနာတွင် ပေါ်လာသည့်တန်ဖိုး အကြိမ်အရေအတွက်ကို ရိုးရိုးရေတွက်ရန် လိုအပ်သည်။

absolute frequencies အားလုံး၏ပေါင်းလဒ်သည် ဒေတာစုစုပေါင်းအရေအတွက်နှင့် ညီမျှကြောင်း သတိပြုပါ။ ဤစည်းမျဉ်းကို မလေးစားပါက၊ သင်သည် အချို့သော အချက်အလက်များကို ပေးဆောင်ရန် မေ့သွားသည်ဟု ဆိုလိုသည်။

ယခု ကျွန်ုပ်တို့သည် absolute frequency ကို သိရှိပြီး၊ စုစည်းမှု absolute frequency ကို ရှာဖွေရန် လိုအပ်ပါသည်။ ဤတွက်ချက်မှုအတွက် ကျွန်ုပ်တို့တွင် ရွေးချယ်စရာနှစ်ခုရှိသည်- ကျွန်ုပ်တို့သည် တန်ဖိုး၏ ပကတိကြိမ်နှုန်းနှင့် အသေးငယ်ဆုံးတန်ဖိုးများ၏ ပကတိကြိမ်နှုန်းအားလုံးကို ပေါင်းထည့်ခြင်း သို့မဟုတ် ဆန့်ကျင်ဘက်အနေနှင့်၊ ကျွန်ုပ်တို့သည် တန်ဖိုး၏ absolute frequency နှင့် ယခင်တန်ဖိုး၏ ပကတိအကြိမ်ရေကို ပေါင်းထည့်ပါသည်။

နောက်ဆုံးတန်ဖိုး၏ စုစည်းမှု ပကတိအကြိမ်ရေသည် ဒေတာစုစုပေါင်းအရေအတွက်နှင့် အမြဲသက်ဆိုင်သည်၊ တွက်ချက်မှုများမှန်ကန်ကြောင်း အတည်ပြုရန် ဤလှည့်ကွက်ကို သင်အသုံးပြုနိုင်ပါသည်။

ထို့နောက်၊ ကျွန်ုပ်တို့သည် အချက်အလက်စုစုပေါင်းအမှတ် (30) ဖြင့် ပကတိကြိမ်နှုန်းကို ပိုင်းခြားတွက်ချက်ထားသည့် နှိုင်းရကြိမ်နှုန်းကို ဆုံးဖြတ်ရန် လိုအပ်ပါသည်။

နှိုင်းရကြိမ်နှုန်းအားလုံး၏ ပေါင်းလဒ်သည် 1 နှင့် အမြဲညီမျှကြောင်း မှတ်သားထားပါ၊ သို့မဟုတ်ပါက ကြိမ်နှုန်းဇယားရှိ အချို့သော တွက်ချက်မှုများသည် မှားနေသည်ဟု မှတ်သားထားပါ။

နောက်ဆုံးတွင်၊ စုဆောင်းထားသောဆွေမျိုးကြိမ်နှုန်းကိုထုတ်ယူရန်လုံလောက်သည်။ ၎င်းကိုလုပ်ဆောင်ရန်၊ သင်သည် မေးခွန်းရှိတန်ဖိုး၏ နှိုင်းရကြိမ်နှုန်းနှင့် ယခင်နှိုင်းရကြိမ်နှုန်းများအားလုံးကို ပေါင်းထည့်ရမည် သို့မဟုတ်၊ တူညီသောအရာနှင့် ပမာဏဖြစ်သည့် ယခင်စုဆောင်းထားသော ဆွေမျိုးကြိမ်နှုန်းကို ပေါင်းထည့်ရမည်-

အတိုချုပ်အားဖြင့်၊ ပြဿနာရှိသောဒေတာ၏ ကြိမ်နှုန်းများအားလုံးပါသည့် ကြိမ်နှုန်းဇယားသည် အောက်ပါအတိုင်းဖြစ်သည်-