Python တွင် exponential distribution ကိုအသုံးပြုနည်း

ကိန်းဂဏန်းဖြန့်ချီမှုသည် အချို့သောဖြစ်ရပ်တစ်ခုဖြစ်ပေါ်သည်အထိ ကျွန်ုပ်တို့စောင့်ဆိုင်းရမည့်အချိန်ကို နမူနာယူရန် အသုံးပြုသည့် ဖြစ်နိုင်ခြေဖြန့်ဖြူးမှုတစ်ခုဖြစ်သည်။

ကျပန်းပြောင်းလဲနိုင်သော X သည် ထပ်ကိန်းခွဲဝေမှုကို လိုက်နာပါက၊ X ၏ စုစည်းဖြန့်ဝေမှုလုပ်ဆောင်ချက်ကို ရေးသားနိုင်သည်-

F (x; λ) = 1 – e ^–λx

ရွှေ-

• λ- နှုန်းသတ်မှတ်ချက် (λ = 1/μ အဖြစ် တွက်ချက်)
• e- ခန့်မှန်းခြေ ကိန်းသေတစ်ခုသည် 2.718 နှင့် ညီမျှသည်။

ဤသင်ခန်းစာတွင် Python တွင် ကိန်းဂဏန်းဖြန့်ချီမှုကို အသုံးပြုပုံကို ရှင်းပြထားသည်။

ကိန်းဂဏန်းများ ဖြန့်ဖြူးမှုကို မည်သို့ထုတ်လုပ်မည်နည်း။

တိကျသောနှုန်းသတ်မှတ်ချက်နှင့်နမူနာအရွယ်အစားဖြင့် ထပ်ကိန်းခွဲဝေမှုတစ်ခုမှ ကျပန်းတန်ဖိုးများထုတ်လုပ်ရန် Python ရှိ SciPy စာကြည့်တိုက်မှ expon.rvs(စကေး၊ အရွယ်အစား) လုပ်ဆောင်ချက်ကို သင်အသုံးပြုနိုင်သည်-

 from scipy. stats import expo

#generate random values from exponential distribution with rate=40 and sample size=10
expon. rvs (scale= 40 , size= 10 )

array([116.5368323 , 67.23514699, 12.00399043, 40.74580584,
        34.60922432, 2.68266663, 22.70459831, 97.66661811,
         6.64272914, 46.15547298])

မှတ်ချက် – SciPy စာကြည့်တိုက် စာရွက်စာတမ်းအပြည့်အစုံကို ဤနေရာတွင် ရှာတွေ့နိုင်ပါသည်။

Exponential Distribution ကို အသုံးပြု၍ ဖြစ်နိုင်ခြေများကို တွက်ချက်နည်း

အချို့သောရေတွင်းတစ်ခု၏ ပေါက်ကွဲမှုကြားတွင် ပျမ်းမျှ မိနစ်အရေအတွက်သည် မိနစ် 40 ဖြစ်သည်ဟု ယူဆပါ။ မီးတောင်ပေါက်ကွဲမှုအတွက် မိနစ် 50 ထက်နည်းသောစောင့်ဆိုင်းရန် မည်မျှဖြစ်နိုင်မည်နည်း။

ဤပြဿနာကိုဖြေရှင်းရန်အတွက် ကျွန်ုပ်တို့သည် နှုန်းထားသတ်မှတ်ချက်ကို ဦးစွာတွက်ချက်ရန် လိုအပ်သည်-

• λ = 1/µ
• λ = 1/40
• λ = 0.025

CDF ဖော်မြူလာတွင် λ = 0.025 နှင့် x = 50 ကို ချိတ်ဆက်နိုင်သည်-

• P(X ≤ x) = 1 – e ^-λx
• P(X ≤ 50) = 1 – e ^-0.025(50)
• P(X ≤ 50) = 0.7135

နောက်တစ်ကြိမ် မီးတောင်ပေါက်ကွဲမှုအတွက် မိနစ် 50 ထက်နည်းသော စောင့်ဆိုင်းရမည့် ဖြစ်နိုင်ခြေမှာ 0.7135 ဖြစ်သည်။

ဤပြဿနာကို Python တွင်ဖြေရှင်းရန် SciPy ၏ expon.cdf() လုပ်ဆောင်ချက်ကို အသုံးပြုနိုင်သည်။

 from scipy. stats import expo

#calculate probability that x is less than 50 when mean rate is 40
expon. cdf (x=50, scale=40)

0.7134952031398099

နောက်တစ်ကြိမ် မီးတောင်ပေါက်ကွဲမှုအတွက် မိနစ် 50 ထက်နည်းသော စောင့်ဆိုင်းရမည့် ဖြစ်နိုင်ခြေမှာ 0.7135 ဖြစ်သည်။

၎င်းသည် ကျွန်ုပ်တို့ကိုယ်တိုင်တွက်ချက်ထားသော တန်ဖိုးနှင့် ကိုက်ညီပါသည်။

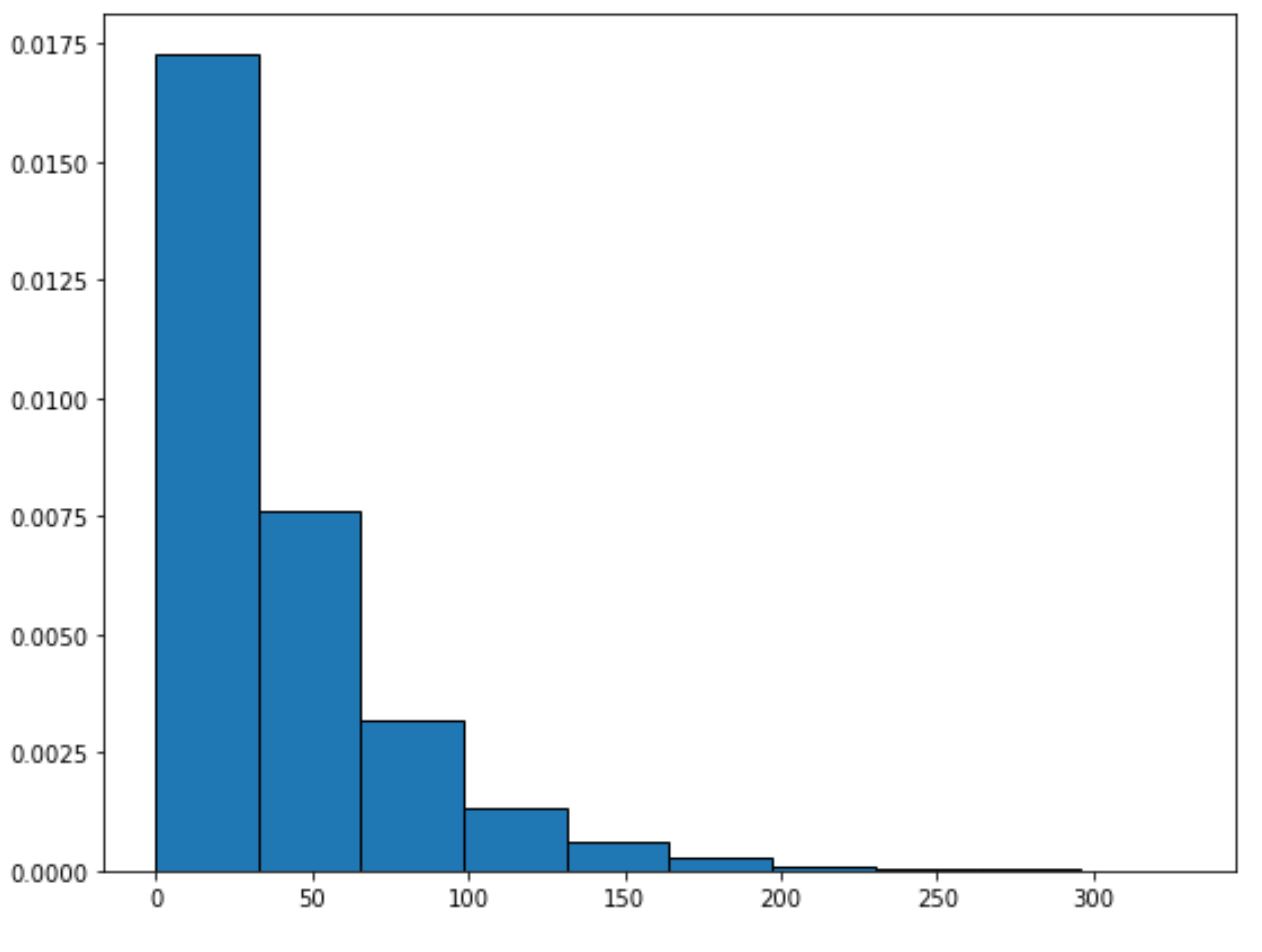
ထပ်ကိန်းခွဲဝေငှမှုကို ဘယ်လိုဆွဲမလဲ။

ပေးထားသောနှုန်းထားသတ်မှတ်ချက်တစ်ခုဖြင့် ထပ်ကိန်းခွဲဝေမှုကို ကြံစည်ရန် အောက်ပါ syntax ကို သင်အသုံးပြုနိုင်သည်-

 from scipy. stats import expo
import matplotlib. pyplot as plt

#generate exponential distribution with sample size 10000
x = expon. rvs (scale= 40 ,size= 10000 )

#create plot of exponential distribution
plt. hist (x, density= True , edgecolor=' black ')

ထပ်လောင်းအရင်းအမြစ်များ

အောက်ပါ သင်ခန်းစာများသည် Python တွင် အခြားသော အသုံးများသော ဖြန့်ဝေမှုများကို အသုံးပြုနည်းကို ရှင်းပြသည်-

Python တွင် Poisson ဖြန့်ဖြူးမှုကို အသုံးပြုနည်း
Python တွင် t distribution ကိုအသုံးပြုနည်း
Python တွင် Uniform Distribution ကိုအသုံးပြုနည်း