Random variable တွေက ဘာတွေလဲ။

ကျပန်း variable ၊ ယေဘုယျအားဖြင့် X ကို ရည်ညွှန်းသည့် ကိန်းရှင်တစ်ခုဖြစ်ပြီး ဖြစ်နိုင်ချေတန်ဖိုးများသည် ကျပန်းလုပ်ငန်းစဉ်တစ်ခု၏ရလဒ်များဖြစ်သည်။

ကျပန်း variable နှစ်မျိုးရှိပါတယ်- discrete နှင့် စဉ်ဆက်မပြတ် ။

သီးသန့်ကျပန်း ကိန်းရှင်များ

သီးခြားကျပန်း ကိန်းရှင် သည် 0၊ 1၊ 2၊ 3၊ 4၊ 5…100၊ 1 သန်း စသည်တို့ကဲ့သို့ ကွဲပြားသော တန်ဖိုးများကို ရေတွက်နိုင်သော အရေအတွက်ကိုသာ ယူနိုင်သည်။ ဤသည်မှာ သီးခြားကျပန်း ကိန်းရှင်များ၏ ဥပမာအချို့ဖြစ်သည်။

• အကြွေစေ့တစ်ခုသည် အကြိမ် 20 ကြိမ်ခံရပြီးနောက် အမြီးပေါက်သွားသည့် အကြိမ်အရေအတွက်။
• အကြိမ် 100 လှိမ့်ခံရပြီးနောက် သေဆုံးသည့်အကြိမ်အရေအတွက်သည် နံပါတ် (၄) တွင် ရှိသည်။
• ဝစ်ဂျက် 50 တစ်ဘူးတွင် ချွတ်ယွင်းနေသော ဝစ်ဂျက်များ အရေအတွက်။

ခွဲခြမ်းစိတ်ဖြာသောကျပန်းကိန်းရှင်အတွက် ဖြစ်နိုင်ခြေဖြန့်ဝေမှုသည် အချို့သောတန်ဖိုးများပေါ်တွင်ကျပန်းကိန်းရှင်၏ဖြစ်နိုင်ခြေကိုပြောပြသည်။

ဥပမာအားဖြင့်၊ ကျွန်ုပ်တို့သည် တရားမျှတသော အံစာတုံးကို တစ်ခါတည်း လှိမ့်လိုက်သည်ဆိုပါစို့။ အကယ်၍ ကျွန်ုပ်တို့သည် ကိန်းဂဏန်းတစ်ခုပေါ်တွင် သေဆုံးမှုဖြစ်နိုင်ခြေကို X ကိုဖော်ပြခွင့်ပြုပါက၊ ဖြစ်နိုင်ခြေဖြန့်ဝေမှုကို အောက်ပါအတိုင်း ရေးသားနိုင်သည်။

• P(X=1): 1/6
• P(X=2): 1/6
• P(X=3): 1/6
• P(X=4): 1/6
• P(X=5): 1/6
• P(X=6): 1/6

မှတ်ချက် –

ဖြစ်နိုင်ခြေ ဖြန့်ဝေမှု မှန်ကန်ရန်အတွက်၊ ၎င်းသည် အောက်ပါစံနှုန်းနှစ်ခုကို ဖြည့်ဆည်းပေးရမည်-

1. ရလဒ်တစ်ခုစီ၏ဖြစ်နိုင်ခြေသည် 0 နှင့် 1 ကြားရှိရပါမည်။

2. ဖြစ်နိုင်ခြေအားလုံး၏ပေါင်းလဒ်သည် 1 အထိ ပေါင်းရပါမည်။

Die roll အတွက် ဖြစ်နိုင်ခြေ ဖြန့်ဖြူးမှုသည် ဤစံနှုန်းနှစ်ခုလုံးကို ကျေနပ်စေသည်-

1. ရလဒ်တစ်ခုစီ၏ ဖြစ်နိုင်ခြေသည် 0 နှင့် 1 ကြားဖြစ်သည်။

2. ဖြစ်နိုင်ခြေအားလုံး၏ပေါင်းလဒ်သည် 1 အထိ ပေါင်းထည့်သည်။

ဖြစ်နိုင်ခြေ ဖြန့်ဖြူးမှုကို မြင်ယောင်ရန် ဟီစတိုဂရမ်ကို အသုံးပြုနိုင်သည်။

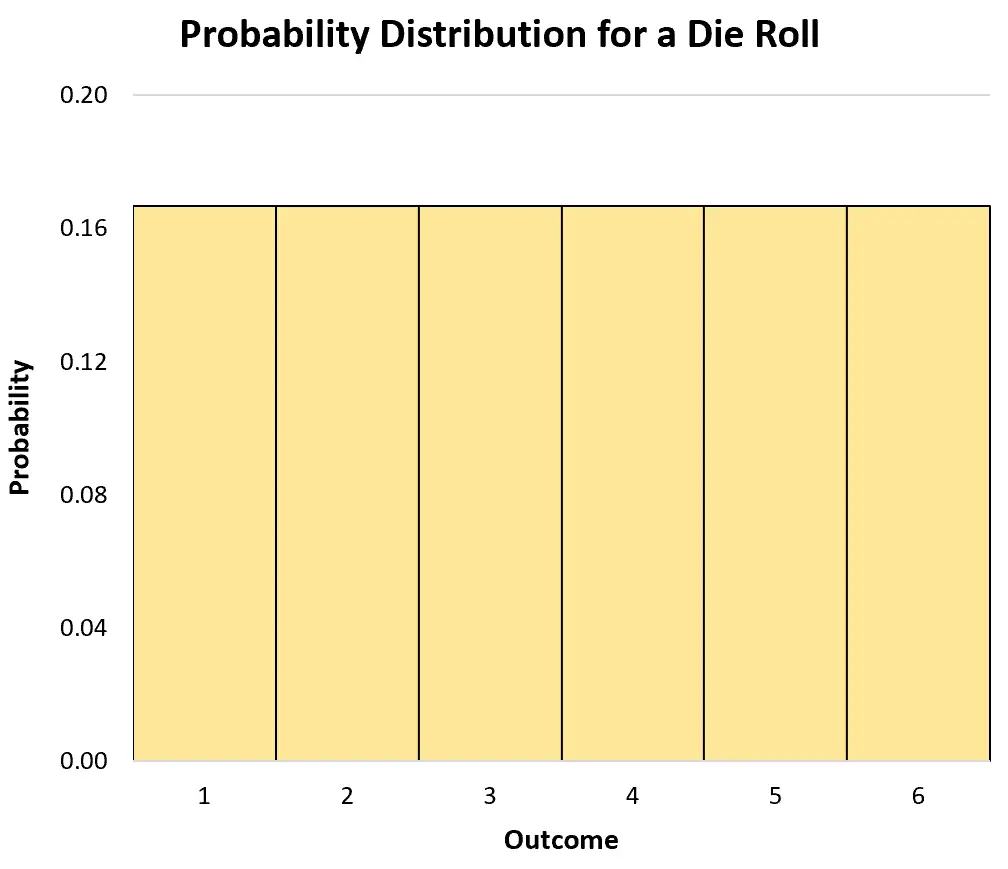
သီးခြားကျပန်းကိန်းရှင်တစ်ခုအတွက် စုစည်းဖြစ်နိုင်ခြေဖြန့်ဝေမှုသည် ကိန်းရှင်သည် အချို့သောတန်ဖိုးထက် ညီမျှသော သို့မဟုတ် လျော့နည်းသော တန်ဖိုးတစ်ခုအပေါ် ကိန်းရှင်၏ဖြစ်နိုင်ခြေကို ပြောပြသည်။

ဥပမာအားဖြင့်၊ သေရည်လိပ်တစ်ခုအတွက် တိုးပွားလာနိုင်သည့် ဖြစ်နိုင်ခြေဖြန့်ဝေမှုသည် အောက်ပါအတိုင်းဖြစ်မည်-

• P(X≤1): 1/6
• P(X≤2): 2/6
• P(X≤3): 3/6
• P(X≤4): 4/6
• P(X≤5): 5/6
• P(X≤6): 6/6

တစ်ခု သို့မဟုတ် ထိုထက်နည်းသော ကိန်းဂဏာန်းတစ်ခုသို့ ဆင်းသက်ရန် အခွင့်အလမ်းသည် ရိုးရိုး 1/6 ဖြစ်သောကြောင့်၊

နှစ်ခု သို့မဟုတ် အောက်သို့ ဆင်းသက်ခြင်း၏ ဖြစ်နိုင်ခြေမှာ P(X=1) + P(X=2) = 1/6 + 1/6 = 2/6 ဖြစ်သည်။

အလားတူ၊ သုံးခု သို့မဟုတ် ထို့ထက်နည်းသော ဆင်းသက်နိုင်ခြေသည် P(X=1) + P(X=2) + P(X=3) = 1/6 + 1/6 + 1/6 = 3/6၊ ဒါပေါ်မှာ။

တိုးပွားလာနိုင်သော ဖြစ်နိုင်ခြေဖြန့်ဝေမှုကို မြင်ယောင်ရန် ဟီစတိုဂရမ်ကိုလည်း အသုံးပြုနိုင်သည်။

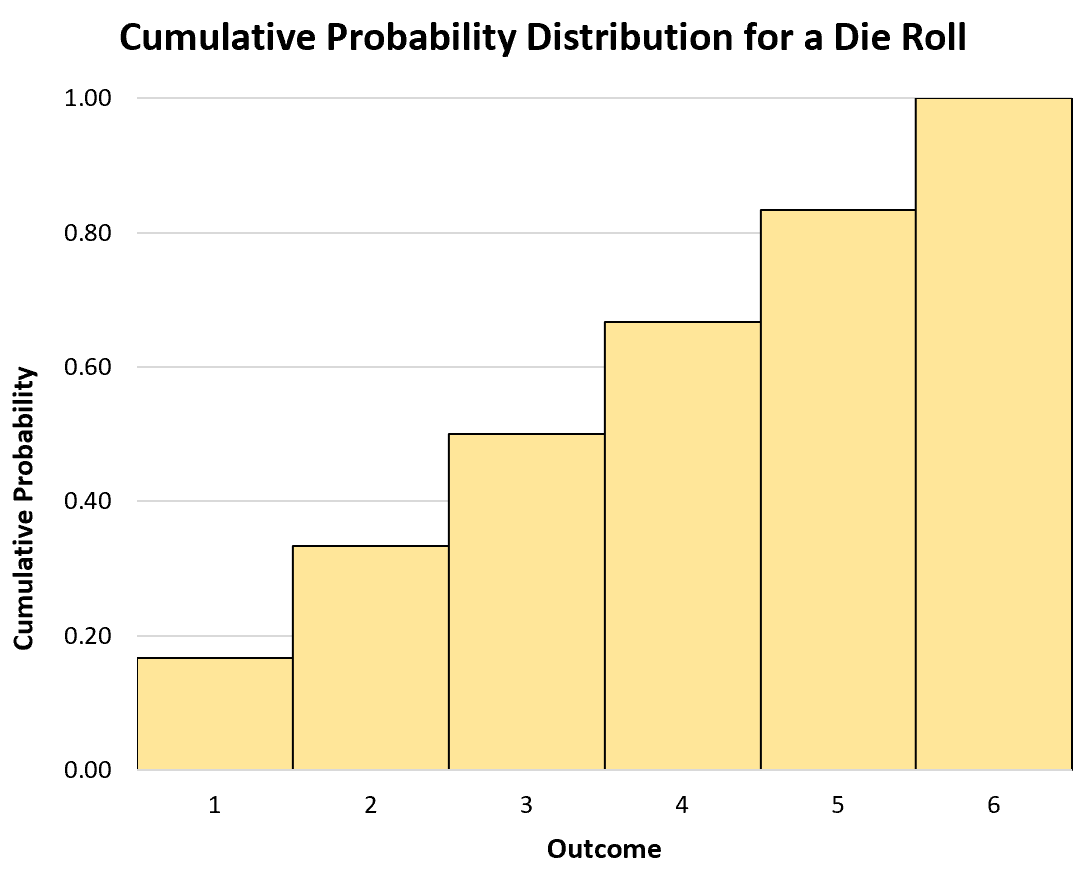
အဆက်မပြတ် ကျပန်းပြောင်းလဲနိုင်သော ကိန်းရှင်များ

စဉ်ဆက်မပြတ် ကျပန်းပြောင်းလဲနိုင်သောကိန်းရှင် သည် ဖြစ်နိုင်ချေတန်ဖိုးများစွာကို အကန့်အသတ်မရှိယူဆောင်နိုင်သော ကိန်းရှင်တစ်ခုဖြစ်သည်။ ဤသည်မှာ စဉ်ဆက်မပြတ် ကျပန်းပြောင်းလဲနိုင်သော ဥပမာအချို့ဖြစ်သည်။

• တိရစ္ဆာန်၏အလေးချိန်
• လူတစ်ဦး၏အမြင့်
• မာရသွန်ပြေးဖို့ အချိန်လိုတယ်။

ဥပမာအားဖြင့် လူတစ်ဦး၏ အရပ်သည် 60.2 လက်မ၊ 65.2344 လက်မ၊ 70.431222 လက်မ၊ စသည်တို့ ဖြစ်နိုင်သည်။ အရွယ်အစားအတွက် ဖြစ်နိုင်ချေတန်ဖိုးများ အနန္တပမာဏရှိပါသည်။

အထွေထွေစည်းမျဉ်း-

ရလဒ်အရေအတွက်ကို သင် ရေတွက် နိုင်လျှင် သင်သည် သီးခြားကျပန်းပြောင်းလဲမှုတစ်ခုဖြင့် လုပ်ဆောင်နေပါသည် – ဥပမာအားဖြင့်၊ အကြွေစေ့ခေါင်းပေါ်တက်လာသည့်အကြိမ်အရေအတွက်ကို ရေတွက်ခြင်း။

ဒါပေမယ့် ရလဒ်ကို တိုင်းတာ နိုင်ရင်၊ ဥပမာ- အရပ်၊ အလေးချိန်၊ အချိန် စတာတွေကို တိုင်းတာတဲ့ စဉ်ဆက်မပြတ် ကျပန်းပြောင်းလဲမှုတစ်ခုနဲ့ လုပ်ဆောင်နေပါတယ်။

ကျပန်းကိန်းရှင်သည် စဉ်ဆက်မပြတ် ကျပန်းကိန်းရှင်အတွက် ဖြစ်နိုင်ခြေဖြန့်ဝေမှုသည် အချို့သောတန်ဖိုးများပေါ်တွင် ကျပန်းပြောင်းလဲခြင်းဖြစ်နိုင်ခြေကို ပြောပြသည်။

သို့သော်၊ သီးခြားကျပန်းကိန်းရှင်များအတွက် ဖြစ်နိုင်ခြေဖြန့်ဝေခြင်းနှင့်မတူဘဲ၊ စဉ်ဆက်မပြတ်ကျပန်းကိန်းရှင်တစ်ခုအတွက် ဖြစ်နိုင်ခြေဖြန့်ဝေမှုကို ကိန်းရှင်သည် တန်ဖိုးများစွာ အကွာအဝေး တွင် ယူဆောင်သည့်ဖြစ်နိုင်ခြေကို ပြောပြရန်အတွက်သာ ကျွန်ုပ်တို့ကို အသုံးပြုနိုင်သည်။

ဥပမာအားဖြင့်၊ စားသောက်ဆိုင်တစ်ခုမှ ဟမ်ဘာဂါသည် လေးပုံတစ်ပုံပေါင် (0.25 ပေါင်) အလေးချိန်ရှိနိုင်ခြေကို ကျွန်ုပ်တို့ သိလိုသည်ဆိုပါစို့။ အလေးချိန် သည် စဉ်ဆက်မပြတ် ပြောင်းလဲနိုင်သော ဖြစ်သောကြောင့်၊ ၎င်းသည် အကန့်အသတ်မဲ့ တန်ဖိုးများကို ယူနိုင်သည်။

ဥပမာအားဖြင့်၊ ပေးထားသော ဟမ်ဘာဂါတစ်ခုသည် အမှန်တကယ် အလေးချိန် 0.250001 ပေါင် သို့မဟုတ် 0.24 ပေါင် သို့မဟုတ် 0.2488 ပေါင် ရှိသည်။ ပေးထားသော ဟမ်ဘာဂါသည် 0.25 ပေါင် အတိအကျ အလေးချိန်ရှိမည့် ဖြစ်နိုင်ခြေသည် အခြေခံအားဖြင့် သုညဖြစ်သည်။

ထို့ကြောင့် ဟမ်ဘာဂါသည် 0.25 ပေါင်အောက်၊ 0.25 ပေါင်ထက် ပိုလေးသည် သို့မဟုတ် အတိုင်းအတာတစ်ခုကြား (ဥပမာ 0.23 ပေါင် နှင့် 0.27 ပေါင်ကြား) ဖြစ်နိုင်ခြေကို ပြောပြရန် ဖြစ်နိုင်ခြေ ဖြန့်ဖြူးမှုကိုသာ အသုံးပြုနိုင်သည်။

ထပ်လောင်းအရင်းအမြစ်များ

အောက်ဖော်ပြပါ သင်ခန်းစာများသည် ကျပန်းပြောင်းလဲနိုင်သော အချက်အလက်များကို ပေးဆောင်သည်-

iid random variable တွေက ဘာတွေလဲ။
လက်တွေ့ဘဝတွင် ကျပန်းပြောင်းလဲနိုင်သော ဥပမာ ၁၀ ခု