ကွဲလွဲနေသော အဖြစ်အပျက်များကား အဘယ်နည်း။ (အဓိပ္ပါယ်နှင့် ဥပမာများ)
ကွဲလွဲနေသောဖြစ်ရပ်များ သည် တစ်ချိန်တည်းတွင် မဖြစ်ပေါ်နိုင်သော အဖြစ်အပျက်များဖြစ်သည်။
ဖြစ်နိုင်ခြေရှိသော အမှတ်အသားဖြင့် ရေးထားသော ဖြစ်ရပ်များသည် A နှင့် B တို့၏ လမ်းဆုံ သည် သုညဖြစ်လျှင် ကွဲလွဲနေပါသည်။ ၎င်းကို အောက်ပါအတိုင်း ရေးသားနိုင်သည်။
- P(A နှင့် B) = 0
- P(A∩B) = 0
ဥပမာအားဖြင့်၊ ကျွန်ုပ်တို့သည် ကုန်းပတ်တစ်ခုမှ ကတ်တစ်ခုကို ကျပန်းရွေးချယ်သည်ဆိုပါစို့။ အဖြစ်အပျက် A သည် ကတ်သည် စပယ် သို့မဟုတ် ကလပ်တစ်ခု ဖြစ်ပါစေ၊ ကတ်သည် နှလုံးသား သို့မဟုတ် စိန်ဖြစ်ပါစေ ဖြစ်ရပ် B ဖြစ်ပါစေ။
ဖြစ်ရပ်များအတွက်နမူနာနေရာကို အောက်ပါအတိုင်း ကျွန်ုပ်တို့ သတ်မှတ်ပါမည်-
- A = {Spade၊ Club}
- B = {နှလုံးသား၊ စိန်}
နမူနာယူထားသော နေရာနှစ်ခုကြား ထပ်နေခြင်းမရှိကြောင်း သတိပြုပါ။ ထို့ကြောင့် အဖြစ်အပျက် A နှင့် B တို့သည် တစ်ချိန်တည်းတွင် မဖြစ်ပေါ်နိုင်သောကြောင့် ကွဲလွဲနေသော အဖြစ်အပျက်များဖြစ်သည်။
မှတ်ချက်- ကွဲလွဲနေသောဖြစ်ရပ်များကိုလည်း သီးသန့်ဟု ဆိုပါသည်။
ကွဲလွဲနေသောဖြစ်ရပ်များ ဥပမာများ
ဤသည်မှာ ကွဲလွဲနေသော အဖြစ်အပျက်များ၏ နောက်ထပ်ဥပမာအချို့ဖြစ်သည်။
ဥပမာ 1- ဆွဲပါ။
အကြွေစေ့ကိုလှန်တယ်ဆိုပါစို့။ အကြွေစေ့ခေါင်းများပေါ်တွင် အကြွေစေ့ကျသည့် အဖြစ်အပျက် A ဖြစ်ပါစေ၊ ဖြစ်ရပ် B သည် အကြွေစေ့ခေါင်းပေါ်ကျသည့် အဖြစ်အပျက်ဖြစ်ပါစေ။
Event A နှင့် Event B နှစ်ခုလုံးသည် တစ်ချိန်တည်းတွင် မဖြစ်ပေါ်နိုင်သောကြောင့် ကွဲလွဲနေပါသည်။ ဒင်္ဂါးသည် ဦးခေါင်း သို့မဟုတ် အမြီးပေါ် မတက်နိုင်ပါ။
ဥပမာ 2- အန်စာတုံးများ လှိမ့်ခြင်း။
မင်းသေတယ်ဆိုပါစို့။ အဖြစ်အပျက် A သည် ကိန်းဂဏန်းတစ်ခုပေါ်တွင် သေဆုံးသည့်ဖြစ်ရပ်ဖြစ်ပါစေ၊ အဖြစ်အပျက် B သည် ကိန်းဂဏန်းတစ်ခုပေါ်တွင် သေဆုံးသည့်ဖြစ်ရပ်ဖြစ်ပါစေ။
Event A နှင့် Event B နှစ်ခုလုံးသည် တစ်ချိန်တည်းတွင် မဖြစ်ပေါ်နိုင်သောကြောင့် ကွဲလွဲနေပါသည်။ အန်စာတုံးသည် ကိန်းဂဏန်းတစ်ခု နှင့် ကိန်းဂဏန်းတစ်ခုအပေါ်တွင် ကျရောက်နိုင်မည်မဟုတ်ပေ။
ဥပမာ 3- Pro Bowl တည်နေရာ
NFL သည် Pro Bowl ကို လက်ခံကျင်းပရန် တည်နေရာကို ရွေးချယ်လိုသည်ဆိုပါစို့။ သူတို့သည် မိုင်ယာမီနှင့် ဆန်ဒီယေဂိုရှိ ရွေးချယ်မှုများကို ကျဉ်းမြောင်းစေခဲ့သည်။ သူတို့သည် ဦးထုပ်တစ်ခုတွင် နာမည်နှစ်ခုကို ထည့်ကာ တစ်လုံးကို ကျပန်းရွေးချယ်သည်။ Event A သည် မိုင်ယာမီအတွက် ၎င်းတို့ရွေးချယ်ထားသော ပွဲဖြစ်ပြီး Event B သည် ၎င်းတို့ San Diego အတွက် ရွေးချယ်ထားသော ပွဲဖြစ်သည်ဟု ယူဆကြပါစို့။
Event A နှင့် Event B နှစ်ခုလုံးသည် တစ်ချိန်တည်းတွင် မဖြစ်ပေါ်နိုင်သောကြောင့် ကွဲလွဲနေပါသည်။ Miami နှင့် San Diego နှစ်ခုလုံးကို ရွေး၍မရပါ။
ကွဲလွဲနေသောဖြစ်ရပ်များကိုကြည့်ပါ။
ကွဲလွဲနေသောဖြစ်ရပ်များကိုမြင်ယောင်ရန် အသုံးဝင်သောနည်းလမ်းမှာ Venn ပုံကြမ်းကိုဖန်တီးခြင်းဖြစ်သည်။
ဖြစ်ရပ်နှစ်ခု ကွဲလွဲနေ ပါက Venn ပုံတွင် လုံးဝထပ်နေမည်မဟုတ်ပါ။
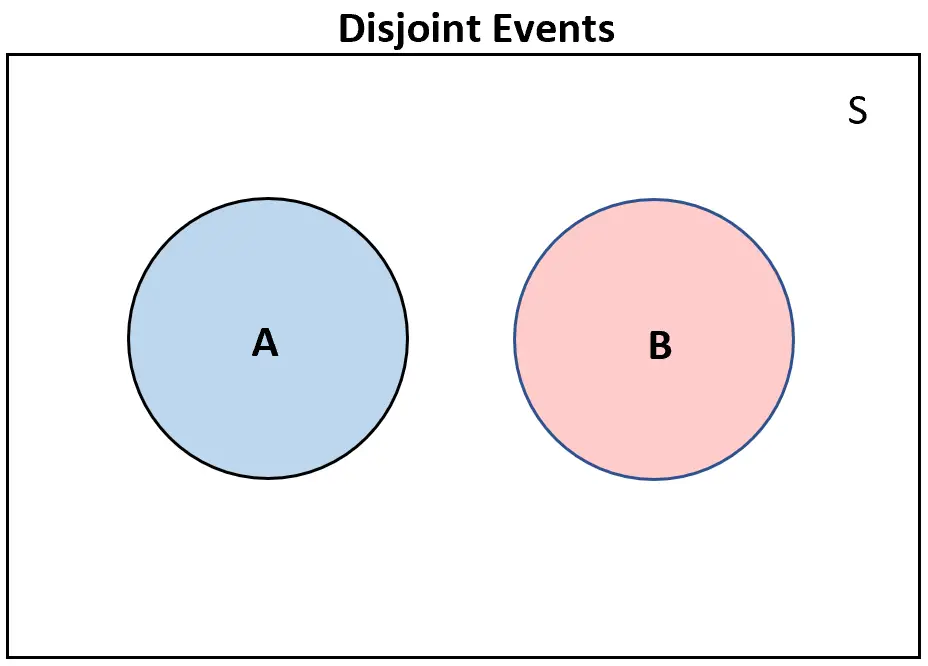
အပြန်အလှန်အားဖြင့်၊ ဖြစ်ရပ်နှစ်ခု မကွဲလွဲပါ က Venn diagram တွင် အနည်းဆုံး အချို့ထပ်နေလိမ့်မည်-
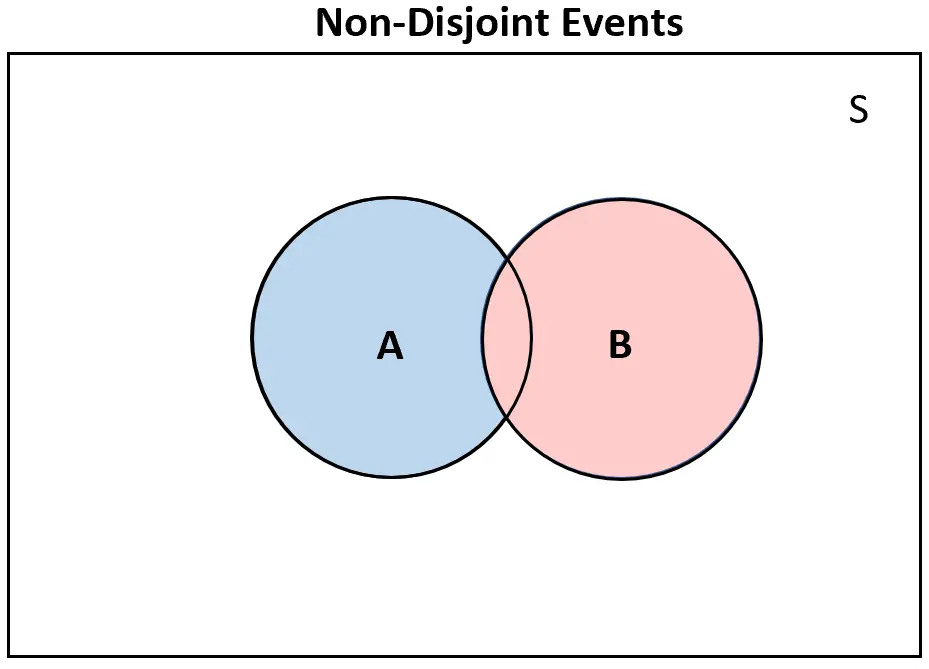
ကွဲလွဲနေသော ဖြစ်ရပ်များ ဖြစ်နိုင်ခြေ
အစောပိုင်းတွင် ဖော်ပြခဲ့သည့်အတိုင်း ဖြစ်ရပ်နှစ်ခုလုံး ကွဲလွဲနေပါက ၎င်းတို့နှစ်ခုလုံးသည် တစ်ချိန်တည်းတွင် ဖြစ်ပွားနိုင်ခြေသည် သုညဖြစ်သည်။
- P(A∩B) = 0
အလားတူပင်၊ အဖြစ်အပျက်တစ်ခု ချင်းစီ ၏ ဖြစ်နိုင်ခြေများကို ပေါင်းထည့်ခြင်းဖြင့် အဖြစ်အပျက်တစ်ခုချင်းစီ၏ ဖြစ်နိုင်ခြေကို တွက်ချက်နိုင်သည်။
- P(A∪B) = P(A) + P(B)
ဥပမာအားဖြင့်၊ event A သည် 1 သို့မဟုတ် 2 တွင်သေဆုံးသည့်ဖြစ်ရပ်ဖြစ်ပါစေ အဖြစ်အပျက် B သည် 5 သို့မဟုတ် 6 တွင်သေဆုံးသည့်ဖြစ်ရပ်ဖြစ်ပါစေ။
ဖြစ်ရပ်များအတွက် နမူနာနေရာကို အောက်ပါအတိုင်း ကျွန်ုပ်တို့ သတ်မှတ်ပါမည်-
- A = {1၊ 2}
- B = {5, 6}၊
အဖြစ်အပျက် A သို့မဟုတ် အဖြစ်အပျက် B ၏ ဖြစ်နိုင်ခြေကို ကျွန်ုပ်တို့ တွက်ချက်သည်-
- P(A∪B) = P(A) + P(B)
- P(A∪B) = 2/6 + 2/6
- P(A∪B) = 4/6 = 2/3
ဖြစ်ရပ် A သို့မဟုတ် ဖြစ်ရပ် B ၏ ဖြစ်နိုင်ခြေသည် 2/3 ဖြစ်သည်။
ထပ်လောင်းအရင်းအမြစ်များ
အောက်ဖော်ပြပါ သင်ခန်းစာများတွင် အခြားအဖြစ်များသော ဖြစ်နိုင်ခြေအကြောင်းအရာများကို ရှင်းပြပေးသည်-
A သို့မဟုတ် B ၏ဖြစ်နိုင်ခြေကို မည်သို့ရှာရမည်နည်း။
A နှင့် B ၏ဖြစ်နိုင်ခြေကိုမည်သို့ရှာဖွေနည်း- ဥပမာများဖြင့်
စုစုပေါင်းဖြစ်နိုင်ခြေဥပဒေ- အဓိပ္ပါယ်ဖွင့်ဆိုချက်နှင့် ဥပမာများ