ကွဲလွဲမှု

အားဖြင့် Benjamin Anderson ဩဂုတ် 5, 2023 စာရင်းအင်းများ 0 မှတ်ချက်များ

ဤဆောင်းပါးတွင် ကွဲလွဲမှုဟုလည်း ခေါ်သော ကွဲလွဲမှု နှင့် ၎င်းကို မည်ကဲ့သို့ တွက်ချက်ကြောင်း ရှင်းပြပါသည်။ ကွဲလွဲမှု ဖော်မြူလာ၊ ကွဲလွဲမှု တွက်ချက်ခြင်း၏ ခိုင်မာသော ဥပမာတစ်ခုကို တွေ့ရမည်ဖြစ်ပြီး၊ ထို့အပြင်၊ အွန်လိုင်းဂဏန်းတွက်စက်ဖြင့် သတ်မှတ်ဒေတာများ၏ ကွဲလွဲမှုကို တွက်ချက်နိုင်မည်ဖြစ်သည်။

၎င်းကို မတူညီသောနည်းလမ်းဖြင့် လုပ်ဆောင်သောကြောင့် အုပ်စုဖွဲ့ထားသောဒေတာ၏ ကွဲလွဲမှုကို မည်သို့ရှာဖွေရမည်ကို ကျွန်ုပ်တို့လည်း ပြသထားသည်။ နောက်ဆုံးတွင်၊ လူဦးရေကွဲလွဲမှုနှင့် နမူနာကွဲလွဲမှုအကြား ခြားနားချက်၊ ကွဲလွဲမှုနှင့် စံသွေဖည်မှုကြား ခြားနားချက်နှင့် ဤကိန်းဂဏန်းဆိုင်ရာ တိုင်းတာမှု၏ ဂုဏ်သတ္တိများကို ကျွန်ုပ်တို့ သင်ပေးပါသည်။

ကွဲလွဲမှုဆိုတာဘာလဲ။

ကိန်းဂဏန်းစာရင်းဇယားများတွင်၊ ကွဲလွဲမှုသည် ကျပန်းကိန်းရှင်၏ ကွဲပြားမှုကို ညွှန်ပြသည့် ပြန့်ကျဲမှုအတိုင်းအတာတစ်ခုဖြစ်သည်။ ကွဲလွဲချက်သည် အကြွင်းအကျန်များ၏ နှစ်ထပ်ကိန်းများ၏ ပေါင်းလဒ်နှင့် ညီမျှသည်။

ကိန်းဂဏန်းအချက်အလက်အချက်တစ်ခု၏တန်ဖိုးနှင့် ဒေတာအစုံ၏ပျမ်းမျှအကြား ခြားနားချက်အဖြစ် ကျန်ရှိသောအရာကို နားလည်ကြောင်း သတိရပါ။

ဖြစ်နိုင်ခြေသီအိုရီတွင်၊ ကွဲလွဲမှုအတွက်သင်္ကေတသည် ဂရိအက္ခရာ sigma နှစ်ထပ်ကိန်း (σ ² ) ဖြစ်သည်။ Var(X) အဖြစ်လည်း အများအားဖြင့် ကိုယ်စားပြုသော်လည်း X သည် ကွဲလွဲမှုကို တွက်ချက်သည့် ကျပန်း variable ဖြစ်သည်။

ယေဘူယျအားဖြင့်၊ ကျပန်းကိန်းရှင်တစ်ခု၏ ကွဲလွဲမှုတန်ဖိုးကို အဓိပ္ပာယ်ပြန်ဆိုခြင်းသည် ရိုးရှင်းပါသည်။ ကွဲလွဲမှုတန်ဖိုး ကြီးလေ၊ ဒေတာ ပြန့်ကျဲလေလေ ဖြစ်သည်။ အပြန်အလှန်အားဖြင့်၊ ကွဲလွဲမှုတန်ဖိုး သေးငယ်လေ၊ ဒေတာစီးရီးတွင် ကွဲလွဲမှုနည်းလေဖြစ်သည်။ သို့ရာတွင်၊ ကွဲလွဲမှုတန်ဖိုးကို လှည့်စားနိုင်သောကြောင့် ကွဲလွဲမှုကို ဘာသာပြန်ဆိုရာတွင် အစွန်းကွက်များကို သတိထားရပါမည်။

ကွဲလွဲမှု၊ ကွဲလွဲမှုဟု သတ်မှတ်သည့် အခြားတိုင်းတာမှုများမှာ အတိုင်းအတာ၊ စံသွေဖည်မှု၊ အဓိပ္ပာယ်သွေဖည်မှုနှင့် ကွဲလွဲမှု၏ကိန်းဂဏန်းများဖြစ်သည်။

ကွာဟချက်ကို ဘယ်လိုတွက်မလဲ။

ကွဲလွဲမှုကို တွက်ချက်ရန်အတွက် အောက်ပါအဆင့်များကို လုပ်ဆောင်ရပါမည်-

ဒေတာအတွဲ၏ ဂဏန်းသင်္ချာပျမ်းမျှကို ရှာပါ။
အကြွင်းအကျန်များကို တွက်ချက်ပါ၊ တန်ဖိုးများနှင့် ဒေတာသတ်မှတ်မှု၏ ဆိုလိုရင်းအကြား ကွာခြားချက်အဖြစ် သတ်မှတ်သည်။
အကြွင်းတစ်ခုစီ လေးထောင့်။
ယခင်အဆင့်တွင် တွက်ချက်ထားသော ရလဒ်အားလုံးကို ထည့်ပါ။
အချက်အလက် စုစုပေါင်း အရေအတွက်ဖြင့် ပိုင်းပါ။ ရရှိသောရလဒ်မှာ ဒေတာစီးရီး၏ ကွဲလွဲမှုဖြစ်သည်။

နိဂုံးချုပ်အနေဖြင့်၊ ဒေတာအတွဲတစ်ခု၏ ကွဲလွဲမှုကို တွက်ချက်ရန်အတွက် ဖော်မြူလာ မှာ-

ရွှေ-

$X$

ကွဲလွဲမှုကို သင်တွက်ချက်လိုသော ကျပန်းကိန်းရှင်ဖြစ်သည်။
$x_i$

ဒေတာတန်ဖိုး

$i$

.
$n$

လေ့လာချက် စုစုပေါင်း အရေအတွက် ဖြစ်ပါသည်။
$\overline{X}$

Random variable ၏ ဆိုလိုရင်းဖြစ်ပါသည်။

$X$

.

👉 မည်သည့်ဒေတာအတွဲ၏ ကွဲလွဲမှုကို တွက်ချက်ရန် အောက်ပါ ဂဏန်းပေါင်းစက်ကို အသုံးပြုနိုင်သည်။

ထို့ကြောင့်၊ ဒေတာစီးရီးတစ်ခုမှ ကွဲလွဲမှုကို ထုတ်ယူရန်၊ ဂဏန်းသင်္ချာဆိုလိုအား တွက်ချက်ပုံကို သိထားရန် လိုအပ်ပါသည်။ ဒီလိုလုပ်နည်းကို မမှတ်မိရင် အပေါ်က link ပါတဲ့ ဆောင်းပါးမှာ ကြည့်ပါ။

သွေဖည်ခြင်းဥပမာ

ကွဲလွဲမှု၏အဓိပ္ပါယ်ကို ယခုကျွန်ုပ်တို့သိပြီးသောအခါ၊ ဒေတာစီးရီးတစ်ခု၏ကွဲလွဲမှုကိုမည်ကဲ့သို့ရရှိသည်ကိုသင်မြင်နိုင်စေရန်အတွက် လေ့ကျင့်ခန်းတစ်ဆင့်ပြီးတစ်ဆင့်ဖြေရှင်းပါမည်။

နိုင်ငံစုံကုမ္ပဏီတစ်ခုမှ လွန်ခဲ့သည့်ငါးနှစ်အတွင်း ရရှိခဲ့သော စီးပွားရေးရလဒ်ကို သိရှိကြပြီး အများစုမှာ အမြတ်အစွန်းများရရှိသော်လည်း တစ်နှစ်လျှင် ယူရို ၁၁.၅၊ ၂၊ -၉၊ ၇ သန်းအထိ အများအပြား ဆုံးရှုံးခဲ့သည်။ ဤဒေတာအတွဲ၏ ကွဲလွဲမှုကို တွက်ချက်ပါ။

အထက်ဖော်ပြပါ ရှင်းလင်းချက်တွင် ကျွန်ုပ်တို့တွေ့မြင်ရသည့်အတိုင်း၊ ဒေတာစီးရီးတစ်ခု၏ ကွဲလွဲမှုကို ရှာဖွေရန် ပထမဆုံးလုပ်ဆောင်ရမည့်အရာမှာ ၎င်း၏ဂဏန်းသင်္ချာဆိုလိုအား တွက်ချက်ရန်ဖြစ်သည်-

$\overline{X}=\cfrac{11+5+2+(-9)+7}{5}=3,2$

ဒေတာ၏ ပျမ်းမျှတန်ဖိုးကို သိသည်နှင့်၊ ကွဲပြားမှု ဖော်မြူလာကို အသုံးပြုနိုင်သည်။

$Var(X)=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2}{n}$

ကျွန်ုပ်တို့သည် လေ့ကျင့်ခန်းထုတ်ပြန်ချက်မှ ပံ့ပိုးပေးထားသော အချက်အလက်များကို ဖော်မြူလာအဖြစ် အစားထိုးသည်-

$Var(X)=\cfrac{\displaystyle (11-3,2)^2+(5-3,2)^2+(2-3,2)^2+(-9-3,2)^2+(7-3,2)^2}{5}$

နောက်ဆုံးတွင်၊ ကွဲလွဲမှုကို တွက်ချက်ရန် လုပ်ဆောင်ချက်များကို ဖြေရှင်းရန် ကျန်ရှိနေသေးသည်-

$\begin{aligned}Var(X)&=\cfrac{7,8^2+1,8^2+(-1,2)^2+(-12,2)^2+3,8^2}{5}\\[2ex]&=\cfrac{60,84+3,24+1,44+148,84+14,44}{5}\\[2ex]&= \cfrac{228,8}{5} \\[2ex]&=45,76 \ \text{millones de euros}^2\end{aligned}$

ကွဲလွဲမှုယူနစ်များသည် ကိန်းဂဏန်းအချက်အလက်များ၏တူညီသောယူနစ်များဖြစ်သော်လည်း နှစ်ထပ်ကိန်းဖြစ်ကြောင်း သတိပြုပါ၊ ထို့ကြောင့် ဤဒေတာအုပ်စု၏ကွဲလွဲမှုသည် ယူရို 45.76 သန်း ² ဖြစ်သည်။

ကွာဟချက်ဂဏန်းတွက်စက်

၎င်း၏ကွဲလွဲမှုကို တွက်ချက်ရန် အောက်ပါဂဏန်းပေါင်းစက်ထဲသို့ ကိန်းဂဏန်းအချက်အလက်ကို ထည့်သွင်းပါ။ ဒေတာကို နေရာလွတ်တစ်ခုဖြင့် ပိုင်းခြားထားရမည်ဖြစ်ပြီး ဒဿမပိုင်းခြားခြင်းအဖြစ် ကာလကို အသုံးပြု၍ ထည့်သွင်းရပါမည်။

အုပ်စုဖွဲ့ဒေတာအတွက် ကွဲလွဲမှု

ကြားကာလများအဖြစ် အုပ်စုဖွဲ့ထားသော ဒေတာကွဲလွဲမှုကို တွက်ချက်ရန် ၊ အောက်ပါအဆင့်များကို လိုက်နာရပါမည်-

အုပ်စုဖွဲ့ဒေတာ၏ ဆိုလိုရင်းကို ရှာပါ။
အုပ်စုဖွဲ့ထားသောဒေတာ၏ ကျန်ရှိသောများကို တွက်ချက်ပါ။
အကြွင်းတစ်ခုစီ လေးထောင့်။
ယခင်ရလဒ်တစ်ခုစီကို ၎င်း၏ကြားကာလ၏ကြိမ်နှုန်းဖြင့် မြှောက်ပါ။
ယခင်အဆင့်တွင်ရရှိသောတန်ဖိုးများအားလုံး၏ပေါင်းလဒ်ကိုထည့်ပါ။
စုစုပေါင်း လေ့လာတွေ့ရှိချက်အရေအတွက်ဖြင့် ပိုင်းခြားပါ။ ရလဒ်နံပါတ်သည် အုပ်စုဖွဲ့ထားသောဒေတာ၏ ကွဲလွဲမှုဖြစ်သည်။

တစ်နည်းအားဖြင့်၊ ကြားကာလများအဖြစ် အုပ်စုဖွဲ့ထားသော ဒေတာကွဲလွဲမှုကို တွက်ချက်ရန်အတွက် ဖော်မြူလာမှာ အောက်ပါအတိုင်းဖြစ်သည်။

$Var(X)=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2\cdot f_i }{n}$

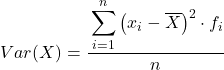
အထက်ဖော်ပြပါ ဖော်မြူလာကို ပုံမှန်အားဖြင့် အသုံးပြုသော်လည်း၊ အောက်ဖော်ပြပါ အက္ခရာသင်္ချာအညွှန်းကိန်းကို ၎င်းနှင့် ညီမျှသောကြောင့် အသုံးပြုနိုင်သည်။

$Var(X)=\cfrac{\displaystyle\sum_{i=1}^n x_i^2\cdot f_i }{n}-\overline{X}^2$

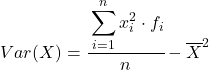
ဥပမာအနေဖြင့်၊ အောက်ပါအုပ်စုဖွဲ့ထားသော ဒေတာစီးရီး၏ ကွဲလွဲမှုကို ကျွန်ုပ်တို့ တွေ့ရပါမည်-

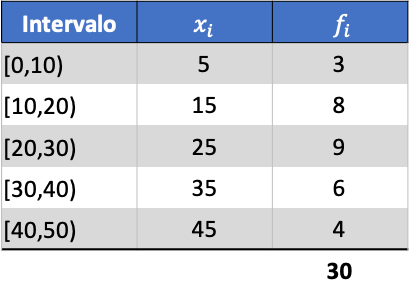
ဒေတာများကို ကြားကာလအဖြစ် အုပ်စုဖွဲ့ထားသည်။

ပထမဦးစွာ ကျွန်ုပ်တို့သည် အုပ်စုဖွဲ့ထားသောဒေတာ၏ ပျမ်းမျှအား ဆုံးဖြတ်ရန် လိုအပ်သည်။ ဒါကိုလုပ်ဖို့၊ အတန်းအမှတ်အသားရဲ့ ထုတ်ကုန်နဲ့ ကြိမ်နှုန်းနဲ့ ကြိမ်နှုန်းဇယားထဲမှာ ကော်လံတစ်ခုကို ပေါင်းထည့်ပါ

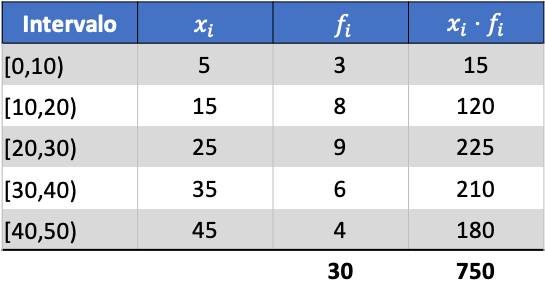
ယခု ကျွန်ုပ်တို့သည် ထပ်လောင်းကော်လံ၏ပေါင်းလဒ်ကို ဒေတာစုစုပေါင်းအရေအတွက်ဖြင့် ပိုင်းခြားခြင်းဖြင့် အုပ်စုဖွဲ့ထားသောဒေတာ၏ပျမ်းမျှအား တွက်ချက်သည်-

$\overline{X}=\cfrac{\displaystyle\sum_{i=1}^n x_i\cdot f_i}{n}=\cfrac{750}{30}=25$

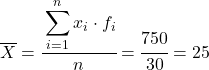
တွက်ချက်ထားသော ဒေတာ၏ ပျမ်းမျှအားဖြင့်၊ ကျွန်ုပ်တို့သည် အောက်ပါကော်လံသုံးခုကို ထည့်နိုင်သည်။

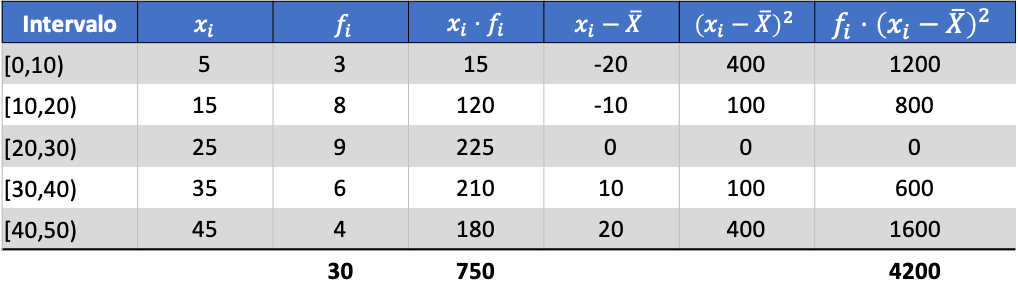
ထို့ကြောင့် စုပေါင်းထားသော ဒေတာအတွဲ၏ ကွဲလွဲမှုသည် စောင့်ကြည့်လေ့လာထားသော အချက်အလက် စုစုပေါင်းအရေအတွက်ဖြင့် ပိုင်းခြားထားသော နောက်ဆုံးကော်လံ၏ ပေါင်းလဒ်ဖြစ်သည်-

$Var(X)=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2\cdot f_i }{n}=\cfrac{4200}{30}=140$

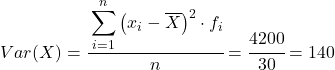
ကွဲလွဲမှုနှင့် စံသွေဖည်မှု

ကွဲလွဲမှု နှင့် စံသွေဖည်မှု (သို့မဟုတ် စံသွေဖည်မှု) သည် ကွဲလွဲမှု၏ အတိုင်းအတာ နှစ်ခုဖြစ်ပြီး ထို့ကြောင့် နှစ်ခုလုံးသည် ဒေတာအစု၏ ကွဲလွဲမှုအတိုင်းအတာကို ညွှန်ပြပါသည်။ သို့ရာတွင်၊ ကွဲလွဲမှုနှင့် စံသွေဖည်မှုကြား ခြားနားချက် မှာ ယေဘုယျကွဲလွဲမှုတွင် စံသွေဖည်မှု၏ နှစ်ထပ်ဖြစ်သောကြောင့် ယေဘုယျအားဖြင့် ကွဲလွဲမှုတန်ဖိုးများ ပိုကြီးပါသည်။

စံသွေဖည်မှုကို ယေဘူယျအားဖြင့် ဂရိအက္ခရာ sigma (σ) ဖြင့် ကိုယ်စားပြုပြီး ယင်းကြောင့် ကွဲလွဲမှုကို အက္ခရာ sigma နှစ်ထပ်ကိန်း (σ ² ) ဖြင့် ကိုယ်စားပြုထားသောကြောင့် ၎င်းသည် ဤပြန့်ကျဲနေသော မက်ထရစ်နှစ်ခုကြားရှိ သင်္ချာဆိုင်ရာ ဆက်နွယ်မှုဖြစ်သောကြောင့် ဖြစ်သည်။

$Var(X)=\sigma^2$

ထို့ကြောင့်၊ သင်သည် ဒေတာအစုတစ်ခု၏ ကွဲလွဲမှုတန်ဖိုးကို တွက်ချက်ပြီးသည်နှင့်၊ ကွဲလွဲမှု၏ နှစ်ထပ်ကိန်းကို ရိုးရိုးရှင်းရှင်းယူရုံဖြင့် ထိုအစု၏ စံသွေဖည်တန်ဖိုးကို အလွယ်တကူ ရှာဖွေနိုင်သည်။

$\sigma=\sqrt{\sigma^2}$

လူဦးရေကွဲလွဲမှုနှင့် နမူနာကွဲလွဲမှု

ယုတ္တိနည်းအားဖြင့်၊ လူဦးရေကွဲလွဲမှုသည် စာရင်းအင်းလူဦးရေ၏ကွဲလွဲမှုကို တွက်ချက်ခြင်းကို ရည်ညွှန်းပြီး ယင်းအစား နမူနာကွဲလွဲမှုကို နမူနာတစ်ခု၏ကွဲလွဲမှုတွက်ချက်မှုတွင် အသုံးချသည်။ သို့သော်၊ လူဦးရေကွဲလွဲမှုဖော်မြူလာသည် နမူနာကွဲလွဲမှုဖော်မြူလာနှင့် ကွဲပြားသောကြောင့် ၎င်းတို့သည် မတူညီသော အယူအဆနှစ်ခုဖြစ်သည်။

ပုံမှန်အားဖြင့် မတူညီသော လေ့ကျင့်ခန်းများတွင် ၎င်းတို့က ကျွန်ုပ်တို့အား ပေးထားသော ဒေတာအတွဲ၏ ကွဲလွဲမှုကို ရှာဖွေရန် ဆောင်းပါးအစမှ ရှင်းပြထားသည့် လူဦးရေကွဲလွဲမှု ဖော်မြူလာကို အသုံးပြုရပါမည်၊

$\sigma^2=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2}{n}$

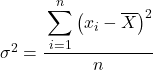
သို့သော် အချို့သောပြဿနာများတွင် ကိန်းဂဏန်းအချက်အလက်များကို နမူနာအဖြစ် ဆက်ဆံရန် သင့်အား တောင်းဆိုခံရကောင်းဖြစ်နိုင်သည်၊ ယင်းအခြေအနေတွင် ကျွန်ုပ်တို့သည် နမူနာကွဲလွဲမှုဖော်မြူလာကို အသုံးပြုရန်လိုအပ်ပါသည်။

$s^2=\cfrac{\displaystyle\sum_{i=1}^n\left(x_i-\overline{X}\right)^2}{n-1}$

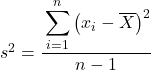
လူဦးရေကွဲလွဲမှုကို တွက်ချက်နေကြောင်း ညွှန်ပြရန် ၎င်းကို ဂရိအက္ခရာ σ ဖြင့် ညွှန်ပြသော်လည်း နမူနာကွဲလွဲမှုကို တွက်ချက်သောအခါတွင် စာလုံး s ကို အသုံးပြုသည်။

သင်တွေ့မြင်ရသည့်အတိုင်း၊ ဖော်မြူလာနှစ်ခုကြားတွင် တစ်ခုတည်းသော ကွာခြားချက်မှာ နမူနာတစ်ခု၏ ကွဲလွဲမှုတွင် ကျွန်ုပ်တို့သည် စုစုပေါင်းလေ့လာချက်အရေအတွက် အနှုတ် 1 ဖြင့် ပိုင်းခြားရန် လိုအပ်သည်၊ ဥပမာ၊ ဒေတာစုစုပေါင်း 30 ရှိလျှင် 29 ဖြင့် ခွဲမည်၊ သို့သော် ပိုင်းဝေတွက်ချက်မှုကို အတိအကျတူညီသောနည်းဖြင့် လုပ်ဆောင်သည်။

ကွဲလွဲမှု သတ္တိ

ကွဲလွဲမှုတွင် အောက်ပါဂုဏ်သတ္တိများရှိသည်။

မည်သည့်ကျပန်းကိန်းရှင်၏ကွဲလွဲမှုသည် သုညထက် ကြီးသည် သို့မဟုတ် ညီမျှနေမည်ဖြစ်သည်။ အလားတူ၊ ကွဲလွဲမှု သုညဖြစ်ပါက၊ ကိန်းဂဏန်းအချက်အလက်အားလုံးသည် တူညီသည်ဟု ဆိုလိုသည်။

$Var(x)\ge 0$

တန်ဖိုးတစ်ခု၏ကွဲလွဲမှုသည် သုညဖြစ်သည်မှာ ထင်ရှားသည်။

$Var(a)=0\qquad a\in \mathbb{R}$

ကိန်းရှင်တစ်ခုဖြင့် စကေးတစ်ခု၏ ရလဒ်၏ကွဲလွဲမှုသည် ထိုကိန်းရှင်၏ကွဲလွဲမှု၏ကွဲလွဲမှု၏နှစ်ထပ်ကိန်းနှင့် အမြှောက်နှင့် ညီမျှသည်။

$Var(aX)=a^2\cdot Var(X)\qquad a\in \mathbb{R}$

မှီခိုကိန်းရှင်နှစ်ခု၏ ပေါင်းလဒ်ကွဲလွဲမှုသည် ကိန်းရှင်တစ်ခုစီ၏ကွဲလွဲမှု၏ပေါင်းလဒ်နှင့် ညီမျှပြီး ကိန်းရှင်နှစ်ခုကြားရှိ ကွဲလွဲမှုနှစ်ဆကို ခွဲခြားထားသည်။

$Var(X+Y)=Var(X)+Var(Y)+2Cov(X,Y)$

ထို့ကြောင့်၊ ကိန်းရှင်နှစ်ခုသည် အမှီအခိုကင်းပါက၊ ၎င်းတို့၏ ပေါင်းလဒ်ကွဲလွဲမှုကို ဆုံးဖြတ်ရန် ၎င်းတို့၏ကွဲလွဲမှုများကို ထည့်ရန် လုံလောက်သည်-

$Var(X+Y)=Var(X)+Var(Y)$

သွေဖည်မှုကို အောက်ပါဖော်မြူလာကို အသုံးပြု၍ သင်္ချာမျှော်လင့်ချက်ဖြင့်လည်း သတ်မှတ်နိုင်သည်-

$Var(X)=E\bigl[(X-\overline{X})^2\bigr]$

စာရေးသူအကြောင်း

Benjamin Anderson

မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။