ကွဲလွဲမှု

အားဖြင့် Benjamin Anderson ဩဂုတ် 5, 2023 စာရင်းအင်းများ 0 မှတ်ချက်များ

ဤဆောင်းပါးတွင် ကွဲလွဲမှုဆိုသည်မှာ မည်ကဲ့သို့ တွက်ချက်သည်ကို ရှင်းပြထားသည်။ ကွဲလွဲမှုဖော်မြူလာအပြင် ဒေတာအစုတစ်ခု၏ ကွဲလွဲမှုကို တွက်ချက်ခြင်း၏ ဥပမာတစ်ခုကို သင်တွေ့လိမ့်မည်။ ထို့အပြင်၊ အဆုံးတွင် အွန်လိုင်းဂဏန်းတွက်စက်ဖြင့် မည်သည့်ဒေတာစီးရီးများ၏ ကွဲလွဲမှုကို တွက်ချက်နိုင်သည်။

ကွဲလွဲမှုဆိုတာဘာလဲ။

စာရင်းဇယားများတွင်၊ ကွဲလွဲမှုသည် ကျပန်းကိန်းရှင်နှစ်ခု၏ ပူးတွဲကွဲလွဲမှုအဆင့်ကို ညွှန်ပြသည့် တန်ဖိုးတစ်ခုဖြစ်သည်။ တစ်နည်းအားဖြင့် ကိန်းရှင်နှစ်ခုကြား မှီခိုမှုကို ပိုင်းခြားစိတ်ဖြာရန် ကွဲလွဲမှုကို အသုံးပြုသည်။

ကွဲလွဲချက်နှစ်ခုသည် ကိန်းရှင်နှစ်ခု၏ ဒေတာအကြား ကွာခြားချက်များ၏ ထုတ်ကုန်များ၏ ပေါင်းလဒ်နှင့် ညီမျှပြီး ၎င်းတို့၏ သက်ဆိုင်ရာ ဒေတာစုစုပေါင်း အရေအတွက်ဖြင့် ပိုင်းခြားထားသော နည်းလမ်းများဖြစ်သည်။

👉 မည်သည့်ဒေတာအတွဲ၏ ကွဲလွဲမှုကို တွက်ချက်ရန် အောက်ပါ ဂဏန်းပေါင်းစက်ကို အသုံးပြုနိုင်သည်။

ကွဲလွဲမှုတန်ဖိုး၏ အဓိပ္ပာယ်ဖွင့်ဆိုချက်သည် အလွန်ရိုးရှင်းပါသည်။

ကွဲလွဲမှုမှာ အပြုသဘောဆောင် ပါက၊ ကိန်းရှင်နှစ်ခုကြားတွင် မှီခိုမှုရှိကြောင်း ဆိုလိုသည်။ ထို့ကြောင့် variable တစ်ခုသည် တန်ဖိုးတက်လာသောအခါ၊ အခြားသော variable သည်လည်း တိုးလာပြီး အပြန်အလှန်အားဖြင့် တိုးလာပါသည်။
ကွဲလွဲမှုမှာ အနှုတ် ဖြစ်ပါက၊ ကိန်းရှင်နှစ်ခုကြားရှိ ဆက်နွယ်မှုသည် အနုတ်လက္ခဏာဖြစ်သည်။ ထို့ကြောင့် variable တစ်ခုသည် တန်ဖိုးတက်လာသောအခါ၊ အခြား variable သည် လျော့နည်းသွားပြီး အပြန်အလှန်အားဖြင့်၊
ကွဲလွဲမှုသည် သုည (သို့မဟုတ် ၎င်း၏တန်ဖိုးသည် သုညနှင့်နီးစပ်သည်)၊ ၎င်းသည် ကိန်းရှင်နှစ်ခုကြားတွင် ဆက်စပ်မှုမရှိဟု ဆိုလိုသည်။ တစ်နည်းဆိုရသော် ကျပန်းကိန်းရှင်နှစ်ခုသည် သီးခြားဖြစ်သည်။

ကွဲလွဲမှုကို တွက်ချက်နည်း

ဒေတာစီးရီးတစ်ခု၏ ကွဲလွဲမှုကို တွက်ချက်ရန်၊ အောက်ပါအဆင့်များကို လုပ်ဆောင်ရပါမည်-

ကိန်းရှင်တစ်ခုစီ၏ ပျမ်းမျှအား သီးခြားစီ တွက်ချက်ပါ။
ကိန်းရှင်တစ်ခုစီအတွက်၊ ၎င်း၏တန်ဖိုးတစ်ခုစီနှင့် ကိန်းရှင်၏ပျမ်းမျှအကြား ခြားနားချက်ကို ရှာပါ။
ဒေတာအမှတ်တစ်ခုစီအတွက် ယခင်အဆင့်တွင် တွက်ချက်ထားသော မတူညီမှုများကို မြှောက်ပါ။
ယခင်အဆင့်တွင်ရရှိသောရလဒ်အားလုံးကို ပေါင်းထည့်ပါ။
အချက်အလက် စုစုပေါင်း အရေအတွက်ဖြင့် ပိုင်းပါ။ ရရှိသောတန်ဖိုးသည် ဒေတာစီးရီး၏ ကွဲလွဲမှုဖြစ်သည်။

အချုပ်အားဖြင့်၊ ကိန်းရှင်နှစ်ခုကြားရှိ ကွဲလွဲမှုကို တွက်ချက်ရန် ဖော်မြူလာမှာ အောက်ပါအတိုင်းဖြစ်သည်။

$Cov(X,Y)=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{n}$

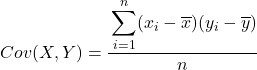
ကိန်းရှင်နှစ်ခုကြား ကွဲလွဲမှုကို ထုတ်ယူရန် အထူးအကြံပြုထားသည့်နည်းလမ်းမှာ ဒေတာအတွဲများပါရှိသော ဇယားတစ်ခုကို ဖန်တီးရန်နှင့် အထက်တွင်ဖော်ပြထားသည့် အဆင့်တစ်ဆင့်ချင်းစီအတွက် ကော်လံတစ်ခုကို ပေါင်းထည့်ခြင်းဖြစ်သည်။ ဒီလိုနည်းနဲ့ မင်းရဲ့ တွက်ချက်မှုတွေက အများကြီး ပိုကောင်းလာမှာဖြစ်ပြီး မင်းဘာလုပ်နေလဲဆိုတာကို ပိုနားလည်လာလိမ့်မယ်။

ကွဲလွဲမှု တွက်ချက်မှု ဥပမာ

ကွဲလွဲမှု၏ အဓိပ္ပါယ်ဖွင့်ဆိုချက်ကို ထည့်သွင်းစဉ်းစားခြင်းဖြင့်၊ အောက်တွင် ဤကိန်းဂဏန်းတိုင်းတာမှုအမျိုးအစားကို တွက်ချက်ခြင်း၏ အဆင့်ဆင့် ဥပမာတစ်ခုဖြစ်သည်။ ရည်ရွယ်ချက်မှာ ကွဲလွဲမှု၏ သဘောတရားကို ပိုမိုကောင်းမွန်စွာ နားလည်ရန်နှင့် ကိန်းရှင်နှစ်ခုကြားရှိ ဆက်စပ်မှုကို ခွဲခြမ်းစိတ်ဖြာနည်း။

အောက်ပါစာရင်းအင်းဒေတာအတွဲ၏ ကွဲလွဲမှုကို တွက်ချက်ပါ-

ဦးစွာ၊ ကိန်းရှင်တစ်ခုစီ၏ ဂဏန်းသင်္ချာပျမ်းမျှတွက်ရန် လိုအပ်သည်။ ဒါကိုလုပ်ဖို့၊ ကိန်းရှင်တစ်ခုစီရဲ့တန်ဖိုးတွေကို ဒေတာစုစုပေါင်းအရေအတွက်နဲ့ ခွဲပါတယ်။

$\overline{x}=\cfrac{58}{10}=5,8$

$\overline{y}=\cfrac{51}{10}=5,1$

➤ ဂဏန်းသင်္ချာပုံသေနည်း ဆိုလိုချက်ကို ကြည့်ပါ ။

ကျွန်ုပ်တို့သည် ကျပန်းပြောင်းလဲနိုင်သောကိန်းရှင်တစ်ခုစီ၏ ဆိုလိုရင်းကို ဆုံးဖြတ်ပြီးသည်နှင့်၊

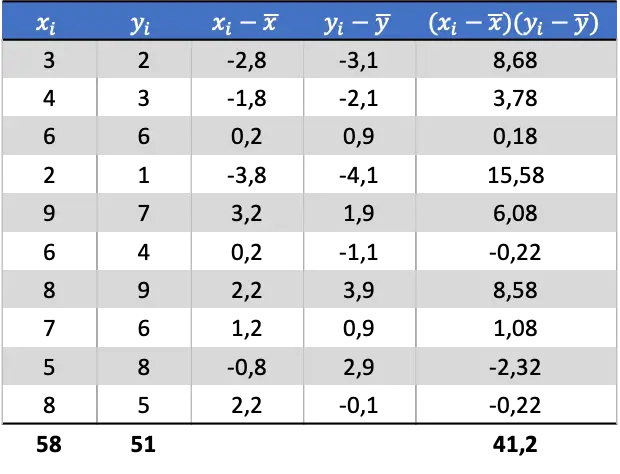
sibiance လေ့ကျင့်ခန်းကို ဖြေရှင်းနိုင်ပါတယ်။

ထို့ကြောင့် ကိန်းရှင်နှစ်ခု၏ ကွဲလွဲမှုကို ဆုံးဖြတ်ရန် နောက်ဆုံးကော်လံ၏ ပေါင်းလဒ်ကို ဒေတာအတွဲအရေအတွက်ဖြင့် ပိုင်းခြားရပါမည်။

$\begin{aligned}Cov(X,Y)&=\cfrac{\displaystyle \sum_{i=1}^n (x_i-\overline{x})(y_i-\overline{y})}{n}\\[2ex] Cov(X,Y)&= \cfrac{41,2}{10} \\[2ex]Cov(X,Y)&= 4,12\end{aligned}$

ဤအခြေအနေတွင် ကွဲလွဲမှုတန်ဖိုးသည် အပြုသဘောဆောင်သည်၊ ဆိုလိုသည်မှာ လေ့လာထားသော ကျပန်းကိန်းရှင်နှစ်ခုကြားတွင် တိုက်ရိုက်မှီခိုမှုရှိကြောင်း ဆိုလိုသည်။ သို့ရာတွင်၊ ကွဲလွဲမှုတန်ဖိုးသည် အနုတ်လက္ခဏာဖြစ်လျှင်၊ ၎င်းသည် ကိန်းရှင်နှစ်ခုကြားတွင် မှီခိုမှုမှာ ပြောင်းပြန်ဖြစ်သည်ဟု ဆိုလိုသည်။ နောက်ဆုံးတွင်၊ ကွဲလွဲမှုတန်ဖိုးသည် သုည သို့မဟုတ် သုညနှင့် အလွန်နီးစပ်ပါက၊ ကိန်းရှင်နှစ်ခုကြားတွင် မျဉ်းကြောင်းဆက်နွယ်မှု မရှိဟု ဆိုလိုသည်။

ဤဥပမာကိုဖြေရှင်းခြင်းမှ သင်တွေ့မြင်ရသည့်အတိုင်း၊ Excel ကဲ့သို့သော ကွန်ပျူတာပရိုဂရမ်များကို ဇယားတွင်ကော်လံများထည့်ကာ တွက်ချက်မှုများကို လျင်မြန်စွာလုပ်ဆောင်ရန် အလွန်အသုံးဝင်ပါသည်။ မဟုတ်ပါက လုပ်ဆောင်ချက်များကို ကိုယ်တိုင် တွက်ချက်ခြင်းဖြင့် ကွဲလွဲမှုကို ရှာဖွေရန် များစွာကြာပါသည်။

ကွဲလွဲမှုဂဏန်းတွက်စက်

ကိန်းရှင်နှစ်ခုကြားရှိ ကွဲလွဲမှုကို တွက်ချက်ရန် အောက်ပါဂဏန်းပေါင်းစက်ထဲသို့ ကိန်းဂဏန်းအချက်အလက်အစုတစ်စုကို ထည့်သွင်းပါ။ ဒေတာအတွဲများကို ခွဲခြားထားရန် လိုအပ်သည်၊ ထို့ကြောင့် ပထမအကွက်တွင် ကိန်းရှင်တစ်ခု၏ တန်ဖိုးများသာ ရှိပြီး ဒုတိယအကွက်တွင် ဒုတိယကိန်းရှင်၏ တန်ဖိုးများသာ ရှိနေမည်ဖြစ်သည်။

ဒေတာကို နေရာလွတ်တစ်ခုဖြင့် ပိုင်းခြားထားရမည်ဖြစ်ပြီး ဒဿမပိုင်းခြားခြင်းအဖြစ် ကာလကို အသုံးပြု၍ ထည့်သွင်းရပါမည်။

ကွဲလွဲမှု ဂုဏ်သတ္တိများ

ကွဲလွဲမှုတွင် အောက်ပါဂုဏ်သတ္တိများရှိသည်။

ကျပန်းကိန်းရှင်နှင့် ကိန်းသေတစ်ခုကြား ကွဲလွဲမှုသည် သုညဖြစ်သည်။

$Cov(X,a)=0$

ကိန်းရှင်တစ်ခု၏ ကွဲလွဲမှုဖြစ်ပြီး ၎င်းကိုယ်တိုင်သည် ထိုကိန်းရှင်၏ကွဲလွဲချက်နှင့် ညီမျှသည်။

$Cov(X,X)=Var(X)$

➤ ကွဲလွဲမှုဆိုသည်မှာ အဘယ်နည်း ။

ကွဲလွဲချက်သည် အချိုးညီသော ပိုင်ဆိုင်မှုကို ကျေနပ်စေသည်၊ ထို့ကြောင့် ကိန်းရှင် X နှင့် Y တို့၏ ကွဲလွဲမှုသည် ကိန်းရှင် Y နှင့် X တို့၏ ကွဲလွဲချက်နှင့် ညီမျှသည်။ ကိန်းရှင်များ၏ အစီအစဥ်သည် ကွဲလွဲမှု၏ ရလဒ်အပေါ် သက်ရောက်မှုမရှိပါ။

$Cov(X,Y)=Cov(Y,X)$

ကိန်းရှင်များကို ကိန်းသေများဖြင့် မြှောက်ပါက၊ သင်သည် ပထမဦးစွာ ကွာဟချက်ကို တွက်ချက်ပြီးနောက် ရလဒ်ကို ကိန်းသေများဖြင့် မြှောက်နိုင်သည်။

$Cov(a\cdot X,b\cdot Y)=a\cdot b\cdot Cov(X,Y)$

ကိန်းရှင်များသို့ ဝေါဟာရများထည့်ခြင်းသည် ကွဲလွဲမှုရလဒ်အပေါ် သက်ရောက်မှုမရှိပါ။

$Cov(a+X,b+Y)=Cov(X+Y)$

ကျပန်း variable နှစ်ခုကြား ကွဲလွဲမှုသည် ၎င်းတို့၏ သင်္ချာဆိုင်ရာ မျှော်လင့်ချက်များနှင့် ဆက်စပ်နေသည်။ ကိန်းရှင် X နှင့် Y အကြား ကွာဟချက်သည် ကိန်းရှင်တစ်ခုစီ၏ သင်္ချာမျှော်လင့်ချက်၏ ရလဒ်ဖြစ်သော X နှင့် Y ၏ အနုတ်လက္ခဏာတို့၏ သင်္ချာမျှော်မှန်းချက်နှင့် ညီမျှသည်။

$Cov(X,Y)=E[X\cdot Y]-E[X]\cdot E[Y]$

ကိန်းရှင်များနှင့် လည်ပတ်သောအခါ၊ အောက်ပါ အက္ခရာသင်္ချာအသုံးအနှုန်းသည် ကွဲလွဲမှုကို လေးစားမှုဖြင့် ပြည့်စုံသည်-

$\begin{aligned}\displaystyle Cov(aX+bY,cW+dV)= \ & \displaystyle acCov(X,W)+adCov(X,V)+\\[2ex]& +bcCov(Y,W)+bdCov(Y,V)\end{aligned}$

စာရေးသူအကြောင်း

Benjamin Anderson

မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။