Chi-square ဖြန့်ချီရေး

အားဖြင့် Benjamin Anderson ဩဂုတ် 4, 2023 ဖြစ်နိုင်ခြေ 0 မှတ်ချက်များ

ဤဆောင်းပါးတွင် chi-square ဖြန့်ဖြူးမှုမှာ အဘယ်အရာနှင့် ၎င်းကိုအသုံးပြုကြောင်း ရှင်းပြထားသည်။ ထို့အပြင်၊ သင်သည် chi-square ဖြန့်ဖြူးမှုဂရပ်နှင့် ၎င်း၏ ဂုဏ်သတ္တိများကို သင်တွေ့လိမ့်မည်။

ချီစတုရန်း ဖြန့်ဖြူးမှုကား အဘယ်နည်း။

Chi-square ဖြန့်ဖြူးမှုသည် χ² သင်္ကေတဖြစ်သည့် ဖြစ်နိုင်ခြေရှိသော ဖြန့်ဖြူးမှုတစ်ခုဖြစ်သည်။ ပို၍တိကျသည်မှာ၊ Chi-square ဖြန့်ဝေမှုသည် ပုံမှန်ဖြန့်ဝေမှုနှင့်အတူ k သီးခြားကျပန်းကိန်းရှင်များ၏ နှစ်ထပ်ကိန်း၏ ပေါင်းစုဖြစ်သည်။

ထို့ကြောင့် Chi-square ဖြန့်ဖြူးမှုတွင် လွတ်လပ်မှု k ဒီဂရီရှိသည်။ ထို့ကြောင့်၊ Chi-square ဖြန့်ဖြူးမှုတွင် ၎င်းကိုကိုယ်စားပြုသည့် ပုံမှန်ဖြန့်ဝေကိန်းရှင်များ၏ နှစ်ထပ်ကိန်းပေါင်းများကဲ့သို့ လွတ်လပ်မှုဒီဂရီများစွာရှိသည်။

$\displaystyle X\sim\chi^2_k \ \color{orange}\bm{\longrightarrow}\color{black}\ \begin{array}{l}\text{Distribuci\'on chi-cuadrado}\\[2ex]\text{con k grados de libertad}\end{array}$

Chi-square ဖြန့်ဖြူးမှုကို Pearson ဖြန့်ဖြူးခြင်း ဟုလည်း ခေါ်သည်။

Chi-square ဖြန့်ဖြူးမှုသည် gamma ဖြန့်ဖြူးမှု၏ အထူးကိစ္စရပ်ဖြစ်ကြောင်း သတိပြုသင့်သည်။

ချီစတုရန်း ဖြန့်ဖြူးမှုကို ကိန်းဂဏန်းအနုအရင့်များတွင် ဥပမာအားဖြင့် ယူဆချက်စမ်းသပ်ခြင်းနှင့် ယုံကြည်မှုကြားကာလများတွင် ကျယ်ကျယ်ပြန့်ပြန့်အသုံးပြုသည်။ ဤဖြစ်နိုင်ခြေဖြန့်ဖြူးမှုအမျိုးအစား၏ အသုံးချပလီကေးရှင်းများ အောက်တွင် ကျွန်ုပ်တို့ မြင်တွေ့ရပါမည်။

Chi-square ဖြန့်ချီရေးဂရပ်

Chi-square ဖြန့်ဖြူးခြင်း၏ အဓိပ္ပါယ်ကို ကျွန်ုပ်တို့မြင်သည်နှင့်၊ ဤဖြန့်ဖြူးမှုအမျိုးအစား၏ ဥပမာများစွာကို ဂရပ်ဖစ်ဖြင့် ကိုယ်စားပြုသည်ကို တွေ့ရမည်ဖြစ်ပါသည်။ ထို့ကြောင့် အောက်တွင် chi-square ဖြန့်ဖြူးမှု၏ ဖြစ်နိုင်ခြေ ကွက်ကွက်သည် လွတ်လပ်မှု ဒီဂရီများပေါ်မူတည်၍ မည်ကဲ့သို့ ကွဲပြားသည်ကို ကြည့်ရှုနိုင်ပါသည်။

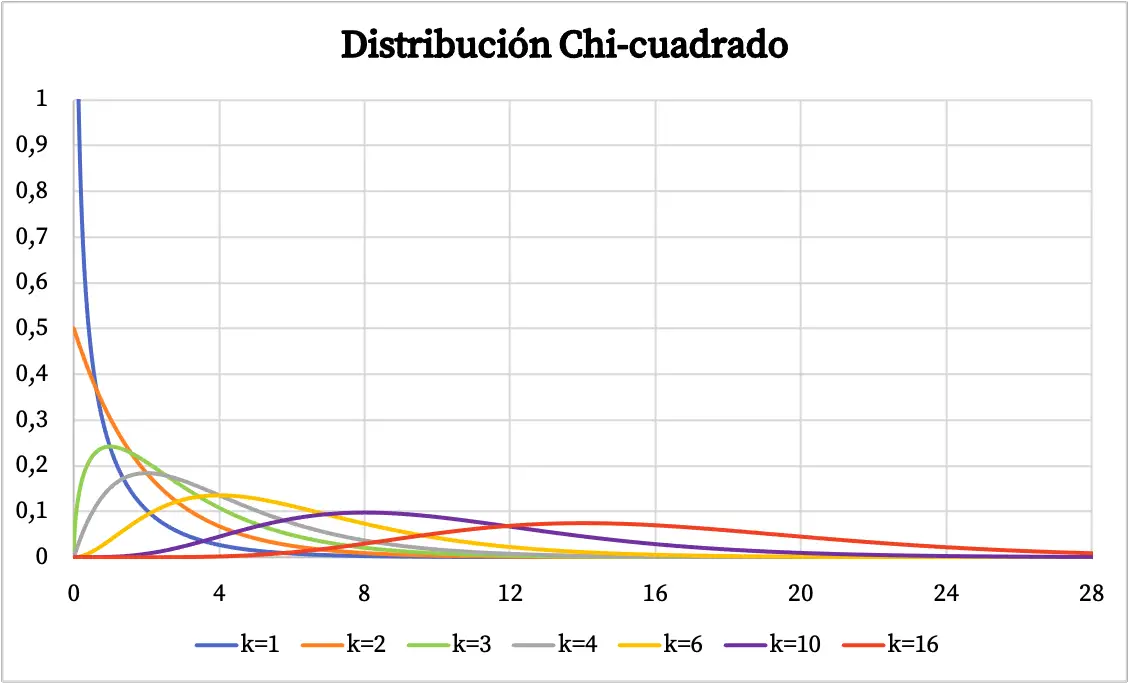
Chi-square ဖြန့်ဖြူးမှု၏ သိပ်သည်းဆလုပ်ဆောင်ချက်ကို အထက်ဖော်ပြပါ ဂရပ်တွင် ဖော်ပြထားပါသည်။ အခြားတစ်ဖက်တွင်၊ chi-square စုစည်းမှုဖြစ်နိုင်ခြေဖြန့်ဝေမှုလုပ်ဆောင်ချက်၏ဂရပ်သည် အောက်ပါအတိုင်းဖြစ်သည်-

➤ Chi-square ဖြန့်ချီရေးဇယားကို ကြည့်ပါ။

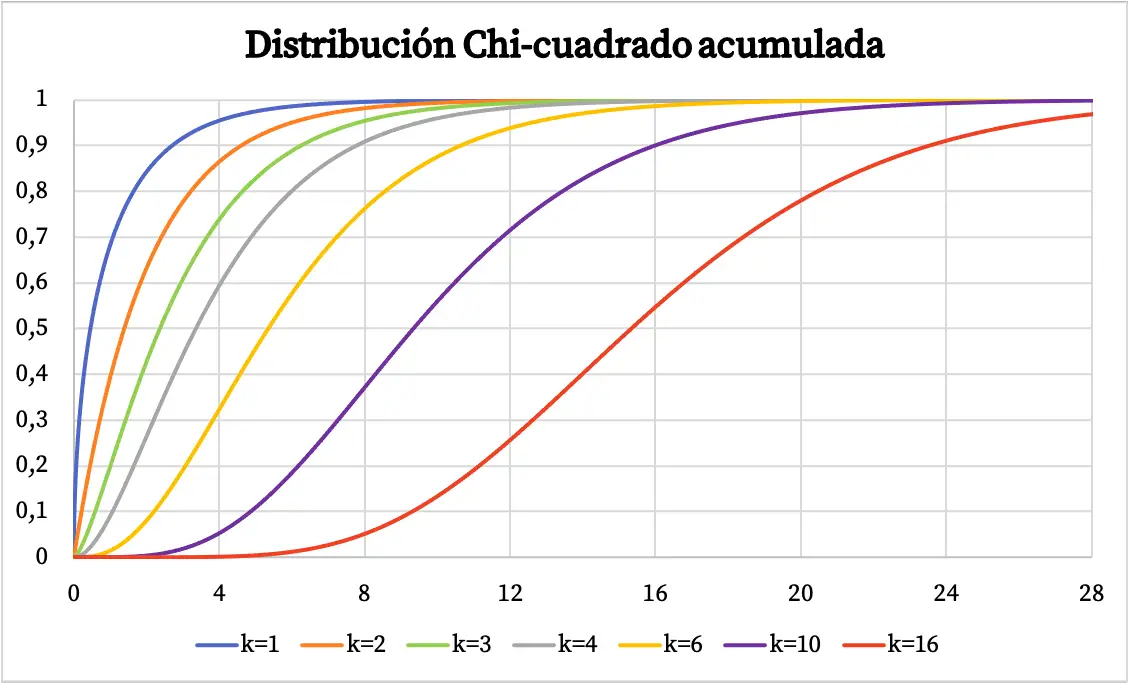
ချီစတုရန်း ဖြန့်ဖြူးခြင်း၏ လက္ခဏာများ

ဤအပိုင်းတွင် ဖြစ်နိုင်ခြေသီအိုရီနှင့် စာရင်းဇယားများနှင့်ဆက်စပ်သော Chi-square ဖြန့်ဖြူးမှု၏ အရေးကြီးဆုံးဂုဏ်သတ္တိများကို ကျွန်ုပ်တို့ မြင်တွေ့ရပါမည်။

ချီစတုရန်း ဖြန့်ဖြူးမှု၏ ပျမ်းမျှသည် ၎င်း၏ လွတ်လပ်မှု ဒီဂရီများနှင့် ညီမျှသည်။

$\begin{array}{c}X\sim\chi^2_k\\[2ex] E[X]=k\end{array}$

Chi-square ဖြန့်ဖြူးမှု၏ကွဲလွဲမှုသည် ဖြန့်ဖြူးမှု၏လွတ်လပ်မှုဒီဂရီ၏နှစ်ဆနှင့်ညီမျှသည်။

$\begin{array}{c}X\sim\chi^2_k\\[2ex] Var(X)=2\cdot k\end{array}$

ဖြန့်ဖြူးမှုတွင် လွတ်လပ်မှုအတိုင်းအတာတစ်ခုထက်ပို၍ ရှိနေသရွေ့ chi-square ဖြန့်ဖြူးမှုမုဒ်သည် ၎င်း၏လွတ်လပ်မှုဒီဂရီအောက် နှစ်ယူနစ်ဖြစ်သည်။

$Mo=k-2 \qquad \text{si } k\geq 2$

Chi-square ဖြန့်ဝေမှု၏ သိပ်သည်းဆသည် x=0 ဆိုလျှင် သုညဖြစ်သည်။ သို့ရာတွင်၊ 0 ထက်ကြီးသော x တန်ဖိုးများအတွက် Chi-square ဖြန့်ဝေမှု၏ သိပ်သည်းဆလုပ်ဆောင်ချက်ကို အောက်ပါဖော်မြူလာဖြင့် သတ်မှတ်သည်-

$\displaystyle P[X=x]= \frac{(1/2)^{k/2}}{\Gamma(k/2)} x^{k/2 - 1} e^{-x/2}$

Chi-square ဖြန့်ဝေမှု၏ စုစည်းဖြန့်ဝေမှုလုပ်ဆောင်ချက်ကို အောက်ပါဖော်မြူလာဖြင့် အုပ်ချုပ်သည်-

$\displaystyle P[X\leq x]=\frac{\gamma(k/2,x/2)}{\Gamma(k/2)}$

Chi-square ဖြန့်ဖြူးမှု၏ လွဲမှားသောကိန်းဂဏန်းသည် ဖြန့်ဖြူးမှု၏လွတ်လပ်မှုဒီဂရီအရေအတွက်ဖြင့် ပိုင်းခြားထားသော ရှစ်ခု၏လဒ်၏ နှစ်ထပ်ကိန်းဖြစ်သည်။

$\displaystyle A=\sqrt{\frac{8}{k}}$

Chi-square ဖြန့်ဖြူးမှု၏ kurtosis ကို အောက်ပါစကားရပ်ဖြင့် တွက်ချက်သည်-

$C=3+\cfrac{12}{k}$

ဗဟိုကန့်သတ်သီအိုရီကြောင့် k သည် အလုံအလောက်ကြီးပါက chi-square ဖြန့်ဝေမှုကို ပုံမှန်ဖြန့်ဖြူးခြင်းဖြင့် ခန့်မှန်းနိုင်သည်။

$\displaystyle\lim_{k \to \infty} \frac{\chi^2_k (x)}{ k } = N_{\left(1,\sqrt{2/k}\right)} (x)$

chi-square ဖြန့်ဖြူးမှုဆိုင်ရာ အသုံးချမှုများ

chi-square ဖြန့်ဖြူးမှုတွင် စာရင်းဇယားများတွင် မတူညီသော အပလီကေးရှင်းများစွာရှိသည်။ အမှန်မှာ၊ ကိန်းရှင်များအကြား လွတ်လပ်မှုနှင့် သီအိုရီခွဲဝေမှုတစ်ခုအတွက် အံဝင်ခွင်ကျဖြစ်မှုကို စစ်ဆေးရန် အသုံးပြုသည့် ချီစတုရန်းစစ်ဆေးမှုပင် ရှိပါသည်။ ဥပမာအားဖြင့်၊ နမူနာတစ်ခု၏ဒေတာသည် Poisson ဖြန့်ဖြူးမှုနှင့် ကိုက်ညီမှုရှိမရှိ ဆုံးဖြတ်ရန် Chi-square စမ်းသပ်မှုကို အသုံးပြုနိုင်သည်။

linear regression ပိုင်းခြားစိတ်ဖြာမှုတွင်၊ chi-square ဖြန့်ဖြူးမှုကို ပုံမှန်ဖြန့်ဝေနေသော လူဦးရေ၏ပျမ်းမျှအား ခန့်မှန်းရန်နှင့် linear regression study line ၏ slope ကို ခန့်မှန်းရန်အတွက်လည်း အသုံးပြုပါသည်။

နောက်ဆုံးတွင်၊ Chi square ဖြန့်ဖြူးမှုသည် Snedecor F ဖြန့်ဖြူးမှုနှင့် ၎င်း၏ဆက်နွယ်မှုမှတစ်ဆင့် ကွဲလွဲမှု၏ခွဲခြမ်းစိတ်ဖြာမှုတွင်လည်း ပါဝင်ပါသည်။

စာရေးသူအကြောင်း

Benjamin Anderson

မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။