ဂဏန်းသင်္ချာ ပျမ်းမျှ

အားဖြင့် Benjamin Anderson ဩဂုတ် 6, 2023 စာရင်းအင်းများ 0 မှတ်ချက်များ

ဤနေရာတွင် ဂဏန်းသင်္ချာဆိုသည်မှာ မည်ကဲ့သို့ တွက်ချက်သည်ကို ကျွန်ုပ်တို့ ရှင်းပြပါသည်။ မည်သည့်ကိန်းဂဏန်းနမူနာ၏ ဂဏန်းသင်္ချာဆိုလိုချက်ကို ရှာဖွေရန် ဂဏန်းသင်္ချာဥပမာများနှင့် ဂဏန်းပေါင်းစက်ကိုပင် သင်တွေ့ရပါမည်။ နောက်ဆုံးတွင်၊ ဤပျမ်းမျှအမျိုးအစား၏ ဂုဏ်သတ္တိများနှင့် ဂဏန်းသင်္ချာပျမ်းမျှအား ကြားကာလများအဖြစ် အုပ်စုဖွဲ့ထားသော ဒေတာဖြင့် မည်သို့ရယူသည်ကို သင်မြင်နိုင်မည်ဖြစ်သည်။

ဂဏန်းသင်္ချာဟူသည် အဘယ်နည်း။

ဂဏန်းသင်္ချာဆိုလိုသည် ကိန်းဂဏန်းအချက်အလက်အစုတစ်ခု၏ ဗဟိုတန်ဖိုးလက္ခဏာတစ်ခုဖြစ်သည်။ ဂဏန်းသင်္ချာပျမ်းမျှအား တွက်ချက်ရန်၊ တန်ဖိုးအားလုံးကို ဒေတာစုစုပေါင်းအရေအတွက်ဖြင့် ပေါင်းထည့်ပါသည်။

ထို့အပြင်၊ ဂဏန်းသင်္ချာပျမ်းမျှသည် နမူနာတစ်ခုအား ကိန်းဂဏန်းစာရင်းအင်းလေ့လာမှုတစ်ခုပြုလုပ်ရန် အသုံးပြုသည့် အဓိကညွှန်းကိန်းတစ်ခုဖြစ်သည်။

ထို့ကြောင့် ဂဏန်းသင်္ချာပျမ်းမျှအတွက် ဖော်မြူလာမှာ အောက်ပါအတိုင်းဖြစ်သည်။

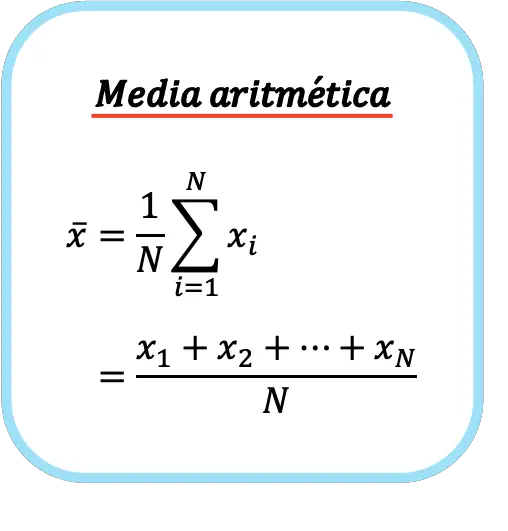
ဂဏန်းသင်္ချာအတွက် သင်္ကေတ သည် x အက္ခရာအထက် အလျားလိုက်ဝိုင်းတစ်ခုဖြစ်သည်။

$(\overline{x}).$

နမူနာဆိုလိုအား ပျမ်းမျှသင်္ကေတဖြင့် လူဦးရေဆိုလိုမှ ခွဲခြားနိုင်သည်- နမူနာတစ်ခု၏ဆိုလိုအား သင်္ကေတဖြင့် ဖော်ပြသည်

$\overline{x}$

အခြားတစ်ဖက်တွင်၊ လူဦးရေ၏ပျမ်းမျှအတွက်၊ ကျွန်ုပ်တို့သည် ဂရိအက္ခရာကိုသုံးသည်။

$\mu.$

လူဦးရေ၏ဂဏန်းသင်္ချာပျမ်းမျှသည် ကိန်းဂဏန်းကိန်းရှင်၏မျှော်မှန်းတန်ဖိုးနှင့် ညီမျှကြောင်း သတိပြုသင့်သည်။

ဂဏန်းသင်္ချာဆိုလိုသည်မှာ ဂဏန်းသင်္ချာဟုလည်း ခေါ်သည် ဆိုသည်မှာ တစ်ခုတည်းသော ကိန်းဂဏန်း အမျိုးအစား မဟုတ်ပါ၊ အလေးချိန် အတိုင်းအတာ၊ စတုရန်း ပျမ်းမျှ၊ ဂျီဩမေတြီ ပျမ်းမျှ နှင့် ဟာမိုနီဆိုလို စသည်တို့လည်း ရှိသေးသည်။ ကျွန်ုပ်တို့၏ ဝဘ်ဆိုက်၏ ရှာဖွေရေးအင်ဂျင်တွင် ၎င်းတို့တစ်ခုစီကို မည်သို့တွက်ချက်ထားသည်ကို သင်ကြည့်ရှုနိုင်သည်။

ဂဏန်းသင်္ချာ တွက်နည်း

ဂဏန်းသင်္ချာပျမ်းမျှတွက်ရန်၊ အောက်ပါအဆင့်များကို လုပ်ဆောင်ရပါမည်-

နမူနာမှ ကိန်းဂဏန်းအချက်အလက်အားလုံးကို ထည့်ပါ။
ယခင်ပေါင်းလဒ်ကို ဒေတာစုစုပေါင်းအရေအတွက်ဖြင့် ပိုင်းပေးပါ။
ရရှိသောရလဒ်မှာ ကိန်းဂဏန်းနမူနာ၏ ဂဏန်းသင်္ချာပျမ်းမျှဖြစ်သည်။

👉 မည်သည့်ဒေတာအစုံ၏ဂဏန်းသင်္ချာပျမ်းမျှတွက်ရန် အောက်ပါ ဂဏန်းပေါင်းစက်ကို အသုံးပြုနိုင်သည်။

ဂဏန်းသင်္ချာ ပျမ်းမျှတွက်နည်း ဥပမာ

ဂဏန်းသင်္ချာဆိုလိုရင်း၏ အဓိပ္ပါယ်ဖွင့်ဆိုချက်ဖြင့် ဥပမာတစ်ခုကို တစ်ဆင့်ပြီးတစ်ဆင့် ဖြေရှင်းခြင်းဖြင့် ဒေတာအစုတစ်ခု၏ ဂဏန်းသင်္ချာပျမ်းမျှကို မည်သို့ရနိုင်သည်ကို ကျွန်ုပ်တို့ မြင်တွေ့ရမည်ဖြစ်သည်။

ကျောင်းသားတစ်ဦးသည် စာသင်နှစ်တွင် အောက်ပါအဆင့်များကို အောင်မြင်ခဲ့သည်- သင်္ချာ ၉၊ ဘာသာစကား ၇၊ သမိုင်း ၆၊ ဘောဂဗေဒ ၈ နှင့် သိပ္ပံ ၇.၅။ သင့်အဆင့်အားလုံး၏ ဂဏန်းသင်္ချာပျမ်းမျှသည် အဘယ်နည်း။

ဂဏန်းသင်္ချာပျှမ်းမျှကိုရှာရန်၊ ကျွန်ုပ်တို့သည် အတန်းအားလုံးကိုပေါင်း၍ သင်တန်းရှိ ဘာသာရပ်စုစုပေါင်းအရေအတွက်အားဖြင့် 5 ဖြစ်သည့် ဂဏန်းဖြင့် ပိုင်းခြားရန် လိုအပ်ပါသည်။ ထို့ကြောင့်၊ ကျွန်ုပ်တို့သည် ဂဏန်းသင်္ချာပျမ်းမျှဖော်မြူလာကို အသုံးပြုသည်-

$\displaystyle\overline{x}=\frac{1}{N}\sum_{i=1}^N x_i=\frac{x_1+x_2+x_3+x_4+x_5}{N}$

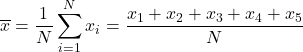
ကျွန်ုပ်တို့သည် ဒေတာကို ဖော်မြူလာအဖြစ် အစားထိုးပြီး ဂဏန်းသင်္ချာပျမ်းမျှအား တွက်ချက်သည်-

$\overline{x}=\cfrac{9+7+5+8+7,5}{5}=7,3$

သင်တွေ့မြင်ရသည့်အတိုင်း ဂဏန်းသင်္ချာပျှမ်းမျှတွင်၊ တန်ဖိုးတစ်ခုစီအတွက် တူညီသောအလေးချိန်ကို သတ်မှတ်ထားသည်၊ ဆိုလိုသည်မှာ ဒေတာအပိုင်းတစ်ခုစီတွင် အလေးချိန်တူညီပါသည်။

ဂဏန်းသင်္ချာ ပျမ်းမျှဂဏန်းတွက်စက်

၎င်း၏ဂဏန်းသင်္ချာပျမ်းမျှတွက်ရန် အောက်ဖော်ပြပါ ဂဏန်းပေါင်းစက်ထဲသို့ မည်သည့် ကိန်းဂဏန်းနမူနာမှ ဒေတာကို ထည့်သွင်းပါ။ ဒေတာကို နေရာလွတ်တစ်ခုဖြင့် ပိုင်းခြားထားရမည်ဖြစ်ပြီး ဒဿမပိုင်းခြားခြင်းအဖြစ် ကာလကို အသုံးပြု၍ ထည့်သွင်းရပါမည်။

အုပ်စုဖွဲ့ဒေတာအတွက် ဂဏန်းသင်္ချာဆိုလိုသည်။

အုပ်စုဖွဲ့ထားသောဒေတာအားဖြင့်၊ ကျွန်ုပ်တို့ဆိုလိုသည်မှာ ဒေတာကို အုပ်စုများ သို့မဟုတ် ကြားကာလများအဖြစ် ဖွဲ့စည်းထားပါသည်။ ကိန်းဂဏန်းနမူနာအရွယ်အစားသည် အလွန်ကြီးမားသောအခါတွင် ၎င်းသည် များသောအားဖြင့် ဖြစ်ပေါ်သည်။

ထို့ကြောင့် ဂဏန်းသင်္ချာ၏ ပျမ်းမျှတွက်ချက်မှုသည် သဘောတရား တူညီသော်လည်း ဒေတာများကို တစ်စုတစ်စည်းတည်း စုထားသောအခါ အနည်းငယ်ကွဲပြားပါသည်။

ကြားကာလများအဖြစ် အုပ်စုဖွဲ့ထားသော ဒေတာများ၏ ဂဏန်းသင်္ချာပျမ်းမျှကို တွက်ချက် ရန်၊ အုပ်စုတစ်ခုစီ၏ အတန်းရမှတ်ကို ၎င်း၏ absolute frequency ဖြင့် မြှောက်ပြီး absolute frequencies အားလုံး၏ sum ဖြင့် ပိုင်းခြားရပါမည်။

$\displaystyle\overline{x}=\frac{\sum_{i=1}^N x_i\cdot f_i}{\sum_{i=1}^N f_i} =\frac{x_1\cdot f_1+ x_2\cdot f_2+\dots +x_N\cdot f_N}{N}$

မှတ်ချက်- ကြားကာလတစ်ခု၏ အတန်းရမှတ်ကို ကြားကာလ၏ အဆုံးမှတ်များ၏ ပေါင်းလဒ်ကို နှစ်ချက်ခွဲ၍ တွက်ချက်သည်။ ဥပမာ၊ ကြားကာလ [3,7) ၏ class note သည်-

$\cfrac{3+7}{2}=5$

၎င်းကို မည်သို့လုပ်ဆောင်သည်ကို သင်မြင်နိုင်စေရန်၊ အောက်တွင် ကြားကာလများအဖြစ် အုပ်စုဖွဲ့ထားသော ဂဏန်းသင်္ချာပျမ်းမျှအပေါ် ဖြေရှင်းထားသော လေ့ကျင့်ခန်းတစ်ခုဖြစ်သည်။

ကျွန်ုပ်တို့သည် အုပ်စုတစ်စု၏အလေးချိန်ကို ကိန်းဂဏန်းစာရင်းအင်းလေ့လာလိုသည်၊ ဤအတွက်ကြောင့် လူ 81 ဦးရှိသော ကိုယ်စားလှယ်အဖွဲ့ကို ကျွန်ုပ်တို့တွေ့ဆုံမေးမြန်းခဲ့ပြီး အောက်ပါအချက်အလက်များကို ရရှိခဲ့ပါသည်။

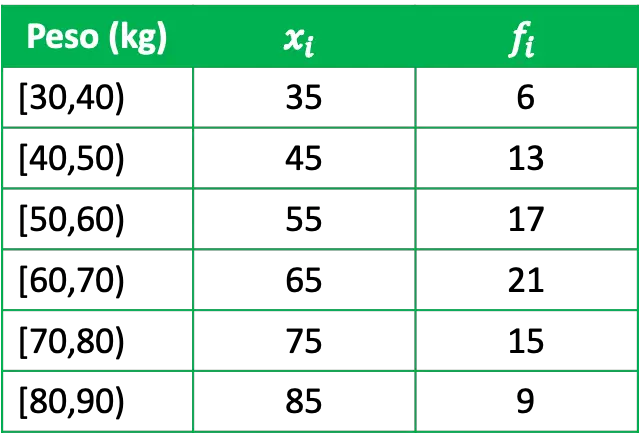
x _i သည် အုပ်စုတစ်ခုစီ၏ အတန်းရမှတ်ဖြစ်ပြီး f _{i သည်} ၎င်း၏ absolute frequency ဖြစ်ပြီး၊ ဆိုလိုသည်မှာ ဤကြားကာလတွင် ကိုယ်အလေးချိန်ရှိသူများ အရေအတွက်ကို ဆိုလိုသည်။

ဂဏန်းသင်္ချာဆိုလိုရင်းကို ဆုံးဖြတ်ရန်အတွက်၊ ၎င်းတို့၏ သက်ဆိုင်ရာ ကြိမ်နှုန်းအလိုက် အတန်းမှတ်စုများ၏ ရလဒ်ဖြစ်သည့် ကြိမ်နှုန်းဇယားတွင် ကော်လံတစ်ခုကို ထည့်ရန် လိုအပ်သည်-

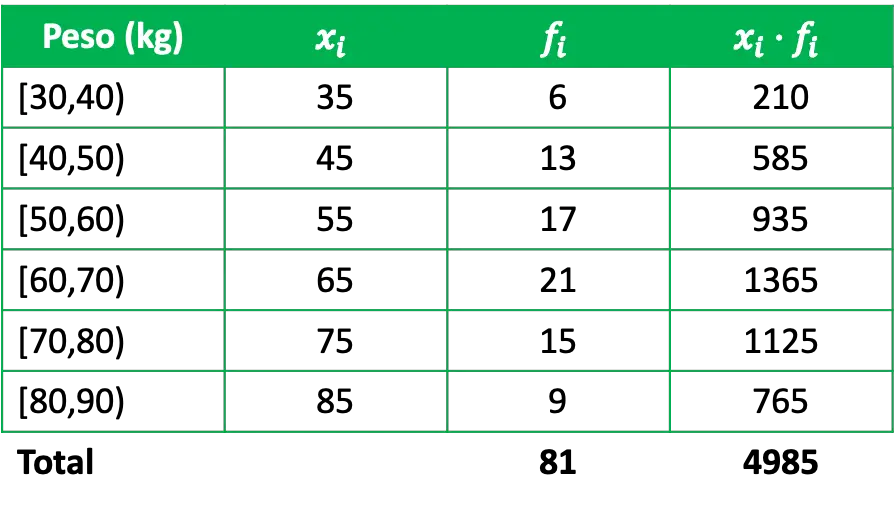
အုပ်စုဖွဲ့ဒေတာအတွက် ဖြေရှင်းထားသော ဂဏန်းသင်္ချာဆိုလို လေ့ကျင့်ခန်း

ထို့ကြောင့် အုပ်စုဖွဲ့ဒေတာ၏ ဂဏန်းသင်္ချာပျမ်းမျှကို တွက်ချက်ရန်၊ အတန်းမှတ်စုများ၏ ထုတ်ကုန်များ၏ ပေါင်းလဒ်ကို ဒေတာစုစုပေါင်းအရေအတွက်ဖြင့် ၎င်းတို့၏ကြိမ်နှုန်းများဖြင့် ပိုင်းခြားပါ။

$\displaystyle\overline{x}=\frac{\sum_{i=1}^N x_i\cdot f_i}{\sum_{i=1}^N f_i} =\frac{4985}{81}=61,54 \text{ kg}$

ဂဏန်းသင်္ချာ၏ ဂုဏ်သတ္တိများ

ဂဏန်းသင်္ချာပျမ်းမျှတွင် အောက်ပါလက္ခဏာများရှိသည်။

ပျမ်းမျှထံမှ ဖြန့်ဖြူးမှုတစ်ခုရှိ ဒေတာအားလုံး၏ သွေဖည်မှုပေါင်းလဒ်သည် သုညဖြစ်သည်။

$\sum_{i=1}^N\left(x_i-\overline{x}\right)=0$

နမူနာတစ်ခုရှိ ဒေတာအားလုံးတွင် တူညီသောပမာဏကို ထည့်ပါက၊ နမူနာသည် ထိုပမာဏဖြင့် တိုးလာသည်ဟု ဆိုလိုသည်။

နမူနာတစ်ခုတွင် တန်ဖိုးအားလုံးကို ကိန်းတစ်ခုဖြင့် မြှောက်ပါက၊ နမူနာဆိုလိုရင်းကို ထိုဂဏန်းဖြင့် မြှောက်သည်။

ဂဏန်းသင်္ချာပျမ်းမျှအား အရေအတွက်ကိန်းရှင် များတွင်သာ တွက်ချက်နိုင်သည်။ တစ်နည်းဆိုရသော် သင်သည် အရည်အသွေးရှိသော ကိန်းရှင်များ၏ ပျမ်းမျှအား မယူနိုင်ပါ။

ဂဏန်းသင်္ချာဆိုလိုသည်မှာ ဖြန့်ဖြူးမှုတစ်ခု၏ အနိမ့်ဆုံးနှင့် အများဆုံးကြားရှိ တန်ဖိုးတစ်ခုဖြစ်သည်။

$\text{min}\{x_1,x_2,...,x_N\}\leq \cfrac{x_1+\dots +x_N}{N}\leq \text{max}\{x_1,x_2,...,x_N\}$

ဤပျမ်းမျှအမျိုးအစားသည် အလွန်မြင့်မားသော သို့မဟုတ် အလွန်နိမ့်သောတန်ဖိုးများအတွက် အလွန်အထိခိုက်မခံသောကြောင့် ဂဏန်းသင်္ချာပျမ်းမျှရလဒ်ကို သိသိသာသာပြောင်းလဲသွားစေပါသည်။

ဒေတာအတွဲတစ်ခု၏ ဂဏန်းသင်္ချာပျမ်းမျှသည် တူညီသောဒေတာအစု၏ ဂျီဩမေတြီပျမ်းမျှထက် အမြဲတမ်း ညီမျှ သို့မဟုတ် ပိုကြီးသည်။

$\displaystyle\frac{x_1+x_2+\dots+x_N}{N}\geq \sqrt[N]{x_1+x_2+\dots+x_N}$

Excel ဖြင့်ဂဏန်းသင်္ချာပျမ်းမျှတွက်ပါ။

Excel တွင် ဂဏန်းသင်္ချာပျမ်းမျှတွက်ချက်ခြင်းသည် အလွန်ရိုးရှင်းသောကြောင့်၊ သင်သည် စာရွက်ပေါ်တွင် ဒေတာထည့်ရန်နှင့် AVERAGE လုပ်ဆောင်ချက်ကို အသုံးပြုရသောကြောင့် ဖြစ်သည်။

ဥပမာအားဖြင့်၊ ကျွန်ုပ်တို့ရှင်းပြသော ပထမဖြေရှင်းထားသော လေ့ကျင့်ခန်းမှ ဒေတာများ၏ ဂဏန်းသင်္ချာပျမ်းမျှအား ဆုံးဖြတ်ရန်၊ ဒေတာအားလုံးကို Excel စာရွက်စာတမ်းတစ်ခုထဲသို့ ကူးယူပြီး ဆဲလ်တစ်ခုအတွင်း အောက်ပါဖော်မြူလာကို ရေးပါ- =AVERAGE(9;7;5;8;7 ၊၅) ။ လုပ်ဆောင်ချက်သည် 7.3 ဖြစ်သည့် ဒေတာ၏ ဂဏန်းသင်္ချာပျမ်းမျှကို ပြန်ပေးပါမည်။

အထူးသဖြင့် နမူနာအရွယ်အစား အလွန်ကြီးမားသောအခါတွင် လက်ဖြင့် တွက်ချက်ခြင်းထက် Excel ပရိုဂရမ်ရှိ အချို့သောဂဏန်းများ၏ဂဏန်းသင်္ချာဆိုင်ရာ ဂဏန်းသင်္ချာပျမ်းမျှကို ရှာတွေ့ရန် ပိုမိုမြန်ဆန်ကြောင်း သိသာထင်ရှားပါသည်။

စာရေးသူအကြောင်း

Benjamin Anderson

မင်္ဂလာပါ၊ ကျွန်ုပ်သည် အငြိမ်းစား စာရင်းအင်း ပါမောက္ခ ဘင်ဂျမင်ဖြစ်ပြီး သီးသန့် Statorials ဆရာအဖြစ် လှည့်ပတ်ပါသည်။ စာရင်းဇယားနယ်ပယ်တွင် ကျယ်ပြန့်သောအတွေ့အကြုံနှင့် ကျွမ်းကျင်မှုနှင့်အတူ၊ Statorials မှတစ်ဆင့် ကျောင်းသားများကို ခွန်အားဖြစ်စေရန်အတွက် ကျွန်ုပ်၏အသိပညာကို မျှဝေလိုပါသည်။ ပိုသိတယ်။